
- •1. Розробка політики запровадження податку на викиди двоокису вуглецю для захисту озонового шару стосується:
- •2. Початкову криву виробничих можливостей суспільства показано на рисунку суцільною лінією, а нову – пунктирною.
- •3. Яке з положень є хибним?
- •4. Яке з тверджень є не відповідає дійсності?
- •5. Якщо економіка рухається вздовж квм зліва направо, то:
- •8. Крива виробничих можливостей має обов’язково лінійний характер:
- •9. Альтернативні витрати – це:
- •10. Установіть відповідність між наведеними благами та їх видами в економічній теорії:
- •Задачі Бюджетне обмеження
- •Якщо Ви витратите весь свій дохід на товар y, скільки Ви зможете його придбати?
- •Уподобання індивіда
Уподобання індивіда
Задача
8.
Споживач полюбляє яблука (х) і банани
(у). За останній рік він купив споживчий
набір із 20 кг яблук і 5 кг бананів, який
належить множині його споживчих наборів,
що задається рівнянням
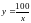 .
Цей споживач байдужий між набором
.
Цей споживач байдужий між набором
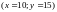 і
множиною благ, що задається рівнянням
і
множиною благ, що задається рівнянням
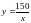 .
.
Завдання:
Побудуйте криві байдужості, що проходять відповідно через точки
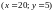 і
.
і
.Заштрихуйте набори товарів, якім споживач віддає перевагу у порівнянні з набором
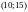 ;
заштрихуйте набори товарів, для яких
покупець віддає перевагу набору
;
заштрихуйте набори товарів, для яких
покупець віддає перевагу набору
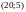 .
.Для кожного з наступного тверджень щодо переваг споживача, визначте вірне воно чи хибне:
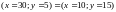 ;
; ;
;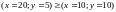 ;
;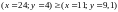 ;
;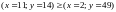 .
.
Множина є випукла, якщо лінія, проведена через будь-які дві точки цієї множини, також належить цій множині. Чи є множина наборів товарів, яким споживач віддає перевагу перед набором , випуклою множиною? Чи є множина наборів товарів, для яких споживач віддає перевагу набору випуклою множиною?
Крива байдужості споживача - . Визначити граничну норму заміщення у точках
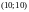 ,
,
 ,
.
Чи має дана крива байдужості спадну
граничну норму заміщення?
,
.
Чи має дана крива байдужості спадну
граничну норму заміщення?
Задача
9.
Споживач купує лише горіхи й ягоди.
Крива байдужості для споживача задається
функцією
 ,
якій належить набір
,
якій належить набір
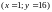 ,
а його кривій байдужості
,
а його кривій байдужості
 належить набір
належить набір
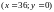 ,
де
,
де
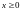 ,
,
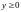 .
.
Завдання:
побудувати обидві криві байдужості споживача;
заштрихувати множину товарних наборів, яким віддає перевагу споживач у порівнянні з набором . Чи є ця множина випуклою? Заштрихувати множину наборів товарів, для якої віддається перевага набору ;
визначити нахили кривої байдужості у точках
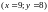 і
і
 ;
;обчислити нахили кривої байдужості у точках
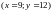 і
і
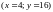 ;
;чи мають криві байдужості споживача спадну граничну норму заміщення?
Задача 10. Покупець знаходиться біля торгівельного автомату з водою у жарку і суху погоду. Машина видає одну пляшку води лише за 2 монети по 25 копійок й 1 по 10 копійок. Жодна інша комбінація монет не дозволить отримати воду з автомата. Чим більше споживач придбає води, тим краще він зможе втамувати спрагу.
Завдання:
побудувати криві байдужості для цього споживача в системі координат: х – кількість монет по 25 копійок, у – кількість монет по 10 копійок при купівлі однієї і двох пляшок води;
чи має споживач випуклі уподобання і точку насолоди?
чи завжди споживач віддає перевагу більшій кількості монет замість меншої?
якщо покупець може придбати воду в магазині, що знаходиться поруч (за будь-яку комбінацію монет) за ціною 4 копійки за одну склянку, то як будуть виглядати його кривій байдужості у тій же системі координат, який вони матимуть нахил?
Задача 11. Один зі студентів ненавидить вивчати економіку й історію. Чим більше часу він витрачає на вивчення кожного предмету, тим менше це приносить йому задоволення. Але цей студент має строго випуклі уподобання.
Завдання:
намалюйте ескіз кривої байдужості для споживача, де х – час на тиждень, що витрачається ним на вивчення економіки, у - на вивчення історії. Нахил кривої байдужості буде позитивний чи негативний?
нахил уздовж кривої байдужості студента зліва направо буде крутішим чи пологішим?
Задача 12. Студентка полюбляє витрачати час на навчання і відпочинок. Її криві байдужості в системі координат: х – час, витрачений на навчання й у – час, витрачений на відпочинок представлені концентричними колами навколо її улюбленої комбінації (точки насолоди) – 20 годин навчання і 15 годин відпочинку на тиждень. Чим ближче вона до своєї улюбленої комбінації, тим більше вона задоволена.
Завдання:
якій комбінації вона віддасть перевагу: 25 годин навчання і 3 години відпочинку чи 30 годин навчання і 8 годин відпочинку на тиждень (Порада: згадайте формулу відстані між двома точками на площині).
намалюйте криві байдужості для студентки з урахуванням її переваг щодо двох попередніх комбінацій часу.
Задача 13. Викладач завжди проводить два модулі в своєму курсі з менеджменту. Він завжди використовує лише найвищу з двох оцінок, коли визначає підсумкову оцінку.
Завдання:
студент бажає отримати найвищу оцінку за цей курс. Нехай х – його оцінка за перший модуль, у – за другий. Якій комбінації оцінок (за 100-бальною системою) студент віддасть перевагу -
 чи
чи
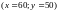 ?
?на графіку побудуйте криву байдужості, яка показує всі комбінації оцінок з менеджменту, якім студент надає таку ж перевагу, як і оцінкам . Також побудуйте криву байдужості, яка показує переваги студента такі ж, як і при оцінках
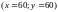 .
Чи має студент випуклі переваги для
цих комбінацій?
.
Чи має студент випуклі переваги для
цих комбінацій?студент навчається і в іншого викладача з маркетингу, який за результатами двох модулів в якості підсумкової оцінки виставляє найнижчу оцінку за модуль. Нехай х – його оцінка з маркетингу за перший модуль, у – за другий. Якій комбінації оцінок (за 100-бальною системою) студент віддасть перевагу - чи ?
на графіку побудуйте криву байдужості, яка показує всі комбінації оцінок з маркетингу, якім студент надає таку ж перевагу, як і оцінкам . Також побудуйте криву байдужості, яка показує переваги студента такі ж, як і при оцінках . Чи має студент випуклі переваги для цих комбінацій?
Задача 14. Споживачка полюбляє купувати 2 товари – грейпфрути (х) й авокадо (у).
Завдання:
нахил кривої байдужості через будь-яку точку, де споживачка має більше грейпфрутів, ніж ананасів дорівнює -2. Це означає що коли вона має більше х, ніж у, вона бажає обміняти __?__ грейпфрутів на 1 авокадо.
нахил кривої байдужості через будь-яку точку, де споживачка має менше грейпфрутів, ніж ананасів дорівнює
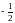 .
Це означає що коли вона має менше х, ніж
у, вона бажає обміняти __?__
грейпфрутів на 1 авокадо.
.
Це означає що коли вона має менше х, ніж
у, вона бажає обміняти __?__
грейпфрутів на 1 авокадо.на графіку побудуйте криві байдужості для даної споживачки, які проходять через точки
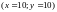 і
і
 відповідно;
відповідно;чи має споживачка випуклі уподобання?
Задача 15. Сім’я мандрівників намагається вирішити, що приготувати на обід. Дитина сказала, що її уподобання розташовується у наступному порядку (від найбільш до найменш бажаної): консерви (х), хліб (у), вода (z). Мати зробила свій вибір - хліб (у), вода (z), консерви (х). Батько ранжував свої переваги - вода (z), консерви (х), хліб (у). Вони вирішили взяти кожну пару альтернатив і шляхом рішення більшістю голосів визначити сімейні уподобання.
Завдання:
батько запропонував першими розглянути х та у, після чого обрати серед переможця й z. Яка альтернатива буде обрана?
мати запропонувала замість цього розглянути х та z, після чого переможця й у. Який вибір буде зроблений?
який порядок голосування має запропонувати дитина, щоб отримати свою улюблену страву на обід?
чи є колективні уподобання сім’ї транзитивними?
