14

Лабораторная работа №1.

«Динамика численности популяций».

Моделирование динамики популяции с помощью расчетной программы

Цель работы: Изучить модели динамики численности популяции с помощью расчетной программы.

К работе допущен

Работу выполнил

Работу защитил

2012г.

1 ТЕОРЕТИЧЕСКОЕ ВВЕДЕНИЕ

Согласно определению известного русского эколога С.С.Шварца, популяция – это элементарная группировка организмов определенного вида, обладающая всеми необходимыми условиями для поддержания своей численности длительное время в постоянно изменяющихся условиях среды.

Популяции, как и любой биологической открытой системе, свойственны определенная структура, рост, развитие, устойчивость к абиотическим и биотическим факторам.

Наиболее важным показателем благополучия популяции (устойчивости), ее роли в функционировании природной экосистемы является ее численность.

Численность популяции определяется в основном двумя явлениями – рождаемостью и смертностью, а также миграцией.

Рождаемость - количество новых особей, появившихся в единицу времени в результате размножения. В процессе размножения число особей возрастает, теоретически она способна к неограниченному росту численности.

Существуют различные типы изменения численности особей в популяции в зависимости от времени (динамики популяции).

1. Экспоненциальный рост численности.

В данной модели предполагается неограниченное количество природных ресурсов, доступных особям популяции, и отсутствие каких-либо сдерживающих факторов для роста численности. При таких допущениях численность особей в популяции возрастает по степенной зависимости, т.е. очень быстро и неограниченно.

Если обозначить через n₀ количество особей в популяции и начальный момент времени (t₀), а через N_t количество особей в некоторый момент времени t (t>t₀).

₍₁₎

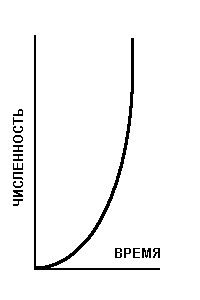
Формула (1) описывает экспоненциальную модель роста популяции, которая в графическом виде имеет форму кривой (рис.1). Экспоненциальная модель роста отвечает условиям неограниченного роста численности особей в популяции.

Рис. 1. Экспоненциальная кривая роста численности особей в популяции

2. Модель логистического роста

Максимальный размер популяции, который экосистема способна поддерживать неопределённо долго при неизменных природных условиях, называется ёмкостью экосистемы для данного вида.

Изменение численности популяции - это соотношение между биологическим потенциалом (прибавление особей) и сопротивлением среды (гибелью особей, смертностью). Факторы сопротивления среды ведут к увеличению смертности, и кривая численности выходит на плато или даже идет вниз, если популяционный взрыв вызвал истощение жизненно важных ресурсов экосистемы. Кривая роста численности популяции при сопротивлении среды приобретает S-образный вид (рис. 2).

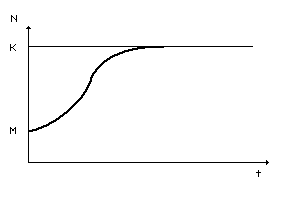
Рис. 2. Модель S-образного роста численности популяции

Таким образом, в естественных условиях неограниченный рост невозможен и рано или поздно численность популяции достигнет своего предела, который определяется ёмкостью среды (пространственной, пищевой и т.д.). Если обозначить через максимально возможное число особей в популяции некоторую величину К (ёмкость среды) и ввести поправочный показатель, учитывающий "сопротивление" среды росту численности в виде отношения:

(8)

где а - константа интегрирования, определяющая положение функции относительно начала координат, она может быть найдена из выражения (при условии, r=const).

(9)

Выражение (8) описывает так называемую кривую логистического роста (рис.2).

3. Периодический (дискретный) рост

Когда популяция под действием сопротивления среды перестает расти (экспоненциальный рост сменяется s-образным), ее численность обнаруживает тенденцию к колебаниям относительно верхнего уровня роста. Подобные колебания численности могут быть случайными и периодическими (сезонными, многолетними). Такие колебания численности называются периодической динамикой численности популяции (рис.3).

Существуют ряд причин, вызывающих колебания численности: влияние абиотических факторов, недостаток пищи, внутрипопуляционных и межпопуляционных конкурентных отношений, выедание хищниками, болезни и пр.

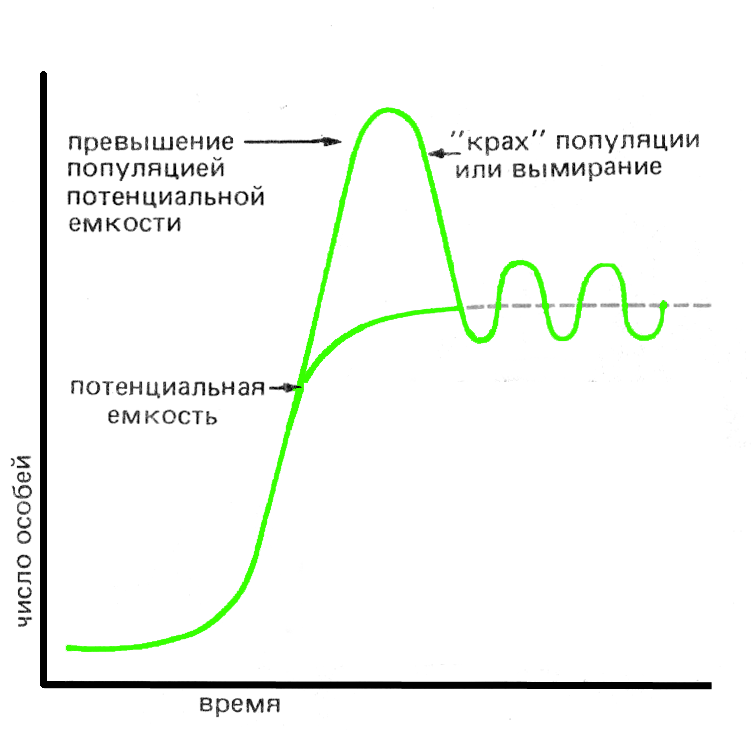
Экологи выделяют два основных типа колебаний численности популяции и множество промежуточных вариантов (рис.3,4,5).

При первом типе периодические нарушения среды, такие как пожары, наводнения ураганы и засухи, часто приводят к катастрофической, не зависящей от плотности популяции, смертности. Так, популяции однолетних растений и насекомых быстро растут летом, а с наступлением холодов резко сокращаются.

Рис. 3 Колебания численности популяции вокруг ёмкости

Популяции, рост которых дает регулярные или случайные всплески, называются оппортунистическими. Такой тип динамики характерен для ряда беспозвоночных, рыб и некоторых млекопитающих (грызунов, зайцеобразных). Колебания

численности этих популяций управляется абиотическими факторами.

Другие популяции, так называемые равновесные (свойственные многим позвоночным), обычно находятся в состоянии, близком к состоянию равновесия с ресурсами, значения их плотности гораздо более устойчивы. Преобладание в экосистеме видов с тем или иным типом динамики зависит от степени сложности, следовательно, устойчивости экосистемы. В простых по структуре экосистемах, которые подвергаются воздействию физических стрессов либо необычных или нерегулярных факторов (арктические пустыни, тундра, высокогорье, пустыни, вновь возникшие водоемы и т.п.), численность популяции зависит от погодных условий, химических загрязнений и т.п. В стабильных экосистемах, имеющих сложную структуру или не подверженных физическим стрессам (леса, озера, степи), регуляция численности осуществляется за счет биологических факторов. В ходе сукцессии экосистемы как правило наблюдается закономерная смена оппортунистических пионерских популяций популяциями с равновесным, устойчивым типом динамики.

Коллапс популяции возникает, когда численность популяции превысит ёмкость экосистемы или когда изменения условий окружающей среды внезапно понижают ёмкость экосистемы.

Разностный аналог уравнения логистической кривой имеет вид:

В зависимости от величины параметра r и его соотношения с величиной К отмечаться несколько вариантов кривых роста численности (рис. 5).

При 0 < r< 1 наблюдается монотонное приближение численности к максимально возможной.

При 1 < r < 2 имеют место затухающие колебания.

При 2 < r < 2,53 кривая будет представлена двухточечными циклами.

При 2,53 < r < 3,1 получаются циклы большей длины, чем в предыдущем случае.

При r > 3,1 отмечается нерегулярное поведение кривой.