Переменная vаr1, экспоненциальное распределение

Значение критерия Колмогорова-Смиронова: d=0,1345275

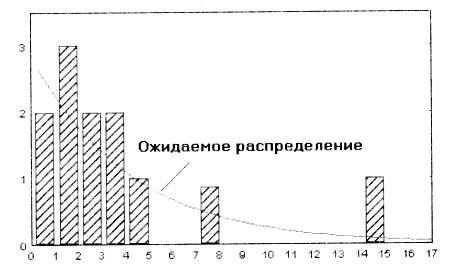
Рис. 1.7

Приведем основные формулы для расчетов CMO вида M/M/m [7].

1. Вероятность того, что все устройства обслуживания свободны,

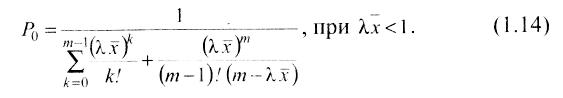
2. Вероятность того, что занято обслуживанием k-е устройство или в системе находится k требований,

3. Вероятность того, что все устройства заняты (k≥m ). Обо­значим эту вероятность через π :

4. Вероятность того, что все устройства заняты обслуживанием и s требований находятся в очереди,

5. Вероятность того, что время пребывания требований в очере­ди превышает некоторую величину t,

6. Средняя длина очереди

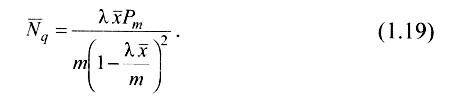
7. Среднее количество свободных от обслуживания устройств

8. Среднее количество занятых обслуживанием устройств

9. Среднее время ожидания требованием начала обслуживания в системе

Приведенные формулы позволяют выполнять расчеты для CMO вида M/M/m и сравнивать их c полученными результатами имитаци­онного моделирования.

Глава 2. Вероятностные сети систем массового обслуживания

2.1. Общие сведения о сетях

В общем случае сеть CMO можно представить в виде графа, вершинами которого являются одноканальные и многоканальные CMO (дуги определяют потоки передачи требований).

Простейшая разомкнутая или открытая сеть получается при по­следовательном соединении CMO (рис.2.1). Она еще называется многофазной CMO.

Рис. 2.1

Различают замкнутые и разомкнутые сети. Для замкнутой веро­ятностной сети не существует внешних источников требований, то есть в ней всегда находится одно и то же количество требований. Для разомкнутой сети имеются источники требований и стоки требований.

Простейшая замкнутая сеть показана на рис. 2.2. Эта система c отказами и восстановлениями хорошо известна из теории массового обслуживания. В системе постоянно находятся М1 требований, кото­рые появляются при отказе устройств M. Если устройство отказало, то поступает требование на его ремонт к бригаде c N ремонтниками, которые ремонтируют устройство, а потом отремонтированное уст­ройство восстанавливает свою работу. На рис. 2.2 это показано об­ратной связью от N₁ устройств. Сеть также используется при модели­ровании компьютерной системы, которая работает в режиме «запрос – ответ», то есть пользователь не посылает новый запрос к системе до тех пор, пока не получит ответ на предшествующий запрос. За­просы обрабатываются любым из N1 компьютеров. Примерами таких систем могут быть автоматизированные системы продажи билетов на поезда или самолеты, системы передачи транзакций от кассиров в банке и т. п.

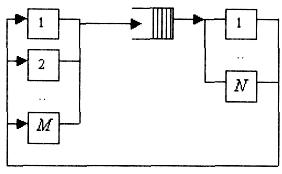
Рис. 2.2

Сеть (рис. 2.3) содержит K узлов и N требований, которые нахо­дятся в сети. Каждый узел может иметь одно или несколько одинако­вых устройств обслуживания. C вероятностью (или частотой) q_0j – тре­бования поступают к любому узлу сети, a c вероятностью q_kj (j = 1,..., К) требование, которое оставляет узел k, направляется к узлу j. Таким образом, любое требование до завершения своего обслужи­вания в сети обычно проходит несколько узлов.

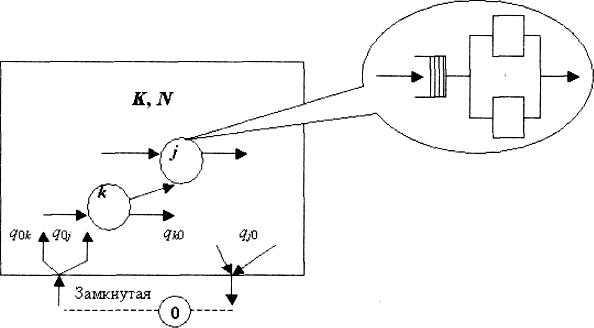
Рис. 2.3

Внешняя среда обозначается как узел 0 сети. Если сеть замкну­тая, то требования c выхода направляются на вход (рис. 2.3, пунктир­ная линия) и количество требований N в сети не изменяется.

Для потоков требований в сети справедливы законы о суммар­ных потоках, которые показаны на рис. 2.4, 2.5, при условии, что сеть работает в установившемся режиме.

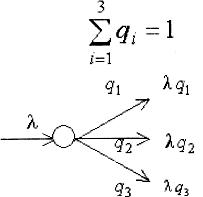
Рис. 2.4

Рис. 2.5

Для расчетов сетей массового обслуживания используется тео­рия вероятностных сетей, которая основывается на марковских и по­лумарковских процессах [8], но большинство результатов получено только для экспоненциальных законов распределения. При количест­ве узлов сети больше трех для расчетов используются численные приближенные методы. Операционный анализ [9] в отличие от теории массового обслуживания опирается на логику работы рассматри­ваемой или моделируемой системы. Это позволяет установить про­стые зависимости между параметрами и показателями работы систе­мы, не абстрагируясь от процессов ее функционирования.