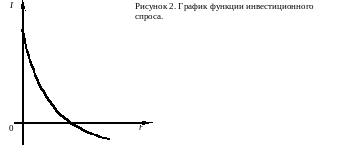- •Капитал как фактор производства
- •Движение капитала и капитальные фонды.
- •Финансовые и реальные инвестиции
- •Модель гибкого акселератора Койка.
- •1. Непрерывное время.
- •2. Дискретное время.
- •Пример 2. Модель гибкого акселератора Койка.
- •Накопление капитала и теория q Тобина как другое выражение неоклассической теории рентной цены капитала.
- •Пример 1. Оптимальный запас капитала и q Тобина.
Модель гибкого акселератора Койка.
1. Непрерывное время.
Проиллюстрируем принцип акселерации простым числовым примером [Ошибка! Источник ссылки не найден., т.1, с.246-248]. Пусть величина капитального оборудования в 10 раз превышает стоимость реализованной продукции. Допустим, объем реализации – 6 млн. руб., то есть оборудование оценивается в 60 млн. руб. Пусть оно состоит из 20 машин разного возраста, причем ежегодно изнашивается и подлежит возмещению 1 машина. Значит, инвестиции (I) составят 3 млн. руб., или 1 машину; остаток Y–I, равный 6 млн. руб. дадут в сумме заработная плата и прибыль. Пусть выпуск возрастет до 9 млн. руб., то есть на 50 процентов. В таком случае потребуется объем основного капитала (K) в размере 30 штук, или 90 млн.руб. При этом инвестиции составят I=10+1=11, что будет означать их рост на 1000 процентов.
В непрерывном времени модель гибкого акселератора (Койка) описывается линейным дифференциальным уравнением [Ошибка! Источник ссылки не найден., Ошибка! Источник ссылки не найден., Ошибка! Источник ссылки не найден.]:
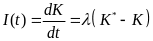 . (17)
. (17)
Это так называемая система с запаздыванием. В ней скорость изменения переменной зависит от ее отставания по отношению к своему оптимальному значению [Ошибка! Источник ссылки не найден., с.74-75]. Здесь λ – это коэффициент ускорения, или акселерации:
 .
.
Разделяем переменные в (17):
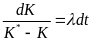 . (18)
. (18)
Поскольку
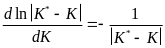 ,
можно записать
,
можно записать
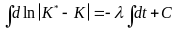 ; (19)
; (19)
а
значит, 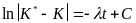 . (19.1)
. (19.1)
Потенцируем (4.45) и снимаем модуль адекватным подбором константы C1 (допуская отрицательные и нулевые значения)
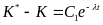 ,
или
,
или
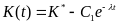 . (20)
. (20)
Определяем константу C1 по значению запаса капитала в начальный момент времени
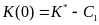 ;
;
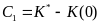 ; (20.1)
; (20.1)
В итоге траектория динамики запаса капитала такова (рис.4.3-4.4):
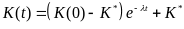 . (21)
. (21)
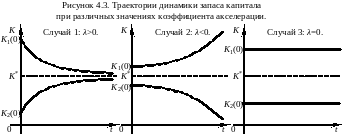
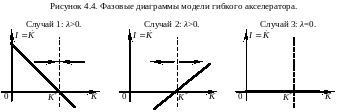
Традиционно, в силу очевидных экономических соображений, полагается, что 0<λ<1.
Подставляя полученное выражение текущего запаса капитала (21) в модель гибкого акселератора (17), можно получить траекторию динамики инвестиций во времени
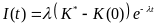 .
.
2. Дискретное время.
В дискретном
времени модель гибкого акселератора
описывается конечно-разностным
уравнением: 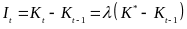 , (22)
, (22)
или 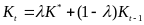 . (22.1)
. (22.1)
Выпишем
соответствующее соотношение между
запасами капитала в нулевом и первом
периодах: 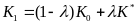 . (22.2)
. (22.2)
С учетом
(22.2) можно перейти от зависимости между
капиталом во втором и первом периодах
– к соотношению между фондами второго
и нулевого временн интервалов:
интервалов:  . (22.3)
. (22.3)
Аналогично, соотношение между запасами капитала в третьем и нулевом периодах будет выглядеть так:
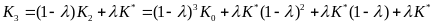 . (22.4)
. (22.4)
Соответственно, зависимость объема основных фондов в момент t от исходного запаса капитала таково REF _Ref220477857 \r :
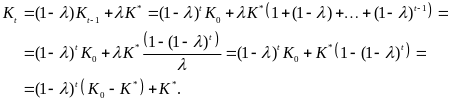 (22.5)
(22.5)
Данное решение можно получить также, используя теорию уравнений в конечных разностях REF _Ref220477857 \r :
 ;
;
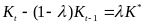 . (22.1)
. (22.1)
Решим соответствующее однородное уравнение
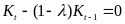 . (2)
. (2)
Распишем
соотношение (2) для всех периодов, начиная
с нулевого и кончая моментом t: 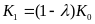 ,
,
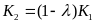 ,
,
…
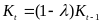 .
.
Перемножая
почленно написанные равенства, после
сокращения на произведение
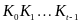 получим искомое решение однородного
уравнения [Ошибка! Источник ссылки не найден.,
с.292-294]
получим искомое решение однородного
уравнения [Ошибка! Источник ссылки не найден.,
с.292-294]
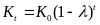 . (4)
. (4)
Проварьируем величину K0:
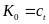 . (5)
. (5)
Уравнение
(4) приобретает вид: 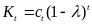 . (10)
. (10)
Подставляем (10) в исходное неоднородное уравнение (22.1):
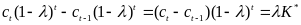 , (11)
, (11)
или 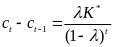 . (12)
. (12)
Суммируя
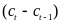 в пределах от
в пределах от
 до
до
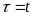 ,
получаем
,
получаем
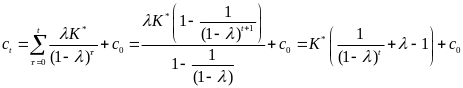 . (8)
. (8)
Подставляя
полученную таким образом неизвестную
величину
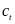 в общее решение (10) однородного уравнения
(2), получаем общее решение неоднородного
уравнения (22.1)
в общее решение (10) однородного уравнения
(2), получаем общее решение неоднородного
уравнения (22.1) 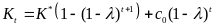 . (9)
. (9)
Определим
константу
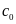 :
: 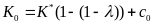 ;
;
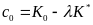 .
.
Таким образом,
как и в теории дифференциальных уравнений,
общее решение неоднородного линейного
разностного уравнения первого порядка
представляет собой сумму общего решения
соответствующего однородного уравнения
и частного решения неоднородного
уравнения: 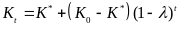 .
.
При
λ<0
и при λ>2
равновесие неустойчиво (при
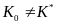 )
)
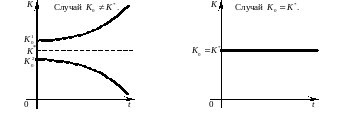
При 0<λ<2 равновесие устойчиво.

При λ=0  .
.
При λ=2  :
:
при
t=2n
;
при t=2n+1
 .
.
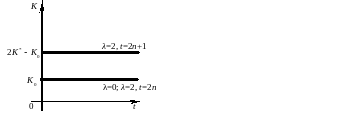
Таким образом, траектория динамики инвестиций в дискретном времени будет следующей:

Поскольку оптимальный запас капитала зависит от реальной процентной ставки (12.4), инвестиции (17), (22) так же будут являться функцией ставки процента (рис.1,2).