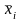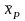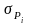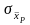8. Определение границы неисключенной систематической погрешности.

Если известно, что погрешность результата измерений определяется рядом составляющих неисключенных систематических погрешностей, каждая из которых имеет свои доверительные границы, то при неизвестных законах распределения их границы суммарной погрешности находят по формуле

,

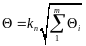где: m – число неисключенных систематических составляющих погрешностей результата измерения;

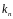- коэффициент, принимаемый равным 1,1 при доверительной вероятности Р = 0,95 и 1,4 при доверительной вероятности Р = 0,99.

8. Определение соотношения 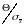. Если это соотношение меньше 0,8, то неисключенными погрешностями пренебрегают и в качестве границы погрешности результата измерения принимают . Если > 8, то пренебрегают случайной погрешностью и считают что . Если 0,8 < < 8, при определении границ погрешности 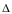следует учитывать и случайную и систематические составляющие.

1.10 Определение границы погрешности результата измерения по формуле

,

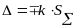где

;

.

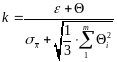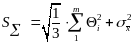1.11 Представление результата измерения и погрешности для случая симметричных доверительных границ в форме

.

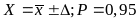2. Порядок обработки и оценка точности результатов неравноточных измерений

1. Исходными данными для обработки результатов являются:

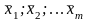- средние арифметические m рядов равноточных результатов наблюдений постоянной физической величины;

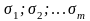- средние квадратичные отклонения результатов измерений в отдельных рядах;

- числа наблюдений в каждом ряду;

m - число рядов.

2. Вычисление значений весов по трем критериям:

«веса» Рi соответствующих групп измерений определяются из соотношения

;

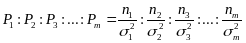"веса" P_i соответствующих групп измерений считаются обратно пропорциональными квадратам средних квадратических отклонений σ² каждой группы измерений, если количество измерений в группах неизвестно

;

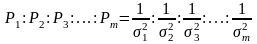весами соответствующих групп измерений считаются числа наблюдений в каждой группе, при σ = const

.

2.3 Вычисляются средние взвешенные значения

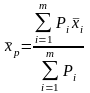
i=1,2,3…m

и отклонения от среднего по формуле

.

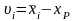4. Определяется средняя квадратичная погрешность единицы веса

.

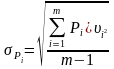5. Определяется средняя квадратичная погрешность среднего весового значения

.

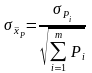5. Исходные данные и результаты вычислений сводятся в таблицу:

№№ серий	Результат	σi	ni	Рi		υi	υi²	Pi υi²
1
2
…
m

ПРИЛОЖЕНИЯ

ПРИЛОЖЕНИЕ 1

Методы

проверки нормальности распределения случайных погрешностей

Критерий согласия 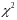(критерий Пирсона)

Идея критерия 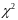состоит в контроле отклонений гистограммы экспериментальных данных от гистограммы с таким же числом интервалов, построенной на основе нормального распределения. Сумма квадратов разностей частот по интервалам не должна превышать значений 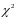, для которых составлены таблицы (приложение 3, таблица 3.6) в зависимости от уровня значимости q = 1 - Р и числа степеней свободы k = l - 3, где l - число интервалов.

Схема вычислений :

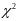1. Вычисляют среднее арифметическое значение результата измерений и среднее квадратичное отклонение по формулам:

,

.

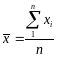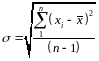2. Результаты измерений, в которых отсутствуют систематические погрешности, группируют по интервалам таким образом, чтобы эти интервалы покрывали всю ось ( - ∞, + ∞ ) и чтобы количество данных в каждом интервале было достаточно большим ( не менее 5 ).

3. Для каждого интервала 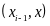подсчитывают число m_i результатов измерения, попавших в этот интервал, а затем вычисляют вероятность P_i попадания в этот интервал при нормальном законе распределения, используя формулу Лапласа (табл. 3.7 приложения 3).

.

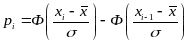4. Если в какой-либо интервал теоретически попадает меньше пяти измерений, то его соединяют с соседним интервалом. Затем вычисляют показатель разности частот

,

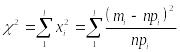где l - число всех интервалов (-∞,x), (x₁,x₂), . . . , (x_{l -1}, ∞);

n - число измерений (n = m₁+m₂+m₃+. . . +m_n).

5. Выбирают уровень значимости критерия q. Он должен быть достаточно малым, чтобы была мала вероятность отклонить правильную гипотезу.

По уровню значимости q и числу степеней свободы k ( таблица 3.6, приложения 3) находим границу критической области 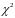, так что

p{ > } = q.

Вероятность того, что получаемое значение превышает , равна q

и мала.

Если оказывается, что 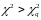, то гипотеза о нормальности отвергается.

Если , то гипотеза о нормальности принимается.

Чем меньше q , тем при том же k больше значение ,тем легче выполняется условие 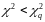и принимается проверяемая гипотеза.