4. Границя функції в точці.

Нехай функція визначена у деякому околі точки х = x₀ за винятком, хіба що, самої точки х = x₀ .

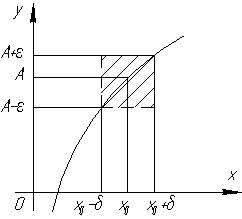
Означення. Число А називається границею функції при , якщо для довільного існує число таке, що для всіх , які задовольняють нерівність: , виконується нерівність . Пишуть: На малюнку показано: — - окіл точки ; — - окіл точки А.

Тоді геометрично це означає: що будь – якій точці з - околу відповідає деяка точка з - околу.

5. Теореми про границі.

Якщо кожна з функцій і має скінченну границю при , то справедливі формули:

1. ;

2. ;

3. ;

4. ;

5. .

6. Правила обчислення границь.

1. Якщо функція дробово – раціональна, то для знаходження границі чисельник і знаменник розкладають на множники, які потім скорочують, причому скоротитись повинен той множник, який обертається в нуль.

2. Якщо чисельник функції – стала величина, а границя знаменника дорівнює нулю, то границя такої функції є нескінченність.

3. Якщо функція містить знаки радикалів, то чисельник і знаменник помножають на вираз, спряжений до чисельника (знаменника), а потім застосовують формулу різниці квадратів. Вирази та називаються спряженими.

4. Якщо функція містить корінь третього степеня, то чисельник і знаменник помножають на неповний квадрат суми або різниці, а потім застосовують формулу суми або різниці кубів.

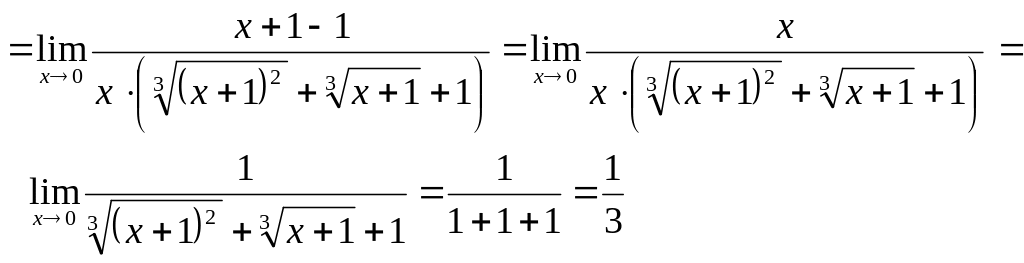
7. Границя функції на нескінченності.

Границею функції на нескінченності називається число, до якого прямує значення функції, якщо аргумент нескінченно зростає.

Розглянемо приклади:

1. Границя функції, яка представляє собою многочлен, при є не скінчен-ність.

2. Границя на нескінченності дробово – раціональної функції, у якої степінь чисельника і знаменника однакові дорівнює відношенню коефіцієнтів при старших членах.

3. Границя на нескінченності дробово – раціональної функції, у якої степінь чисельника менша за степінь знаменника, дорівнює нулю.

4. Границя на нескінченності дробово – раціональної функції, у якої степінь чисельника більша за степінь знаменника, дорівнює нескінченності.

8. Неперервність функції в точці. Дослідження функції на неперервність.

Означення. Число А називається границею функції справа при , , якщо функція визначена у правому - околі точки , і для будь – якого знайдеться таке , що для всіх , взятих з інтервалу виконується нерівність .

Позначають:

Означення. Число А називається границею функції зліва при , , якщо функція визначена у лівому - околі точки , і для будь – якого знайдеться таке , що для всіх , взятих з інтервалу виконується нерівність .

Позначають

Означення. Функція називається неперервною в точці ,якщо виконуються водночас такі умови:

• функція визначена в точці і в деякому околі цієї точки;

• існують односторонні границі і ;

• односторонні границі рівні між собою і дорівнюють значенню функції в точці .

Якщо хоча б одна з умов не виконується, функція має розрив в точці .