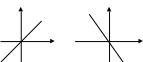Міністерство освіти і науки,молоді та спорту України

Сумський державний університет

Машинобудівний коледж

ОПОРНІ КОНСПЕКТИ

з дисципліни

“Математика”

для студентів І курсу груп денної форми навчання.

2012 р.

Рівні засвоєння навчального матеріалу:

• перший рівень – початковий – відповідь студента при відтворенні навчального матеріалу – елементарна, фрагментарна, зумовлюється початковими уявленнями про предмет вивчення;

• другий рівень – середній – студент відтворює основний навчальний матеріал, здатний розв’язувати завдання за зразком, володіє елементарними вміннями навчальної діяльності (*);

• третій рівень – достатній – студент знає істотні ознаки понять, явищ, закономірностей зв’язків між ними, а також самостійно застосовує знання в стандартних ситуаціях, володіє розумовими операціями (аналізом, абстрагуванням, узагальненням тощо), уміє робити висновки, виправляти допущені помилки; відповідь повна, правильна, логічна, обгрунтована, хоча їй бракує власних суджень (**);

• четвертий рівень – високий – знання студента є глибокими, міцними, узагальненими, системними; студент уміє застосовувати знання творчо, його навчальна діяльність має дослідницький характер, позначена вмінням самостійно оцінювати різноманітні життєві ситуації, явища, факти, виявляє і відстоює особисту позицію (***).

Розділ 1. Функції, їх властивості та графіки.

План

1. Визначення функції та способи завдання.

2. Властивості функції.

3. Графіки елементарних функцій та їх властивості. Найпростіші перетворення графіків функцій (**).

4. Границя функції в точці (*).

5. Теореми про границі (***).

6. Правила обчислення границь (***).

7. Границя функції на нескінченності (*).

8. Неперервність функції в точці. Дослідження функції на неперервність (***)

9. Контрольні питання.

10. Приклади для розв’язку.

1. Визначення функції та способи задання.

Означення. Числовою функцією з областю визна­чення D називається залежність, при якій кожному числу x із множини D (області визначення) ставиться у від­повідність єдине число y.

Записують цю відповідність так:

y = f (x).

Позначення і терміни

D (f) — область визначення;

E (f) — область значень;

x — аргумент (незалежна змінна);

y — функція (залежна змінна);

f — функція;

f (x₀) — значення функції f у точці x₀.

Область визначення функції f — це множина тих значень, яких може набувати аргумент x. Вона позначається D (f).

Область значень функції f — це множина, яка складається з усіх чисел f (x), де x належить області визначення. Її позначають E (f).

Найчастіше функцію задають за допомогою формули. Якщо відсутні додаткові обмеження, то областю визначення функції, заданої форму­лою, вважають множину всіх значень змінної, при яких ця формула має зміст.

Область визначення функції має обмеження у таких випадках:

• 

• 

• 

2. Властивості функції.

Функція зростає, якщо більшому значенню аргумента відповідає більше значення функції і спадає в іншому випадку:

f(x) ↑↔ x₂>x₁→ f(x₂)>f(x₁);

f(x) ↓↔ x₂>x₁→ f(x₂)<f(x₁);

Функція парна, якщо при зміні значення аргументу на протилежне значення функції не змінюється:

f (-x) = f(x).

Функція непарна, якщо при зміні значення аргументу на протилежне значення функції змінюється на протилежне:

f (-x) = - f(x).

Функція, що не являється непарною та парною називається функцією загального вигляду.

3. Графіки елементарних функцій та їх властивості. Найпростіші перетворення графіків функцій.

Графіком функції називається мно­жина всіх точок координатної площи­ни з координатами (x; f (x)).

№ з/п	Назва функції.	Формула.	Графік.
1.	Лінійна функція		Графік - пряма лінія
2.	Пряма пропорційність		Графік функції - пряма лінія, що проходить через початок координат
№ з/п	Назва функції.	Формула.	Графік.
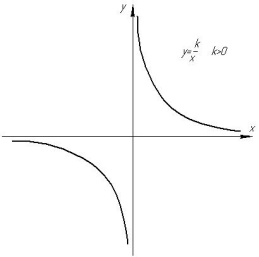
3.	Обернена пропорційність		Графік функції - гіпербола
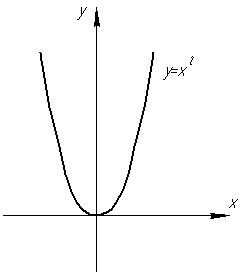
4.	Степенева функція		Графік функції - парабола.
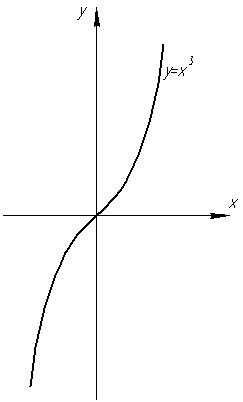
			Графік функції – кубічна парабола.
№ з/п	Назва функції.	Формула.	Графік.
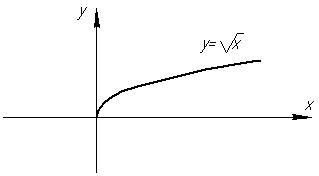
			Графік функції - вітка параболи
5.			Графік функції - кут, що утворений бісектрисами 1 та 2 чверті.

До найпростіших перетворень графіків відносяться:

№ з/п	Функція	Перетворення.
		Одержується з графіка функції зміщенням вздовж осі Оу вгору на одиниць, якщо ; вниз, якщо .
		Одержується з графіка функції зміщенням вздовж осі Ох вправо на одиниць, якщо ; вліво, якщо .
		Одержується симетричним відображенням графіка функції відносно осі Ох.
		Одержується симетричним відображенням графіка функції відносно осі Оу.
		Одержується з графіка функції розтягненням вздовж осі Оу в разів, якщо ; або стисненням до осі Ох, якщо .
		Має той самий вигляд, що й у графіка , тільки розтягнено від осі Ох, якщо , або стиснено до осі Ох, якщо .
		Ділянки графіка , які лежать праворуч від осі Оу – без зміни, і ця ж сама частина симетрично відображається відносно осі Оу.
		Ділянки графіка , які лежать вище від осі Ох – без зміни, а та частина, що нижче від осі Ох - симетрично відображається відносно осі Ох.
		Ділянки графіка , які лежать вище від осі Ох – без зміни, і ця ж сама частина симетрично відображається відносно осі Ох.