2.4 Метод авторегресії

Іноді виявляється, що значення в деякій точці часового ряду сильно корельовано з декількома передуючими і/або подальшими значеннями. Автокореляція першого порядку характеризує тісноту зв'язку між сусідніми значеннями часового ряду, автокореляція другого порядку - між віддаленими один від одного на два періоди. І взагалі, автокореляція n-го порядку відноситься до ступеня зв'язаності точок, розсіяних на n періодів. Припускаючи, що створений зв'язок між значеннями збережеться якийсь час в майбутньому, ми отримуємо механізм прогнозування, що грунтується на побудові регресії точок ряду на самих себе, тобто - авторегресії.

Авторегресійні моделі різних порядків - першого, другого, в загальному випадку n-ого - можна описати рівняннями наступного вигляду

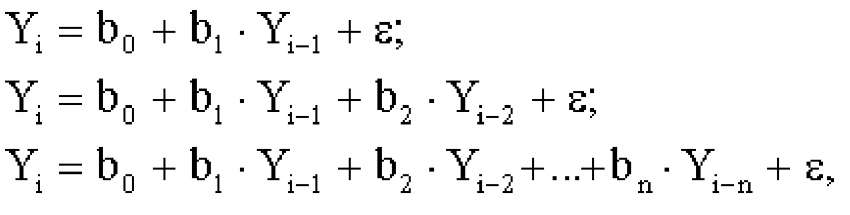
де b₀ - константа (вільний член) авторегресійного рівняння, b₀,b₁ ...b_n- коефіцієнти авторегресії,

Y_i - величина відгуку в деякий момент часу, Y_i-1,Y_i-2,...Y_i-n- відповідно відгуки одним, двома... n періодами раніше заданого, - нескорельована випадкова компонента, присутня у відгуку і пов'язана з помилками спостереження і похибками моделі.

Застосувавши даний алгоритм для таблиці прикладу 1 отримаємо наступні результати:

Таблиця 2.3

Рік	Значення Х для регресії	Обчислене значення
1993	20,1	21,228
1994	21,228	22,393
1995	22,393	23,595
1996	23,595	24,836

Рис. 2.3.Порівняльна характеристика реальних об'ємів продажу(синя лінія) і прогнозованих (червона лінія)

Для побудови надійного прогнозу нам потрібно буде вибрати кращу модель з багатьох авторегресійних, і визначення порядку цієї кращої моделі часто виявляється нетривіальною задачею, що включає розрахунок статистичних характеристик багатьох побудованих моделей і знаходження тонкого балансу між відносною простотою моделлю низьких порядків і ігноруванням в цих моделях деяких тонких взаємодій між чинниками, які можуть бути враховані тільки в складніших моделях.

Зазвичай починають з побудови моделей високих порядків, а потім поступово її спрощують, послідовно знижуючи порядок моделі. В даний час частіше поступають навпаки, починаючи з простої моделі, і при необхідності ускладнюють її.

3.Контрольні запитання

1. Що таке часовий ряд, які його основні компоненти?

2. Задачі прогнозування

3. Назвіть основні методи прогнозування

4. Метод Хольта-вінтерса

4.Лабораторне завдання

Реалізувати програмно метод Хольта-вінтерса та інший метод на вибір студента. Для довільного часового ряду побудувати прогноз за обома методами та порівняти отримані результати. При реалізації методу Хольта-вінтерса вхідними даними будуть часовий ряд та згладжувані параметри U та V, що повинні задаватись у програмі. Вихідними даними - прогнозовані дані. Далі потрібно програмно реалізувати будь-який інший метод прогнозування і побудувати прогноз. Результатом виконання лабораторної роботи повинен бути графік на якому повинна бути зображена функція вхідних даних( часовий ряд), функція отримана методом Хольта-вінтерса та функція побудована іншим довільним методом прогнозування. У висновку потрібно вказати про розбіжність зпрогнозованих функції та вхідної ( за рахунок чого виникають такі відхилення та як можна їх мінімізувати).

При захисті лабораторної роботи студент повинен знати методи прогнозування, вміти зробити необхідні зміни у тексті програми, пояснити зміст отриманих результатів.

5.ЗМІСТ ЗВІТУ