2.2 Методи Хольта і Брауна

В середині минулого століття Хольт запропонував вдосконалений метод експоненційного згладжування, згодом названий його ім'ям. У запропонованому алгоритмі значення рівня і тренда згладжуються за допомогою експоненційного згладжування. Причому параметри

згладжування у них різні.

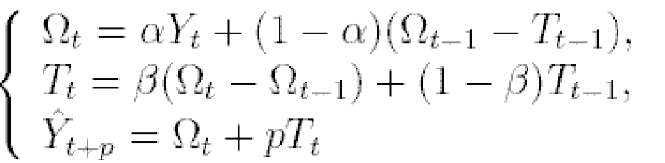
Тут перше рівняння описує згладжений ряд загального рівня.

Друге рівняння служить для оцінки тренда.

Третє рівняння визначає прогноз на p відліків за часом вперед.

Постійні згладжування в методі Хольта ідеологічно грають ту ж роль, що і постійна в простому експоненціальному згладжуванні. Підбираються вони, наприклад, шляхом перебору по цих параметрах з якимсь кроком. Можна використовувати і менш складні алгоритми в сенсі кількості обчислень. Головне, що завжди можна підібрати таку пару параметрів, яка дає велику точність моделі на тестовому наборі і потім використовувати цю пару параметрів при реальному прогнозуванні.

2.3 Метод Хольта-вінтерса

Цей метод, названий іменами його авторів, є удосконаленням методу експоненційного згладжування часового ряду. Експоненційне згладжування забезпечує наочне уявлення про тренд і дозволяє робити короткострокові прогнози, а при спробі розповсюдити прогноз на більший період -- виходять абсолютно безглузді значення: створюється враження, що розвиток процесу в сторону зростання або спадання абсолютно припинився - на будь-який період майбутнього прогнозуються одні і ті ж значення. Метод Хольта-вінтерса успішно справляється і з середньостроковими, і з довгостроковими прогнозами, оскільки він здатний виявляти мікротренди (тренди, що відносяться до коротких періодів) в моменти часу, безпосередньо передуючі прогнозним, і екстраполювати ці тренди на майбутнє. І хоча можлива тільки лінійна екстраполяція в майбутнє, в більшості реальних ситуацій її виявляється достатньо. При використанні методу необхідно послідовно обчислювати згладжені значення ряду і значення тренду, накопичені в будь-якій точці ряду.

де через E і T згладжене значення ряду і тренд, що розраховуються по всіх точкам ряду, а U і V - константи згладжування, що відносяться до оцінок рівня і тренда відповідно. Вибір значень цих констант знову-таки є суб'єктивним. З приведених рівнянь методу виходить, що значення U і V можуть знаходиться в інтервалі (0...1), але найчастіше дослідник вибирає їх значення з більш вузького діапазону [0.25 < U,V < 0.5] і при цьому значення констант не зобов'язані збігатися.

Краще всього, почати моделювання з U=V=0.3, а потім при потребі їх дещо варіювати. При вищих значеннях U в більшому ступені враховуються минулі значення ряду і тенденція розвитку процесу.

У першій точці ряду значення E1 і T1 не розраховуються, для їх розрахунку не існує попередніх експериментальних значень. У другій точці ряду приймається, що згладжене значення E2 в точності рівне спостережуваному Y2, а мікротренд за цей період вважається лінійним і розраховується як різниця між поточним і минулим значеннями T2 = Y2 - Y1. Починаючи з третьої точки вже можна користуватися вказаними вище формулами: спочатку розраховується згладжене значення E3 по згладженому значенню і мікротренду для минулої та поточної точки ряду, а потім розраховується новий мікротренд по свому попередньому значенню і різниці між минулим і лише що оціненим згладженим значенням. Потім описана процедура повторюється по всіх подальших точках часового ряду.

ПРИКЛАД 1

Таблиця 2.1.Об'єми продажу для фірми Kodak

Рік	Об’єм випуску		Коефіцієнти в рівнянні
			U =0.3; V =0.3		U=0.2; V =0.5		U=0.5; V=0.2
			E	T	E	T	E		T
1970	2.8	-		-	-	-	-	-

1971	3.0	3.000	0.200	3.000	0.200	3.000	0.200
1972	3.5	3.410	0.347	3.440	0.320	3.350	0.320
1973	4.0	3.927	0.466	3.952	0.416	3.835	0.452
1974	4.6	4.538	0.567	4.554	0.509	4.444	0.577
1975	5.0	5.032	0.516	5.012	0.484	5.010	0.569
1976	5.4	5.444	0.444	5.419	0.445	5.490	0.497
1977	6.0	5.966	0.499	5.973	0.499	5.993	0.502
1978	7.0	6.839	0.761	6.894	0.711	6.748	0.704
1979	8.0	7.880	0.957	7.921	0.869	7.726	0.923
1980	9.7	9.441	1.380	9.518	1.233	9.175	1.344
1981	10.3	10.456	1.125	10.390	1.052	10.409	1.256
1982	10.8	11.034	0.742	10.929	0.795	11.233	0.910
1983	10.2	10.673	-0.030	10.505	0.186	11471	0.133
1984	10.6	10.613	-0.051	10.618	0.150	10.952	-0.149
1985	10.6	10.588	-0.032	10.634	0.083	10.702	-0.230
1986	11.5	11.217	0.430	11.343	0.396	10.986	0.181
1987	13.3	12.804	1.240	12.988	1.020	12.234	1.034
1988	17.1	16.113	2.688	16.402	2.217	15.134	2.527
1989	18.4	18.521	2.492	18.444	2.130	18.031	2.823
1990	18.9	19.534	1.457	19.235	1.460	19,877	2.041
1991	19.4	19.877	0.677	19.659	0.942	20.659	1.034
1992	20.1	20.236	0.455	20.200	0.742	20.897	0.397

Продовження Табл. 2.1

Таблиця 2.2. Прогнозовані значення

1993	—	20.691		20.942		21.293
1994	—	21.146		21.684		21.690
1995	—	21.600		22.426		22.087
1996	—	22.055		23.167		22.484

Отже, коефіцієнти рівняння для 1970 року розраховуються як Y( рік випуску) = U =3 T₂ = Y₁ - Y₂ =3.0-2.8=0.2. Далі розраховуємо коефіцієнти для 1971 року за вищенаведеними формулами

Е3 = 0.3*(3.0+0.2)+(1-0.3)*3.5= 3.41

Т3 = 0.3*0.2+(1-0.3)*(3.41-3.0)=0.347

Далі коефіцієнти розраховують аналогічно для всіх даних в таблиці. При розрахунку прогнозу в методі Хольта-вінтерса передбачається, що згладжене значення у останній точці є опорою, а визначений для неї мікротренд збереже своє значення і в майбутньому; функція прогнозу виявляється лінійною, і тоді

де j - номер періоду в майбутньому, на який розраховується прогноз. Відповідно розрахуємо прогноз обсягу продаж на 1993 рік як Y₂₃₊₁ = E₂₃ +1* T₂₃ = 20.236 +1*0.455 = 20.691. За аналогією можна зробити аналіз і для подальших років.

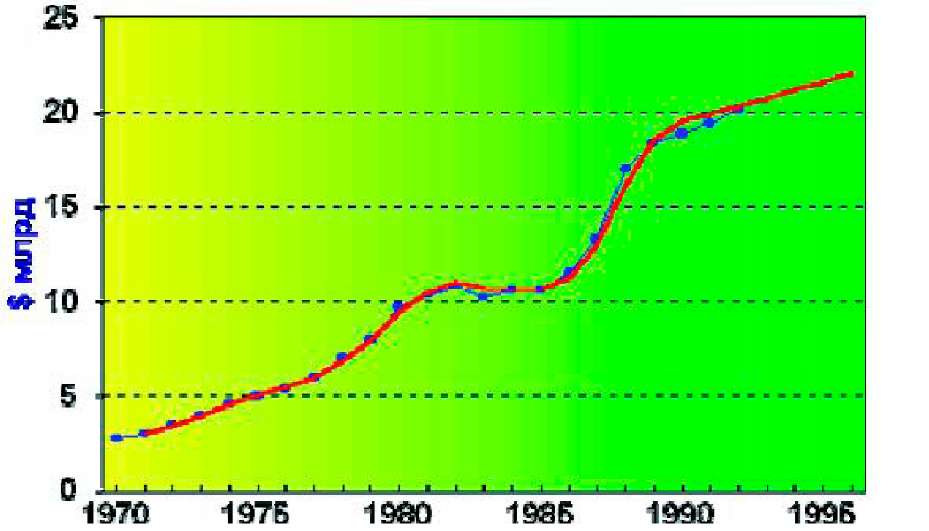
Рис. 2.2.Порівняльна характеристика реальних об'ємів продажу(синя лінія) і прогнозованих (червона лінія)

Графічне представлення результатів для випадку U = 0.3; V = 0.3 показує хорошу відповідність між згладженим і спостережуваними значеннями практично по всьому ряду, і від методу в даному випадку природно чекати хороших середньо- і довгострокових прогнозів. Оцінити ж помилку прогнозу немає можливості, оскільки неможливо побудувати статистичні характеристики моделі, порівнюючи з характеристиками моделей, побудованих регресійними методами. І хоча можна визначити залишкову суму квадратів моделі, але неможливо розрахувати дисперсію адекватності зважаючи на відсутність достовірної інформації про число мір свободи. Можна, правда, умовно прийняти, що в процесі обчислень втрачаються два ступені свободи, зв'язані коефіцієнтами U і V, і таким

чином число мір свободи на 2 менше числа точок ряду. Якщо ж не вимагати від методу зайвої строгості, подібну оцінку цілком можна використовувати.