
- •Глава 2. Линейная алгебра.
- •§1.Матрицы. Общие понятия.
- •Виды квадратных матриц (частные случаи):
- •2) Квадратная матрица вида:
- •4) Квадратные матрицы вида
- •§2. Равенство матриц. Действия над матрицами
- •I.Равенство матриц
- •II.Сложение матриц
- •Пример 2.1
- •§3. Определители
- •Пример 3.1
- •Пример 3.2
- •Миноры и алгебраические дополнения. Теорема разложения определителя по элементам строки (столбца)
- •Пример 3.3
- •Пример 3.4
- •§4. Обратная матрица
- •Правило нахождения обратной матрицы.
- •Пример 4.1
- •Пример 4.3
- •§5. Решение систем n линейных уравнений с n неизвестными матричным методом и по формулам Крамера
- •§6. Ранг матрицы.
- •Правило:
- •Пример 6.2
- •III. Элементарные преобразования. Эквивалентные матрицы.
- •IV. Базисный минор.
- •§7. Системы m линейных уравнений с n неизвестными.
- •Пример 7.1
- •Пример 7.2
- •Пример 7.3
- •§8. Метод Гаусса.
- •Пример 8.1
- •Ответ: , ,
- •§9. Однородные системы уравнений.
- •Ответ: , ,
- •§10. Линейные отображения. Преобразования координат.
- •I.Основные понятия
- •II.Преобразования координат при переходе к новому базису.
- •§11. Собственные векторы и собственные значения
Глава 2. Линейная алгебра.
§1.Матрицы. Общие понятия.
Опр. Матрицей А размера
![]() называется совокупность
чисел, расположенных в виде таблицы из
m строк и n
столбцов.
называется совокупность
чисел, расположенных в виде таблицы из
m строк и n
столбцов.
Обозначения:

Amxn; A=( ai j ), где ai j – элемент матрицы;
i=1,…,m
– номер строки (i=![]() );
);
j=1,…,n
– номер столбца (j=![]() ).
).
Замечание. Будем рассматривать числовые матрицы. Если aij – функции (или векторы), то имеем функциональную (векторную) матрицу.
Если m n , то матрица называется прямоугольной.
Если m=n , то матрица называется квадратной.
![]() – квадратная матрица порядка n.
– квадратная матрица порядка n.
Если m=1, то матрица состоит из 1-ой строки
(а1 , а2 ,…, аn) – матрица-строка.
Если n=1, то матрица состоит из 1-го столбца
![]() – матрица-столбец.
– матрица-столбец.
Примеры:
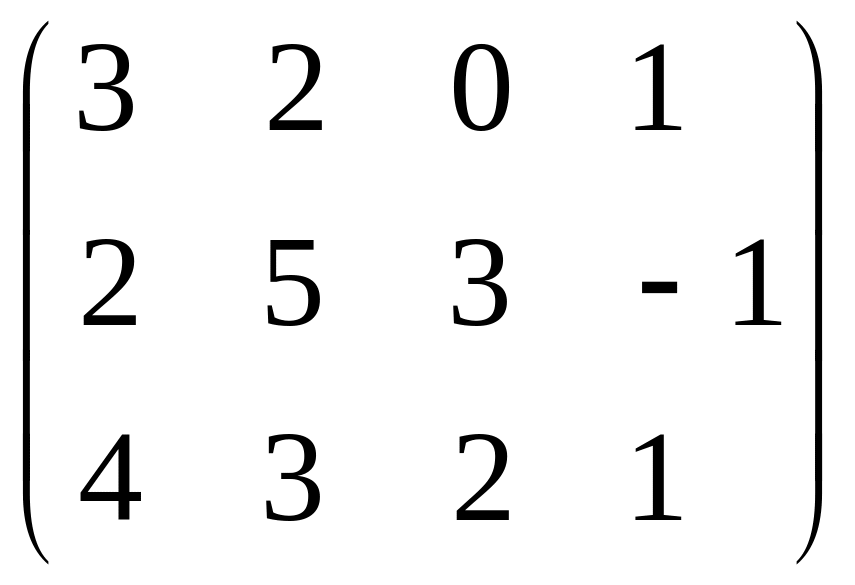 –
прямоугольная матрица размером 3х4;
–
прямоугольная матрица размером 3х4;
![]() –
квадратная матрица 2-го порядка;
–
квадратная матрица 2-го порядка;
![]() –
матрица-строка 1х4;
–
матрица-строка 1х4;
![]() –
матрица-столбец 3х1.
–
матрица-столбец 3х1.
Опр. Матрица, получаемая из данной матрицы А путем замены строк на столбцы и наоборот называется транспонированной и обозначается А* или АT.

Если А=![]() , то А называется симметричной.
, то А называется симметричной.
Виды квадратных матриц (частные случаи):
Квадратная матрица, у которой все элементы aij=0, называется нулевой матрицей
![]() .
.
2) Квадратная матрица вида:
 –
называется диагональной.
–
называется диагональной.
3) Если
![]() 1=
2=…..=
n
=1 то получим матрицу
1=
2=…..=
n
=1 то получим матрицу
 –
которая называется единичной.
–
которая называется единичной.
4) Квадратные матрицы вида
 –
–
– называются матрицами треугольного вида (А–верхняя треугольная матрица, В–нижняя треугольная матрица.)
§2. Равенство матриц. Действия над матрицами
I.Равенство матриц
Опр. Две матрицы А и В называются равными, если они имеют одинаковое число строк и одинаковое число столбцов и их соответственные элементы равны.
![]()
А=В, если
![]() .
.
II.Сложение матриц
С кладывать
можно только матрицы одинакового
размера.
кладывать
можно только матрицы одинакового
размера.
Опр. Суммой двух матриц А=(аij) и В=(bij) называется матрица С=(сij), у которой сij=aij+bij, где i=1,…,m ; j=1,…,n.
![]()
Пример 2.1
![]()
В частности, если В – нулевая матрица, то А+0=А.
Аналогично определяется разность матриц.
Сложение матриц обладает свойствами:
1)А+В=В+А (переместительный закон)
2)(А+В)+С=А+(В+С) (сочетательный закон)
3)Для любых матриц А и В одинакового размера существует единственная матрица Х такая, что А+Х=В.
Матрица Х=В–А – разность матриц. В частности, уравнение
А+Х=0 имеет единственное решение Х=0–А или Х=-А – матрица, противоположная А.
-А = (-аij).
III.Умножение матрицы на число
Опр. Произведением матрицы
А=(аij) на число к
с R
называется матрица кА = (каij),
где i=1,…,m
; j=1,…,n
![]()
Свойства
1)
![]() ;
;
![]() ;
;
![]() ,
где 0 – число, О – нулевая матрица
,
где 0 – число, О – нулевая матрица
2)
![]()
3)
![]()
4)
![]()
Пример 2.2.
![]() .
Найти 2А+Е, где Е – единичная матрица
второго порядка.
.
Найти 2А+Е, где Е – единичная матрица
второго порядка.
Решение:
![]()
IV. Умножение двух матриц
Даны матрицы:
![]() (m строк, n
столбцов)
(m строк, n
столбцов)
![]() (n строк, p
столбцов)
(n строк, p
столбцов)
Найдем произведение
![]()
Опр. Произведением матриц А
и В называется матрица С,
элементы
![]() которой равны сумме произведений
элементов i–й строки
матрицы А на соответствующие элементы
j–го столбца матрицы
В, т.е.
которой равны сумме произведений
элементов i–й строки
матрицы А на соответствующие элементы
j–го столбца матрицы
В, т.е.
![]() .
.
![]() ,
где
,
где
![]() .
.
Произведение осуществимо только в случае, когда А имеет число столбцов равное числу строк В.
Итоговая матрица
![]() имеет число строк, равное числу строк
А и число столбцов, равное числу
столбцов В.
имеет число строк, равное числу строк
А и число столбцов, равное числу
столбцов В.
В частности:
![]() .
.
Пример 2.3
 Найти
Найти
![]()
Решение:
![]()

Пример 2.4
![]() Ответ:
Ответ:
![]()
Пример 2.5
![]()
![]() .
Найти
и
.
Найти
и
![]()
Ответ:
![]() .
.
Пример 2.6

 Найти
Найти![]()
Ответ:

В общем случае
![]()
(Если
![]() ,
то матрицы А и В называются
коммутативными).
,
то матрицы А и В называются
коммутативными).
Свойства
1)
![]()
2)
![]()
3)
![]() ;
;
![]()
4) AE = EA = A, где А – квадратная матрица.
V. Умножение матрицы на матрицу-столбец.
Дано:
![]() ;
;
![]()
Найти:
![]()

 =
=![]() =
=
![]()
Пример 2.7
![]() ;
Х =
;
Х =![]() .
Найти
.
.
Найти
.
Решение:
 .
.
Пусть А – квадратная матрица
![]() или
или

При умножении квадратной матрицы на матрицу-столбец получается матрица-столбец той же высоты.
Пример 2.8
 .
.
Пример 2.9
![]()
![]() Найти
Найти![]()
Ответ:
![]()
