9.4. Перенос энергии волной
Поскольку
волна – это процесс распространения
колебаний в пространстве, а колебания
обладают энергией, то распространение
волны в каком-либо направлении в
пространстве сопровождается переносом
энергии колебаний в этом направлении.
Рассмотрим характеристики переноса
энергии волной. При распространении
волны каждый элемент объема волнового
поля будет обладать энергией. Выделим
в волновом поле элементарный объем dV.
В этом объеме будет заключена энергия
колебаний dW.
Величина
называется объемной плотностью энергии
волнового поля. Найдем эту величину.
Объем среды, в котором распространяется волна, обладает кинетической и потенциальной энергиями колебаний частиц. Выделим в среде частицу объемом ΔV и массой Δm. Ее кинетическая энергия
где
–
плотность среды,
–
скорость колебаний частицы.
Используя формулу волны (7.3). Тогда скорость частицы
а ее кинетическая энергия
Для
определения потенциальной энергии
волны заметим, что энергия упруго
деформированного элемента объемом
где
–
площадь поперечного сечения,
–
длина выделенного объема, может
быть представлена в виде U
= =
Здесь учтено, что абсолютная деформация
Δl
при сжатии или растяжении элемента
длиной Δx
равна
т.е. разности смещений концов элемента,
–
жесткость элемента. С учетом этого
получаем
(9.6)
де
– модуль Юнга,
– относительная деформация элемента
Δx,
которая при
в случае волны переходит в частную
производную от
по x:
Подставляя это в выражение (9.6) и учтя, что волновое число k = = ω/v для потенциальной энергии рассматриваемой частицы будем иметь
Поскольку при передаче энергии волновом процессе ΔK = ΔU, для фазовой скорости волны получим
(9.7)
Окончательно для потенциальной энергии частицы среды будем иметь
Полная энергия частицы
Из полученного выражения следует, что энергия волны распространяется с той же скоростью v = 2ω / 2k = ω / k, что и упругая волна, т.е. она не локализована в данном объеме, а передается посредством упругих сил от частицы к частице (эстафетный механизм распространения упругих волн). Такие волны называются бегущими волнами. Для определения энергии волны в некотором объеме V нужно проинтегрировать по этому объему. Зная энергию, определим плотность энергии:
Среднее значение плотности энергии w за период найдется как
(9.8)
В
(9.8) при переходе от первого интеграла
ко второму учтено, что
угловые скобки обозначают усреднение
по времени.
Энергия,
переносимая волной через произвольную
поверхность за единицу времени, т.е.
величина
называется потоком энергии (измеряется
в единицах мощности). Энергия, переносимая
волной за единицу времени через единичную
площадку, перпендикулярную направлению
распространения волны, называется
плотностью потока энергии волны, или,
другими словами, поток энергии волны,
проходящий через единичную площадку,
перпендикулярную направлению переноса
энергии. Обозначим плотность потока
энергии через S.
Тогда по определению
где
-
величина площади поверхности, через
которую проходит поток энергии
Измеряется плотность потока энергии в
Выразим
величину плотности потока энергии волны
через объемную плотность энергии
волнового поля. Поставим на пути волны
какую-либо поверхность
(рис.
6.). Через элемент
этой
поверхности за время dt
будет перенесена та энергия, которая
заключена в прилегающем к этому элементу
слое волнового поля толщиной vdt,
т.е. в объеме
где v
– скорость волны. Энергия, заключенная
в этом объеме,
Разделив эту величину на dt,
найдем поток энергии проходящий через
площадку за единицу времени, а разделив
затем и на
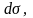найдем плотность потока энергии волны:
S = wv.
Как видим, плотность потока энергии
волны равна произведению объемной
плотности энергии волнового поля на
скорость волны. Величина w
зависит от времени, поэтому и плотность
потока S
является функцией времени.
Поскольку объемная плотность энергии есть величина скалярная, а скорость – вектор, то и плотность потока энергии волны будет величиной векторной. Поэтому полученную выше формулу для плотности потока энергии волны можно записать в векторном виде S = wv. Этот вектор был введен Н.А. Умовым и называется вектором Умова. Модуль этого вектора равен плотности потока энергии волны, а направление совпадает с направлением распространения волны (так как w > 0).
Важной характеристикой волны является величина, называемая интенсивностью волны, обозначают I. Ее определяют как среднее значение за период волны от потока энергии волны:
Следовательно, интенсивность волны равна произведению средней плотности энергии на скорость волны. Подставляя сюда выражение (9.8), для интенсивности волны будем иметь
Как видим, интенсивность волны пропорциональна квадрату ее амплитуды.