
- •Измерение физических величин и математическая обработка результатов измерений Понятие об измерении
- •Классификация измерений
- •Классификация погрешностей по закономерности проявления
- •Систематические погрешности, оценка их величины
- •Случайные погрешности прямых измерений
- •Классификация систематических погрешностей
- •Оценка случайной погрешности
- •Суммирование погрешностей
- •Погрешности косвенных измерений
- •Способ 1
- •Способ 2
- •Контрольные вопросы:
- •Лабораторная работа № 1 Измерение масс
- •Методы взвешивания
- •Определение объёма и плотности тел правильной геометрической формы, площади поперечного сечения проволок
- •Штангенциркуль
- •Порядок выполнения работы
- •Косвенные измерения объёма параллелепипеда
- •Косвенные измерения объёма цилиндра
- •Приложение Сравнение основных терминов и определений в области метрологии
- •Содержание
- •2. Физические величины 2. Физические величины
- •3. Единицы физических величин 3. Единицы физических величин
- •4. Измерения 4. Измерения физических величин
- •5. Виды средств измерений 5. Средства измерительной техники
- •Измерения
- •6. Принципы, методы и методики измерений
- •9. Погрешности средств измерений 9. Погрешности средств измерений
- •Параметры и свойства средств измерений
- •10. Условия измерений
- •Эталоны и образцовые средства измерений
- •Эталоны единиц физических величин
- •11.Понятия, относящиеся к метрологической службе
- •12. Метрологическая служба и ее деятельность
- •440026, Г. Пенза, ул. Лермонтова, 37. Корпус 5. Комн. 466.
Погрешности косвенных измерений
Теперь необходимо рассмотреть вопрос о том, как находить погрешность физической величины , которая определяется путем косвенных измерений. Общий вид уравнения измерения Y=f(Х1, Х2, … , Хn ), где Хj – различные физические величины, которые получены экспериментатором путем прямых измерений, или физические константы, известные с заданной точностью. В формуле они являются аргументами функции. В практике измерений широко используют два способа расчета погрешности косвенных измерений. Оба способа дают практически одинаковый результат.
Способ 1
Сначала находится абсолютная , а затем относительная погрешности. Этот способ рекомендуется для таких уравнений измерения, которые содержат суммы и разности аргументов. Общая формула для расчета абсолютной погрешности при косвенных измерениях физической величины Y для произвольного вида f функции имеет вид:

Для
нахождения относительной погрешности
нужно прежде всего найти среднее значение
величины Y.
Для этого в уравнение измерения надо
подставить средние арифметические
значения величин
Xj.
То есть среднее значение величины
Y
равно:

Пример: Найдем погрешность измерения объёма V цилиндра. Высоту h и диаметр D цилиндра считаем определёнными путём прямых измерений, причём пусть количество измерений n=10 . Формула для расчета объёма цилиндра, то есть уравнение измерения, имеет вид:

Тогда, после подстановки средних значений, найдём:
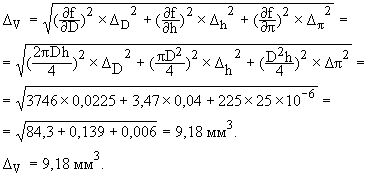
Погрешность V в данном примере зависит, как видно, в основном от погрешности измерения диаметра.

Способ 2
Этот способ определения погрешности косвенных измерений отличается от первого способа меньшими математическими трудностями, поэтому его чаще используют. В начале находят относительную погрешность , и только затем абсолютную . Особенно удобен этот способ, если уравнение измерения содержит только произведения и отношения аргументов. Порядок действий можно рассмотреть на том же конкретном примере – определение погрешности при измерении объёма цилиндра:
![]() .
.
Все численные значения входящих в формулу величин сохраним теми же, что и при расчетах по способу 1.
 .
.
При использовании способа 2 следует действовать так:
прологарифмировать уравнение измерения (логарифм берём натуральный):

заменить дифференциал каждой величины на абсолютную погрешность этой же величины, а знаки “минус”, если они есть перед погрешностями, на “плюс”:
![]() .
.
Казалось бы, что с помощью этой формулы уже можно дать оценку для относительной погрешности
 ,
однако это не так. Требуется так оценить
погрешность
,
чтобы доверительная вероятность этой
оценки совпадала с доверительными
вероятностями оценки погрешностей тех
членов, которые стоят в правой части
формулы. Для этого, чтобы это условие
выполнялось, нужно все члены последней
формулы возвести в квадрат:
,
однако это не так. Требуется так оценить
погрешность
,
чтобы доверительная вероятность этой
оценки совпадала с доверительными
вероятностями оценки погрешностей тех
членов, которые стоят в правой части
формулы. Для этого, чтобы это условие
выполнялось, нужно все члены последней
формулы возвести в квадрат:
![]()
Теперь можно вычислить относительную погрешность, извлекая корень квадратный из обеих частей уравнения:
![]()
Или в других обозначениях относительная погрешность объёма равна:
![]()
Причём вероятность этой оценки погрешности объёма будет совпадать с вероятностью оценки погрешностей, входящих в подкоренное выражение членов:
![]()
Сделав вычисления убедимся, что результат совпадает с оценкой по способу 1:
![]()
Теперь, зная относительную погрешность, находим абсолютную:
V=0,19 х 47=9,4 мм3, P=0,68.
Окончательный результат после округления имеет вид:
V = (47 + 9) мм3, V = 19%, P=0,68.
