Суммирование погрешностей

Общая абсолютная погрешность измерения  всегда содержит две составляющие: систематическую погрешность _с и случайную погрешность _сл. Можно оценить величину _с и отдельно оценить величину . Как после этого найти суммарную погрешность?

Общая абсолютная погрешность находится по формуле:

.

Пусть одна из погрешностей, например _с, в 2 раза меньше, чем другая _сл.   Тогда согласно вышеприведенной формуле:

.

Видно, что абсолютная погрешность в этом случае лишь на 10% больше, чем случайная. То есть, если бы систематической погрешности вообще не было, то в нашем примере это мало бы повлияло на общую абсолютную погрешность. Теперь учтем, что погрешность редко удается оценить с точностью лучше чем 10–20 %, тогда в нашем случае можно положить =_сл, то есть систематической погрешностью _с можно вообще пренебречь.

Из сказанного вытекают следующие правила измерений:

1. Если систематическая погрешность в два и более раз больше, чем случайная, то случайной погрешностью можно пренебречь; большое количество измерений при этом проводить нецелесообразно, так как _с не уменьшается при увеличении n. Итак, если _с _сл, то _с (при этом достаточно провести три-четыре измерения только для того, чтобы убедиться, что показания прибора повторяются без случайных отклонений).

2. Если, наоборот, случайная погрешность более чем в 2 раза превышает систематическую, то систематической погрешностью можно пренебречь, то есть если _сл_с, то _сл (желательно провести побольше измерений для уменьшения _сл).

3. Если обе составляющие общей абсолютной погрешности соизмеримы, то следует их суммировать. (Количество измерений целесообразно увеличить для уменьшения _сл и перехода к случаю 1.)

Принимая во внимание, что вместо _сл можно взять её оценку , то получим:

,

На схеме (рис.1) обобщены методы определения погрешности при прямых измерениях.

Рис.1 Схема определения погрешности прямых измерений

Правила округления погрешности и результата измерения

Рассчитывая значения систематической, случайной и суммарной погрешностей, особенно при использовании электронного калькулятора, получают значение с большим числом знаков. Однако исходные данные для этих расчетов всегда указываются с одной или двумя значащими цифрами. Действительно, класс точности прибора на его шкале указывается не более чем с двумя значащими цифрами, а среднее квадратическое отклонение не имеет смысла записывать с более чем двумя значащими цифрами, так как точность этой оценки при 10 измерениях не выше 30 %. Вследствие этого и в окончательном значении расчетной погрешности должны быть оставлены только первые одна - две значащие цифры. При этом необходимо учитывать следующее. Если полученное число начинается с цифры 1 или 2, то отбрасывание второго знака приводит к очень большой ошибке (до 30– 50 %), это недопустимо. Если же полученное число начинается, например, с цифры 9, то сохранение второго знака, то есть указание погрешности, например, 0,94 вместо 0,9, является дезинформацией, так как исходные данные не обеспечивают такой точности.

В итоге можно сформулировать правила округления рассчитанного значения погрешности и полученного экспериментального результата измерения:

1. Абсолютная погрешность результата измерения указывается двумя значащими цифрами, если первая из них равна 1 или 2, и одной, – если первая есть 3 и более.

2. Среднее значение измеренной величины округляется до того же десятичного разряда, которым оканчивается округленное значение абсолютной погрешности.

3. Относительную погрешность, выраженную в процентах, достаточно записать двумя значащими цифрами.

4. Округление производится лишь в окончательном ответе, а все предварительные вычисления проводятся с одним лишним знаком.

Пример: На вольтметре класса точности 2,5 с пределом измерений 300 В были произведены несколько повторных измерений одного и того же напряжения. При этом оказалось, что все замеры дали одинаковый результат 267,5 В.

Отсутствие различий между знаками говорит о том, что случайная погрешность пренебрежимо мала, поэтому суммарная погрешность совпадает с систематической (см. рис. 1а).

Сначала найдем абсолютную, а затем относительную погрешности. Абсолютная погрешность градуировки прибора равна:

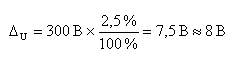
Так как первая значащая цифра абсолютной погрешности больше трех, то это значение должно быть округлено до 8 В. Относительная погрешность:

В значении относительной погрешности должны быть сохранены два значащих разряда: 2,8 %.

Таким образом, в окончательном ответе должно быть сообщено “Измеренное напряжение U=(268+8) В при относительной погрешности _U=2,8 % ”.