3.7 Круговая и параболическая арки
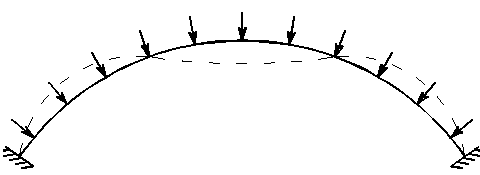
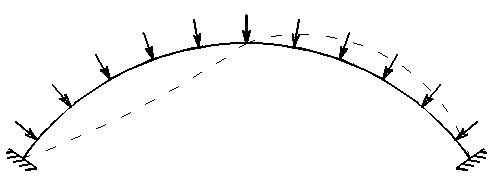
Рассмотрим круговую арку под действием гидростатического давления (рис.3.28).
а |
|
б |
|
Рис.3.28
Незначительными изгибающими моментами, возникающими при обжатии оси арки, можно пренебречь, и тогда при критической нагрузке может произойти потеря устойчивости центрального сжатия, т.е. потеря устойчивости I рода. При этом возможны две формы потери устойчивости — симметричная (рис.3.28,а) и кососимметричная (рис.3.28,б).
Как теоретические расчеты, так и экспериментальные исследования показывают, что в отсутствие промежуточного шарнира кососимметричной форме потери устойчивости соответствует меньшая критическая нагрузка, следовательно, эта форма более опасна, и в первую очередь нужно определять отвечающую ей критическую нагрузку.
Допустим,
что круговая арка радиуса 
с
центральным углом 
и
постоянной жесткостью
упруго
защемлена на опорах. Жесткость упругого
защемления характеризуется коэффициентом 
,
который представляет собой реактивный
момент, возникающий в заделке от
единичного поворота.
Рассмотрим новую равновесную форму арки — кососимметричную (пунктирная линия на рис.3.29).
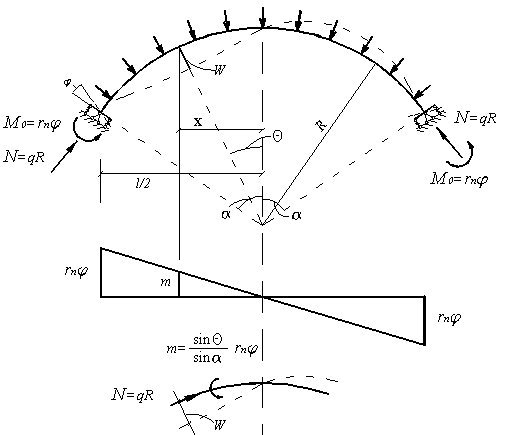
Рис.3.29
Используя статический способ расчета на устойчивость, запишем дифференциальное уравнение изгиба бруса кругового очертания (уравнение Буссинеска):
|
(3.25) |
где 
—
прогиб в произвольном сечении; 
—
угловая координата, отсчитываемая от
оси симметрии; М —
изгибающий момент.
В
деформированном состоянии арки изгибающий
момент М складывается
из момента m,
являющегося следствием упругого
защемления, и момента, создаваемого
продольной силой 
,
причем
,
и тогда
|
(3.26) |
.Подставляя (3.26) в (3.25), получим
,
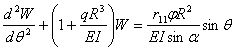или
|
(3.27) |
,где
|
(3.28) |
.Общее решение уравнения (3.27) имеет вид
|
(3.29) |
.Решение (3.29) определяет форму потери устойчивости с точностью до трех параметров А, В, С, для определения которых имеем три граничных условия:
при 
при 
при 
.
Из первого граничного условия следует А = 0; из второго получаем
,
а третье условие с учетом (3.26) принимает вид
.
Дифференцируя (3.29), имеем
,
следовательно
.
Таким образом, для определения А, В, С имеем однородную систему алгебраических уравнений
|
(3.30) |
Система (3.30) имеет ненулевое решение только тогда, когда ее определитель равен нулю:
,
откуда следует уравнение устойчивости
|
(3.31) |
.Определив n, из (3.31) находим критическую нагрузку
|
(3.32) |
.Определим критическую нагрузку на круговую арку, жестко связанную с Г-образными рамами (рис.3.30).
Рис.3.30
Из
уравнения 
находим 
;
.
Для определения нужно рассчитать Г-образную раму методом перемещений. Пропуская промежуточные вычисления, приведем окончательный результат:
.
Подставляя все данные в (3.31), получим уравнение устойчивости
.
Это трансцендентное уравнение легко решается в Mathcad или Matlab:
.
Тогда критическая нагрузка составит
.
Положим, для определенности, что арка имеет прямоугольное сечение 12х6 см, материал — сталь, тогда qкр = 4,591 кН/м.
Решим эту задачу в ANSYS.
1.Задаём геометрические параметры.
Utility Menu > Parameters > Scalar Parameters…
В поле Selection вводим параметры, которые необходимы для расчёта. После ввода каждого параметра нажимаем Accept.
q = 1
a = 20
L = 4
R = 14.5
H1 = 0.12
B1 = 0.06
H2 = 0.095244
B2 = 6 Close.
2.Задаём ключевые точки.
Main Menu>Preprocessor>Modeling > Create > Keypoints > In Active CS
В поле NPT Keypoint number вводим номер точки, в полях X, Y, Z Location in active CS — её координаты.
-
N
1
2
3
4
5
6
X
0
0
-L
a
a
a+L
Y
0
L
L
L
0
L
Z
0
0
0
0
0
0
3.Соединяем точки линиями.
Main Menu>Preprocessor>Modeling>Create>Lines>Lines > Straight Line
Курсором попарно выделяем точки: 1 и 2; 2 и 3; 5 и 4; 4 и 6. ОК.
Точки 2 и 4 соединяем дугой:
Main Menu>Preprocessor>Modeling > Create > Lines > Arcs > By End KPs & Rad
Выбираем точки 2 и 4. ОК. Затем выбираем точку 1, которая определяет плоскость дуги и её выпуклость.
В появившемся окне Arc by End KPs & Radius в поле RAD Radius of the arc вводим величину радиуса: R. OK (рис.3.31).
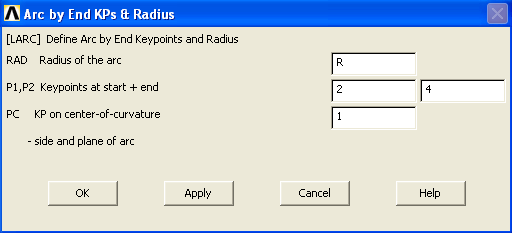
Рис.3.31
4.Задаём тип элемента.
Main Menu > Preprocessor > Element Type > Add / Edit / Delete > Add…
В окне Library оf Element Types выбираем Beam 2D elastic 3. OK. В окне Element Types нажимаем Options… В меню Output at extra intermed pts K9выбираем 9 intermed pts. OK. Close.
5.Задаём реальные константы элемента.
Main Menu > Preprocessor > Real Constants > Add / Edit / Delete > Add…
В окне Element Type for Real Co… нажимаем ОК. В появившемся окне вводим первый набор констант:
AREA: H1*B1: Площадь поперечного сечения
IZZ: (H1*B1**3)/12: момент инерции
HEIGHT: H1 Высота Apply.
Вводим второй набор констант: в поле Real Constant Set No вводим: 2.
AREA: H2*B2
IZZ: (H2*B2**3)/12
HEIGHT: H2 ОК > Close.
6.Задаём свойства материала.
Main Menu > Preprocessor > Material Props > Material Models
В правом поле открывшегося окна двойным нажатием левой кнопки «мыши» выбираем:
Structural > Linear > Elastic > Isotropic
Вводим модуль упругости EX и коэффициент Пуассона PRXY:
EX: 2e11
PRXY: 0.3 OK.
7.Присваиваем атрибуты линиям.
Main Menu > Preprocessor > Meshing > Mesh Attributes > Picked Lines
Выделяем дугу. ОК. В окне Line Attributes в поле REAL Constant set number выбираем – 1. Apply. Выделяем стойки и ригели. ОК. В поле REAL Real constant set number выбираем – 2. ОК.
8.Строим конечно-элементную сетку.
Main Menu > Preprocessor > Meshing > Mesh Tool
Нажимаем кнопку Set рядом с Lines, выделяем дугу. ОК. В поле NDIV No, of element divisions вводим количество разбиений на линии – 30. Apply. Аналогично задаём количество разбиений на линии для стоек и ригелей – 6.
Main Menu > Preprocessor > Meshing > Mesh Tool
В окне Mesh Tool нажимаем Mesh, в окне Mesh Lines – Pick All.
9.Задаём условия закрепления.
Main Menu>Solution>Define Loads>Apply > Structural > Displacement > On Nodes
Выделяем узлы, в которых должна быть жёсткая заделка. ОК. В поле Lab 2 DOFs to be constrained выбираем All DOF. OK.
10.Прикладываем распределённую нагрузку.
Main Menu>Solution>Define Loads>Apply>Structural>Pressure>On Beam
Выделяем элементы, расположенные на дуге. OK. В полях VALI, VALJ вводим величину распределённого давления: q. OK.
Результат препроцессорной подготовки представлен на рис.3.32.
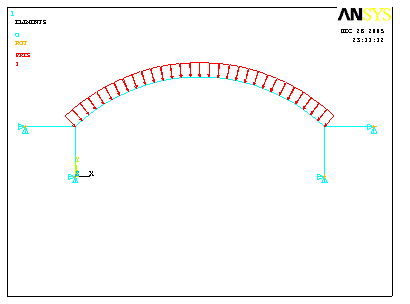
Рис.3.32
Выделяем всю конструкцию:
Utility Menu > Select > Everything
Переходим в командный режим:
FINISH !выход из препроцессора
/SOLU !вход в процессор решения
PSTRES, ON !установить вычисление напряжённого состояния
SOLVE !запуск на решение
FINISH !выход из препроцессора решения
/SOLU !вход в процессор решения
ANTYPE, 1 !анализ на устойчивость в линейной постановке
BUCOPT, SUBSP,5 !определить пять форм потери устойчивости
MXPAND, 5,,, 0
SOLVE !запуск на решение
FINISH
/POST1 !вход в постпроцессор
SET, FIRST !прочитать первый ряд расчётных значений
PLDISP, 1 !вывести деформированную форму графически
SET, NEXT !следующая деформированная форма
PLDISP, 1
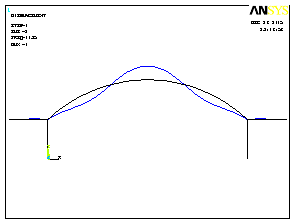
Формы потери устойчивости представлены на рис.3.33.
|
|
1 форма потери устойчивости |
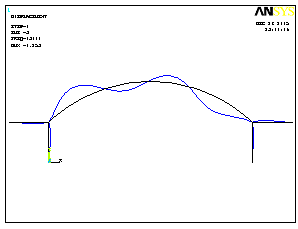
2 форма потери устойчивости |
|
|
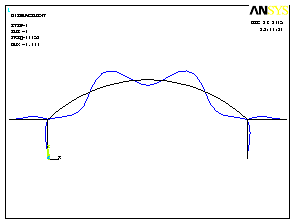
3 форма потери устойчивости |
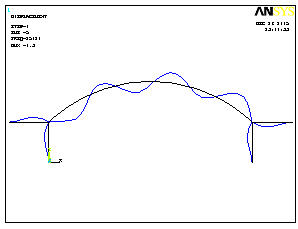
4 форма потери устойчивости |
|
SET TIME/FREQ LOAD STEP SUBSTEP 1 4590.2 1 1 2 7435.2 1 2 3 13048. 1 3 4 18052. 1 4 5 25120. 1 5 |
5 форма потери устойчивости |
Критические нагрузки |
Рис.3.33
Листинг со значениями критических нагрузок (рис.3.33) можно получить следующим образом:
Main Menu > General Postproc > Results Summary
Потеря устойчивости параболической арки, несущей вертикальную равномерно распределенную нагрузку, как и круговой арки, загруженной гидростатическим давлением, характеризуется появлением изгиба, причем, наиболее опасной формой потери устойчивости двухшарнирной и бесшарнирной параболических арок будет кососимметричная.
Дифференциальное уравнение равновесия параболической арки в деформированном состоянии при действии равномерно распределенной нагрузки получено А.Н. Динником. Интегрирование этого уравнения для разных отношений стрелы подъема f к пролету арки l при разных граничных условиях, соответствующих типу арки (бесшарнирная, двухшарнирная и т.п.), дает выражение для критической нагрузки в виде
|
(3.33) |
,где К — коэффициенты устойчивости, значения которых приводятся в справочных таблицах.
Алгоритм расчета параболических арок на устойчивость в ANSYS отличается от приведенного выше порядка расчета круговых арок только на этапе моделирования и в плане приложения вертикальной распределенной нагрузки к арке (см. параграф 2.8).
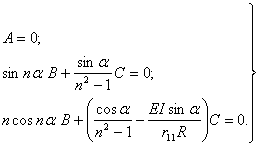