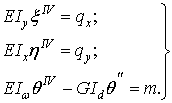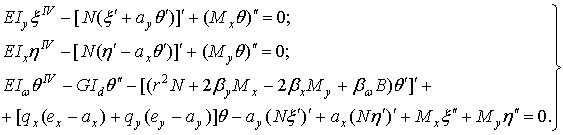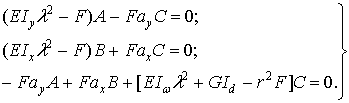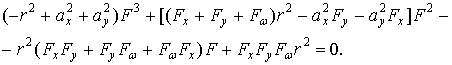3.6 Устойчивость тонкостенных стержней

Дифференциальное уравнение устойчивости 2-го рода

Как установлено В.3. Власовым [7], поперечные сече­ния тонкостенных стержней после деформации, как пра­вило, не остаются плоскими. Эти стержни работают как пространственные тонкостенные системы, испытывающие продольные деформации не только вследствие сжатия или изгиба, но и вследствие закручивания. При этом точ­ки поперечного сечения располагаются на криволиней­ной поверхности; сечение, как говорят, испытывает депланацию. Явление закручивания и связанные с ним дополнительные напряжения играют большую роль в вопросах устойчивости тонкостенных стержней. Будем рассматривать только стержни открытого профиля с недеформируемым контуром поперечного сечения (недеформируемость контура должна быть обеспечена поперечными диафрагмами или ребрами жесткости). Сечения с замкнутым профилем при отсутствии деформации контура могут рассчитываться по обычной теории сплошного бруса с применением гипотезы плоских сечений.

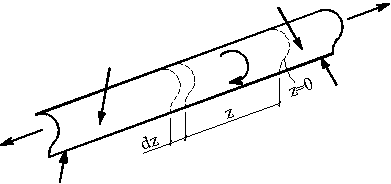
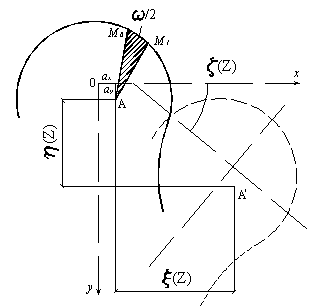
Рассмотрим тонкостенный стержень с недеформируемым профилем, находящийся в равновесии под действием произвольных продольных и поперечных нагрузок (рис.3.21,а).

Поперечное сечение стержня и его перемещение в плоскости ХОУ после деформации показано на рис.3.21,б. Здесь О — центр тяжести сечения; А — центр изгиба;   — соответственно перемещения центра изгиба по направлениям осей х, у и угол поворота всего сечения в плоскости ХОУ(угол за­кручивания); все эти величины являются функциями координаты z сечения вдоль образующей стержня. Кроме того, точки сечения перемещаются в направление оси z; эти перемещения являются функциями координаты s (M₀— М₁) по дуге контура. В рассматриваемом случае потеря устойчивости не связана с появлением новых  форм равновесия, так как и до потери устойчивости, стержень изгибается, закручивается и депланирует;     следовательно, речь идет о потере устойчивости 2-го рода.

 

а
б

Рис.3.21

Поведение тонкостенных стержней в задачах прочности описывается системой трех дифференциальных уравнений, составленных для недеформированного состояния:

(3.16)

где первые два уравнения — это уравнения изгиба стержня, как балки, в направлениях осей х и у, а третье — уравнение стесненного кручения тонкостенного стержня;   и   — интенсивности погонных поперечных нагрузок;  — интенсивность внешнего крутящего момента, опре­деляемого относительно центра изгиба.

Рассмотрим равновесие бесконечно малой по­лоски длиной dz (рис.3.22) тонкостенного стержня в деформированном состоянии.

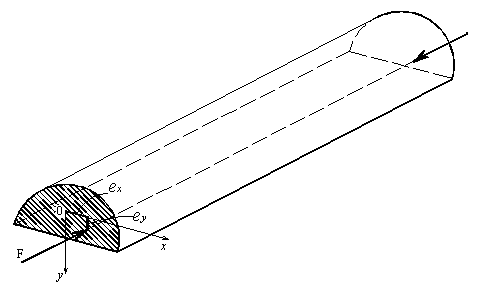
Рис.3.22

Тогда уравнения (3.16) приобретают вид

(3.17)

где

N — продольная сила;

 — изгибающие моменты относительно осей х, у и бимомент соответственно;

 — координаты центра изгиба;

 — координаты точки приложения заданной погонной нагрузки в плоскости поперечного сечения;

 — геометрические характеристики, определяемые по следующим формулам:

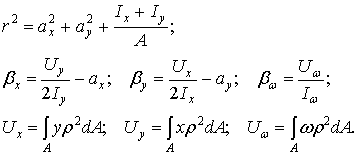
 — полярно-осевые и секториально-полярный моменты инерции;

 — осевые и секториальный моменты инерции;

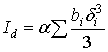 — момент инерции чистого кручения, опре­деляемый для поперечных сечений, со­стоящих из отдельных прямоугольников или криволинейных полос со сторонами  ( 1,3 — для  двутавров;  1,12 — для   швеллеров;  1,0 — для уголков и т. д.).

Уравнения (3.17) являются наиболее общими уравне­ниями устойчивости тонкостенного стержня.

Потеря устойчивости 1-го рода

Если поперечная нагрузка и реакции тонкостенного стержня проходят через линию центров изгиба, то до потери устойчивости стержень не испытывает кручения, депланация отсутствует, она проявляется только в результате потери устойчивости. Таким образом, потеря устойчивости будет характеризоваться появлением качественно нового деформированного состояния, новой формы равновесия, и уравнения (3.17) при бимоменте   будут описывать явление потери устойчивости 1 -го рода.

Для такого внецентренно сжатого стержня (рис.3.20) имеем:

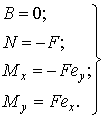
(при определении знаков М_х и М_у поступаем так: при взгляде от положительного направления оси к центру момент по часовой стрелке считается положительным). Уравнения устойчивости (3.17) при внецентренном сжатии принимают вид

(3.18)

Рассмотрим случай центрального сжатия, когда сила приложена в центре тяжести сечения, но центр тяжести не совпадает с центром изгиба; в этом случае

,

и уравнения устойчивости будут такими:

(3.19)

Дифференциальными уравнениями (3.19) и условиями закрепления стержня по концам определяются все фор­мы потери устойчивости невесомого стержня при его центральном сжатии. В каждое из уравнений (3.19) вхо­дят одновременно поступательные перемещения   и углы закручивания  ; это свидетельствует о том, что если центр изгиба не совпадает с центром тяжести ( ), то эйлеровская изгибная форма потери устойчивости при центральном сжатии становится невозможной. В част­ном случае, когда центр изгиба совпадает с центром тя­жести (например, в сечении с двумя осями симметрии) а_х = а_у = 0, и уравнения (3.19) распадаются на три отдель­ных уравнения

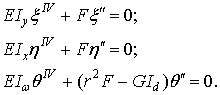
Решения первых двух уравнений дают две эйлеровские критические силы, соответствующие изгибу относи­тельно осей х и у, решение третьего уравнения дает кри­тическую силу  , соответствующую чисто крутильной форме потери устойчивости.

Уравнения (3.19) характеризуют наличие одновременно изгиба и кручения при потере устойчивости, или, как говорят, изгибно-крутильную форму потери устойчи­вости.

Рассмотрим случай, когда концы стержня закреплены от перемещений в плоскости поперечного сечения и свободны от нормальных напряжений, вызываемых изгибом и кручением, т. е.

  при   и при     

Этим граничным  условиям   и  дифференциальным уравнениям (3.19) будет удовлетворять решение в виде

(3.20)

где А, В, С — некоторые постоянные коэффициенты; i — любое целое положительное число (i = 1,2,3...).

Подставляя (3.20) в уравнения (3.19) и вводя обозначение

,

(3.21)

получаем после сокращения на общий множитель   систему однородных линейных ал­гебраических уравнений

(3.22)

Ненулевое решение для неизвестных  А, В, С возможно только в случае равенства нулю определителя, составленного из коэффициентов при этих неизвестных.

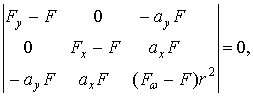
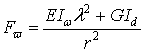где   — эйлеровские критические силы;   — критическая сила для чисто крутильной формы  потери устойчивости.

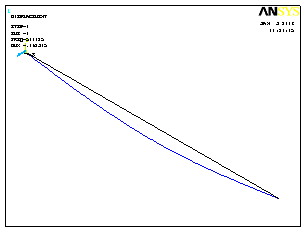
Раскрывая определитель, получим уравнение устойчивости, из которого определяется критическое значение нагрузки:  

(3.23)

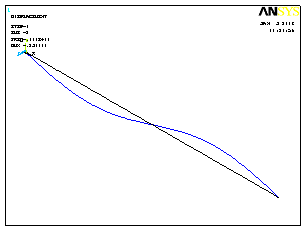
или, располагая по степеням F,

(3.24)

Уравнение (3.24) — кубическое относительно силы F, имеет три корня F₁, F₂, F₃, соответствующие трем степе­ням свободы поперечного сечения с недеформируемым контуром в своей плоскости. Каждый из этих корней будет зависеть от числа полуволн n (n = 1, 2, 3, ...,  ), т. е. будет иметь бесконечное множество значений в соответствии с бесконечным числом степеней свободы упругой оси стержня.

Пусть F₁ < F₂ < F₃, а из эйлеровских критических сил минимальной будет F_х:

< < .

Представим уравнение (3.24) в виде   и иссле­дуем характер функции  , произвольно изображенной на рис.3.23.

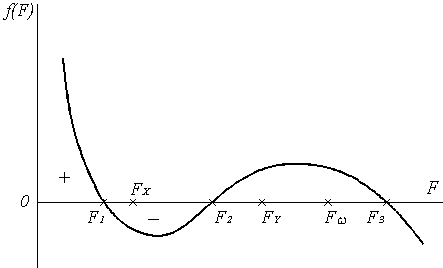
Рис.3.23

Из уравнения (3.24) видно, что при малых зна­чениях F знак   должен совпадать со знаком свобод­ного члена, т. е.   > 0 при F < F₁. Из (3.24) находим, что

        при  < 0, т.е. значение   располагается между   и  ;

        при   > 0;

        при   > 0, т.е. значения   и   располагаются между корнями  ,  .

При больших значениях F знак   будет совпадать со знаком старшего члена:

< 0, т.е.  < 0.

Основной, практически очень важный вывод, который следует из этих рассуждений, заключается в следующем: для несимметричного тонкостенного стержня, в котором центр изгиба не совпадает с центром тяжести, критичес­кая сила, соответствующая изгибно-крутильной форме потери устойчивости, всегда меньше минимальной эйлеровской критической силы.

В частном случае, если центр изгиба совпадает с цент­ром тяжести сечения, имеем а_х = а_у = 0, и уравнение (3.24) принимает вид

откуда получаем три решения:

т. е. в этом случае имеем или чисто изгибную, или чисто крутильную форму потери устойчивости, что уже было показано выше непосредственно на дифференциальных уравнениях.

При внецентренном сжатии чисто изгибные и чисто крутильные формы потери устойчивости имеют место, ес­ли сила приложена в центре изгиба. В этом случае   и уравнения (3.19) тоже распадаются на три самостоятельных уравнения

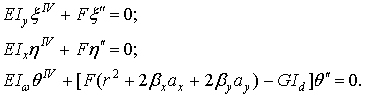
Первые два уравнения определяют изгибные формы потери устойчивости и дают эйлеровские критические си­лы  ; третье уравнение определяет крутильную форму потери устойчивости, при которой по­перечные сечения стержня поворачиваются вокруг цент­ра изгиба; при этом величина критической силы оп­ределится по формуле

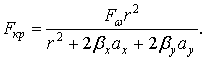
Расчетной будет минимальная из трех критических сил.

В [22] определены эйлеровские критические си­лы и критическая сила свободного кручения для шарнирно опертого двумя концами стержня длиной l = 9 м, находящегося под действием постоянной продольной, центрально приложенной силы F. Поперечное сечение стержня — сварное, из стальных листов (рис.3.24).

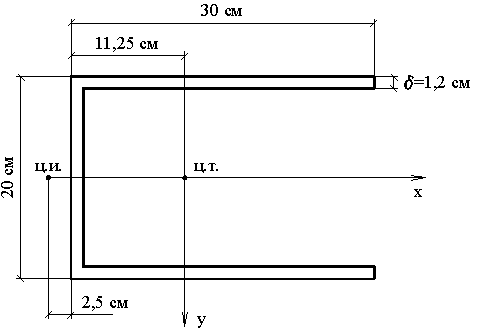
Рис.3.24

При   получены эйлеровские критические силы  , критическая сила свободного кручения   и критические силы, соответствующие изгибно-крутильной форме потери устойчивости 

Решим эту задачу в программе ANSYS.

1. Задаем геометрические параметры балки.

Utility Menu > Parameters > Scalar Parameters…

В поле Selection вводим параметры, которые будут использоваться в расчете. После ввода каждой константы нажимаем Accept.

H = 0.3 !высота поперечного сечения

B = 0.2 !ширина поперечного сечения

S = 0.012 !толщина стенок

L = 9 !длина балки

F = 1 !единичная сосредоточенная сила

2. Задаем конечный элемент и его опции.

Main Menu > Preprocessor > Element Type > Add/Edit/Delete > Add…

В окне Library of Element Types выбираем BEAM 3 node 189. OK. В окне Element Type нажимаем кнопку Options… В появившемся окне BEAM189 element type options выбираем:

Warping degree of freedom K1 — Restrained

Cross section scaling is K2 — Rigid (classic)

Shear stress output K4 — Include Both         OK, Close.

3. Выбираем поперечное сечение.

Main Menu > Preprocessor > Sections > Beam > Common Sections

В окне Beam Tool в поле Name вводим имя сечения — channel bar. В выпадающем меню Sub Type выбираем схему с изображением швеллера, в меню Offset To — Centroid.

Ниже задаем геометрические параметры сечения:

W1: H        t1: S

W2: H        t2: S

W3: B        t3: S

Бегунок (Coarse-Fine), регулирующий плотность сетки, выставляем на единицу. Кнопка Meshview прорисовывает на мониторе сечение с сеткой и вычисленные программой геометрические характеристики (рис.3.25).

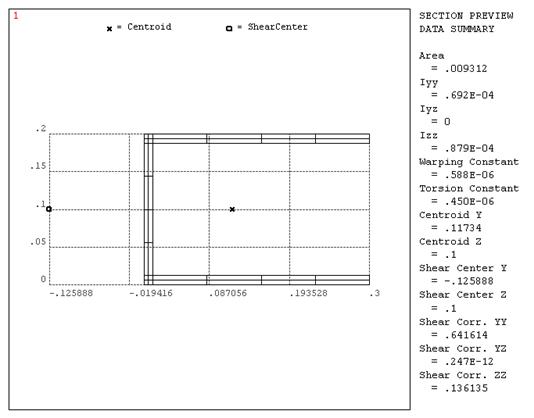
Рис.3.25

4. Задаем свойства материала.

Main Menu > Preprocessor > Material Props > Material Models

В появившемся окне выбираем:

Structural > Linear > Elastic > Isotropic

Вводим модуль упругости EХ и коэффициент Пуассона PRXY:

EX: 2e11

PRXY: 0.3  OK.

5. Построение модели.

5.1. Задаем ключевые точки.

Main Menu>Preprocessor > Modeling > Create > Keypoints > In Active CS

В поле NPT Keypoint  number вводим номер точки, в полях x, y, z Location in active CS — ее координаты:

точка 1 (0; 0; 0), точка 2 (L; 0; 0), точка 3 (L/2; B; 0).

5.2. Соединяем точки линиями.

Main Menu>Preprocessor>Modeling>Create>Lines > Lines > Straight Line

Выделяем точки 1 и 2. ОК.

6. Присваиваем атрибуты линии.

Main Menu > Preprocessor > Meshing > Mesh Attributes > Picked Lines

В окне выбора нажимаем Pick All. В диалоговом окне Line Attributes в строке Pick Orientation Keypoint(s) ставим переключатель из No в Yes. ОК. Выделяем точку 3. ОК. Точка 3 является точкой ориентации сечения.

7. Задаем количество разбиений на линии.

Main Menu>Preprocessor > Meshing > Size Cntrls > ManualSize > Lines > Picked Lines

В появившемся окне нажимаем Pick All. В поле NDIV No. of element divisions задаем количество разбиений на линии — 36. ОК.

8. Строим сетку.

Main Menu > Preprocessor > Meshing > Mesh Tool

В окне Mesh Tool нажимаем Mesh, в Mesh Lines — Pick All.

Пронумеруем точки:

Utility Menu > PlotCtrls > Numbering…

В строке KP Keypoints numbers ставим переключатель из Off в On. ОК.

Прорисуем линии:

Utility Menu > Plot  > Lines

9. Задаем условия закрепления.

Main Menu > Solution > Define Loads > Apply>Structural>Displacement> On Keypoints

Выделяем точку 1. ОК. В окне Apply U, ROT on KPs выбираем UX, UY, UZ. Apply. Затем выделяем точку 2. ОК. В окне Apply U, ROT on KPsвыбираем UY, UZ. ОК.

10. Прикладываем сосредоточенную нагрузку.

Main Menu>Solution > Define Loads > Apply>Structural>Force/Moment > On Keypoints

Выделяем точку 2. ОК. В диалоговом окне Apply F/M on KPs в выпадающем меню Lab Direction of force/mom выбираем FX, в поле VALUEForce/moment value вводим величину нагрузки: -F. ОК.

11. Переходим от схематического изображения модели к реальному.

Utility Menu > PlotCtrls > Style > Size and Shape…

В строке [/ESHAPE] Display of element ставим переключатель из Off в On. ОК.

Прорисуем элементы:

Utility Menu > Plot > Elements

Просмотрим модель в изометрии (рис.3.26).

Выделяем всю конструкцию:

Utility Menu > Select > Everything

12. Переходим в командный режим ANSYS Command Prompt.

FINISH

/SOLU

PSTRES, ON !Установить вычисление напряженного состояния

SOLVE

FINISH

/SOLU

ANTYPE, 1 !Анализ на устойчивость в линейной постановке

BUCOPT, SUBSP, 5 !Определить пять форм потери устойчивости

MXPAND, 5,,, 0

SOLVE !Запуск на решение

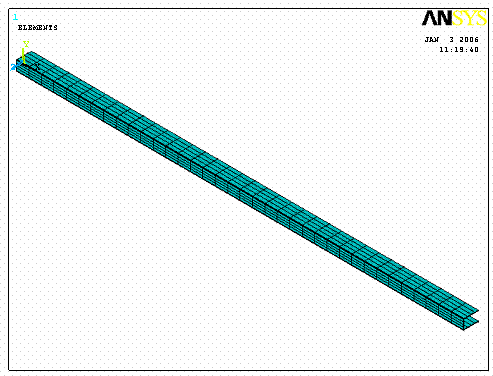
Рис.3.26

На этапе просмотра форм потери устойчивости более наглядным будет схематическое изображение стержня в виде линии.

FINISH ! Выход из препроцессора

/POST1 ! Вход в постпроцессор

SET,FIRST ! Просчитать первый ряд расчетных значений

PLDISP,1 ! Вывести деформированную форму графически

SET,NEXT ! Следующая деформированная форма

PLDISP,1

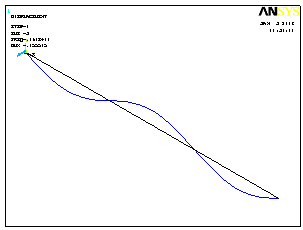
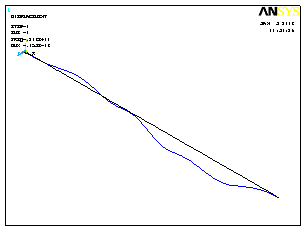
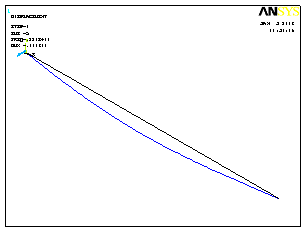
Формы потери устойчивости показаны на рис.3.27. Листинг со значениями критических сил (рис.3.27) выводится с помощью меню:

Main Menu > General Postproc > Results Summary

1 форма	2 форма
3 форма	4 форма
	SET   TIME/FREQ    LOAD  STEP   SUBSTEP         1    0.51072E+06         1                 1                2    0.10965E+07         1                 2                3    0.19812E+07         1                 3                4    0.21562E+07         1                 4                5    0.22384E+07         1                 5
5 форма	Листинг

Рис.3.27

Некоторое расхождение с результатами аналитического расчета объясняется тем, что в программе ANSYS геометрические характеристики сечения вычислены точно, а при аналитическом расчете — приближенно.