- •Глава 3. Расчет конструкций на устойчивость
- •3.1 Основные теоретические положения расчета на устойчивость
- •3.2 Подходы к расчетам на устойчивость в программе ansys
- •3.3 Критические силы и формы потери устойчивости сжатых стержней
- •3.4 Устойчивость неразрезных балок
- •3.5 Устойчивость плоских рам
- •3.6 Устойчивость тонкостенных стержней
- •3.7 Круговая и параболическая арки
- •3.8 Устойчивость прямоугольных пластин
- •3.9 Устойчивость оболочек
- •Вводим модуль упругости и коэффициент Пуассона:
- •3.10 Пластины с ребрами жесткости
- •В полях ex и prxy вводим модуль Юнга и коэффициент Пуассона:
- •3.11 Цилиндрические панели
- •Вводим модуль упругости eх и коэффициент Пуассона prxy:
3.3 Критические силы и формы потери устойчивости сжатых стержней
Известно [25], что впервые задачу об устойчивости сжатого стержня решил Л. Эйлер. Он определил величину критической силы для стержня с шарнирным опиранием по концам (рис.3.6).
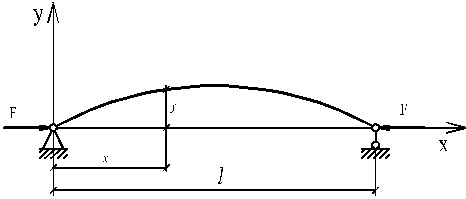
Рис.3.6
|
(3.5) |
При ![]() формы
равновесия, определяемые формулой
(3.5), неустойчивы; для их существования
требуются дополнительные условия,
поэтому чаще всего формулу Эйлера
записывают в виде
формы
равновесия, определяемые формулой
(3.5), неустойчивы; для их существования
требуются дополнительные условия,
поэтому чаще всего формулу Эйлера
записывают в виде
|
(3.6) |
Значению критической силы (3.6) изгиб стержня по синусоиде с одной полуволной
![]()
При условиях опирания стержня, отличных от шарнирного, (3.6) принимает вид
|
(3.7) |
где ![]() -
коэффициент приведения длины, зависящий
от условий опирания концов стержня.
Например, при одном свободном конце и
другом защемленном
-
коэффициент приведения длины, зависящий
от условий опирания концов стержня.
Например, при одном свободном конце и
другом защемленном ![]() ;
при одном шарнирном и другом защемленном
;
при одном шарнирном и другом защемленном ![]() ;
при обоих защемленных концах
;
при обоих защемленных концах ![]()
В практических расчетах часто удобнее использовать не критическую силу, а критическое напряжение, которое с учетом (3.7) можно определить по формуле
|
(3.8) |
где
величина 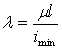 называется
гибкостью стержня (
называется
гибкостью стержня (![]() — минимальный
радиус инерции поперечного сечения).
— минимальный
радиус инерции поперечного сечения).
Формула
Эйлера получена при помощи интегрирования
дифференциального уравнения изогнутой
оси стержня; при этом предполагается,
что критические напряжения в момент
потери устойчивости не превышают предел
пропорциональности материала ![]() .
А это означает, что пределы применимости
формулы Эйлера также ограничены пределом
пропорциональности или, если в качестве
критерия использовать гибкость стержня
.
А это означает, что пределы применимости
формулы Эйлера также ограничены пределом
пропорциональности или, если в качестве
критерия использовать гибкость стержня ![]() ,
величиной
,
величиной
|
(3.9) |
Очевидно,
что нижний предел величины
будет
различным при подстановке в (3.9) значений
модуля упругости и предела пропорциональности
разных материалов (например, для стали
Ст3 такая подстановка означает, что
формула Эйлера применима при ![]() ).
).
При напряжениях, превышающих предел пропорциональности, решение задачи об устойчивости сжатого стержня распадается на два варианта. Так называемые ”короткие стержни” (с малым отношением длины к габаритному размеру сечения) на устойчивость не рассчитываются, так как они перестают работать от потери прочности раньше, чем от потери устойчивости.
Что
же касается стержней со ”средней”
гибкостью (для стали Ст3 это
интервал ![]() ),
то для них величина критической силы
определяется по эмпирической формуле
Ф. Ясинского
),
то для них величина критической силы
определяется по эмпирической формуле
Ф. Ясинского
|
(3.10) |
где А –
площадь поперечного сечения; ![]() и
и ![]() –
коэффициенты, имеющие размерность
напряжений и зависящие от вида материала
(например, для стали Ст3 принимают a
= 310 МПа, b =1,14 МПа).
–
коэффициенты, имеющие размерность
напряжений и зависящие от вида материала
(например, для стали Ст3 принимают a
= 310 МПа, b =1,14 МПа).
С
учетом изложенного для каждого материала
можно построить полный график зависимости
критических напряжений от гибкости. Для
стали Ст3 (![]() )
такой график представлен на рис.3.7.
)
такой график представлен на рис.3.7.

Рис.3.7
График состоит из трех частей: гипербола Эйлера – участок ВС, наклонная прямая, соответствующая формуле Ясинского, – участок СД и горизонтальная или, точнее, слабо наклонная прямая ДК, отвечающая ”коротким” стержням.
В качестве примера расчета на устойчивость рассмотрим жестко защемленный стальной стержень ( ) прямоугольного поперечного сечения (рис.3.8).

Рис.3.8
При
указанных условиях гибкость стержня ![]() ,
и критическая сила, вычисленная по
формуле Эйлера, составит
,
и критическая сила, вычисленная по
формуле Эйлера, составит ![]() .
.
Решим эту же задачу в ANSYS, поставив целью определение пяти критических сил и соответствующих им форм потери устойчивости.
1. Задаём тип элемента и его опции.
Main Menu > Preprocessor > Element Type > Add/Edit/Delete > Add…
Из библиотеки конечных элементов программы ANSYS выбираем балочный элемент BEAM3, который предназначен для решения двумерных задач. Данный элемент работает на растяжение-сжатие и изгиб.
В появившемся окне Library of Element Types в левом поле выбираем Beam. В правом поле — 2D elastic 3. OK. В окне Element Types нажимаем кнопку Options… В строке Output at extra intermed pts K9 выбираем 9 intermed pts. OK, Close.
2. Задаём реальные константы элемента.
Main Menu>Preprocessor>Real Constants>Add/Edit/Delete>Add…>OK
В диалоговом окне необходимо задать площадь поперечного сечения AREA, момент инерции IZZ, высоту сечения HEIGHT:
AREA – 0.04 * 0.06
IZZ – (0.06 * 0.04 * * 3) / 12
HEIGHT – 0.06. OK, Close.
3. Задаём свойства материала.
Main Menu > Preprocessor > Material Props > Material Models
В правом поле появившегося окна, двойным нажатием левой кнопки «мыши» выбираем:
Structural > Linear > Elastic > Isotropic
Вводим модуль упругости EX и коэффициент Пуассона PRXY:
EX – 2e11
PRXY – 0.3 OK.
4. Задаём узлы.
Main Menu > Preprocessor > Modeling > Create > Nodes > In Active CS
В строке NODE Node number вводим номер узла, а в строках X, Y, Z Location in active CS — его координаты:
узел 1 — (0, 0, 0); узел 20 — (0, 1, 0)
Задаём промежуточные узлы:
Main Menu>Preprocessor>Modeling > Create > Nodes > Fill between Nds
При появлении окна Fill between Nds выделяем узлы 1 и 20. OK. В строке NFILL Number of nodes to fill стоит цифра 18. Это означает, что между узлами 1 и 20 будет построено восемнадцать узлов. OK.
5. Определяем элемент BEAM3 на каждом участке.
Main Menu>Preprocessor>Modeling>Create>Elements>Auto Numbered> Thru Nodes
Попарно, в порядке возрастания, выделяем узлы. После выделения каждой пары нажимаем Apply, после последней – OK.
6. Задаём условия закрепления.
Main Menu>Solution>Define Loads>Apply > Structural > Displacement > On Nodes
Выделяем узел 1. OK. В окне Apply U, ROT on Nodes выбираем All DOF. OK.
7. Прикладываем единичную нагрузку.
Main Menu>Solution>Define Loads>Apply>Structural>Force/Moment> On Nodes
Выделяем узел 20. OK. В появившемся окне Apply F/M on Nodes в поле Lab Direction of force/mom выбираем FY, в поле VALUE force/moment valueвводим: - 1. OK (рис.3.9).
Рис.3.9
8. Выделяем всю конструкцию.
Utility Menu > Select > Everything
Переходим в командный режим:
FINISH !выход из препроцессора
/SOLU !вход в процессор решения
PSTRES, ON !установить вычисление напряжённого состояния
SOLVE !запуск на решение
FINISH !выход из препроцессора решения
/SOLU !вход в процессор решения
ANTYPE, 1 !анализ на устойчивость в линейной постановке
BUCOPT, SUBSP,5 !определить пять форм потери устойчивости
MXPAND, 5,,, 0
SOLVE !запуск на решение
FINISH
/POST1 !вход в постпроцессор
SET, FIRST !прочитать первый ряд расчётных значений
PLDISP, 1 !вывести деформированную форму графически
SET, NEXT !следующая деформированная форма
PLDISP, 1
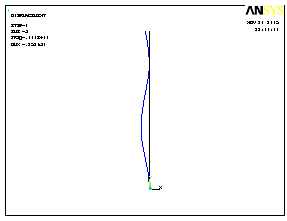
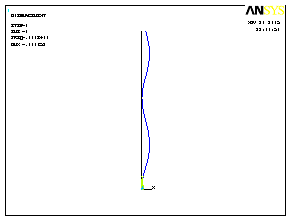
Формы потери устойчивости показаны на рис.3.10.
|
|
1 форма |
2 форма |
|
|
3 форма |
4 форма |
|
|
5 форма |
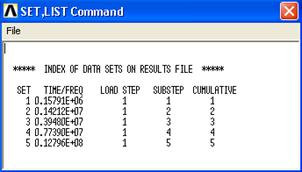
Листинг |
Рис.3.10
Листинг со значением критических сил можно получить так (рис.3.10):
Main Menu > General Postproc > Results Summary