IV. Формування вмінь.

Завдання високого рiвня розбираються бiля дошки, а достатнього коментуються учнями з мiсця.

1. Знайдiть значення виразу · .

Розв`язання

= = = = 3.

Вiдповiдь: 3.

2. Звiльнiться вiд iррацiональностi в знаменнику дробу .

Розв`язання

= = .

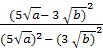Вiдповiдь: .

3. Винесiть множник з-пiд знака радикала .

Розв`язання

= = ² .

Вiдповiдь: ² .

4. Внесiть множник пiд знак радикала ( +b) .

Розв`язання

= .

Вiдповiдь:

5. Спростiть вираз .

Розв`язання

= .

Вiдповiдь: .

6. Порiвняйте i .

Розв`язання

= = , = = .

. Отже, <

Вiдповiдь: <

7. Обчислiть · .

Розв`язання

Вiдповiдь: 1.

8. Знайдiть значення виразу , якщо x = 3,5.

Розв`язання

= .

Оскiльки х = 3,5, то 4-х>0, тодi |4-x| = 4-x.

= = -1.

Вiдповiдь: -1.

9. Спростiть вираз .

Розв`язання

= ( = 2² = 4.

Вiдповiдь: 4.

10.Знайдiть значення виразу , якщо а=-10, b=2.

Розв`язання

= : = · = .

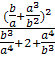Якщо = -10, b = 2, то = = 50.

Вiдповiдь: 50.

V. Пiдведення пiдсумкiв уроку.

Учитель звертає увагу учнiв на головне на даному уроцi i вiдповiдає на запитання учнiв.

VI. Домашнє завдання.

1. Знайдiть значення виразу:

а) ; б) + 4( )⁶ – 3 ;

в) (2 ) ^-1,5; г) · 49^1,25.

2. Звiльнiться вiд iррацiональностi в знаменнику дробу:

а) ; б) .

3. При яких значеннях змiнної х не має змiсту вираз:

а) ; б) ?

4. Знайдiть область допустимих значень виразу:

а) ; б) (х² – 4)⁰.

Довідковий матеріал

1. Означення

Означення	Приклади
Корiнь n-го степеня з числа – це таке число, n-й степiнь якого дорiвнює числу (n є N). – корiнь, n – показник, – пiдкореневий вираз.	= 5, 54 = 625; = -7, (-7)3 = -343.
Арифметичним коренем n-го степеня з невiд`ємного числа називається таке число , n-й степiнь якого дорiвнює .	= 2 – арифметичний корiнь.
Показники коренiв вигляду n=2k+1 використовують для позначення будь-яких коренiв; показники вигляду n=2k – тiльки для позначення арифметичних коренiв. n є N, але n ≠ 1.	= -3; = 8.
Степенем числа >0 з рацiональним показником r = , де m – цiле, а n>1 – натуральне число, називають число , тобто = .	= = 9 ; = .

2. Властивості кореня

Властивостi коренiв n-го степеня	Приклади
(n є N, n≠1): 1. = 0 2. = 1 3. , ≥0, b≥0 4. . ≥0, b≥0 5. = , ≥0, b>0 6. = , ≥0, b>0 7. ( )k = , >0, kєZ (якщо kєN, то рiвнiсть справджується й тоді, коли =0) 8. = = , 0, m є N, k є N, m≠1, k≠1 9. = , m є N, q є N, m≠1.	= = 2 = · = 3·2 = 6 = = (2 = 23 = 8 · 0,3 = 2,4 = =