Тема 5. Аксіоматична семантика

Завдання 5.1. Довести часткову коректність програми DIV(a,b) (див. завдання 1.2) за допомогою логіки Хоара (в аксіоматичній семантиці).

Розв’язок.

Введемо позначення:

DIV(a,b) = rez:=0; k:=0; if a=0 then skip else if a<0 then skip else while k<=a-b do begin rez:=rez+1;k:=k+b end; ost:=a-k	S1 = rez:=0; k:=0; S2 = if a=0 then skip else if a<0 then skip else while k<=a-b do begin rez:=rez+1;k:=k+b end; ost:=a-k
IF1 = if a=0 then skip else if a<0 then skip else while k<=a-b do begin rez:=rez+1;k:=k+b end	IF2 = if a<0 then skip else while k<=a-b do begin rez:=rez+1;k:=k+b end
WH = while k<=a-b do begin rez:=rez+1;k:=k+b end	S3 = rez:=rez+1;k:=k+b

Тоді маємо наступне виведення в логіці Хоара:

(*) =

(**) =

(***) =

де предикати мають такий вигляд:

Інваріант цієї задачі для циклу while: P={rez=k/b}.

Розглянемо предикат qf: з нього випливає, що . Далі, і при цьому . Звідси випливає, що , тобто скільки разів b повністю укладається в a, або ж ціла частина від ділення, тоді – залишок від ділення a на b за означенням.

Таким чином, з істинності (предиката q0) як передумови випливає істинність (отриману з предиката qf еквівалентними перетвореннями) як післяумови, і це доводить часткову коректність програми.

Завдання 5.2.

1) Побудувати програму обчислення n! через операцію «+».

2) Довести часткову коректність побудованої програми за допомогою логіки Хоара (в аксіоматичній семантиці).

Розв’язок.

1) Програма обчислення n! через операцію додавання:

Prog(n) =

begin

res := 1;

i : = 1;

w hile i <= n do

begin

j := 1;

k

F3 або WH(…)₁

F2

:= res;

while j < i do

b

F4

egin

k

S2

WH(…)₂

F5

:= k + res;

j := j+1

end;

r

F6

es := k;

i := i + 1

end

end

На тексті програми введено позначення (скорочення), які ми будемо використовувати далі.

2) Доведення часткової коректності.

Деякі предикати, які зустрінуться в доведенні:

Необхідно показати, що в результаті обчислень за програмою ми отримаємо , що еквівалентно qf.

Решту предикатів ми будемо обчислювати в ході виведення (доведення) в логіці Хоара:

(1)

(2)

(3)

(4)

(5)

(6)

Таким чином, з істинності (предиката T) як передумови випливає істинність (предиката qf) як післяумови, що доводить часткову коректність програми.

Завдання 5.3. Довести часткову коректність програми Sum_fac(n) обчислення суми факторіалів до вхідного n≥0 (включно) через множення і додавання (див. завдання 4.3) за допомогою логіки Хоара (в аксіоматичній семантиці).

Розв’язок.

Введемо позначення:

Sum_fac(n) = i:=0; fac:=1; res:=1; while i ≠ n begin i:=i+1; fac:= fac*i; res:=res+fac end

W = while i ≠ n begin i:=i+1; fac:= fac*i; res:=res+fac; end

Позначення предикатів:

P =

P₀ =

P₀₁ =

P₀₂ =

T =

T₀ =

T₁ =

B =

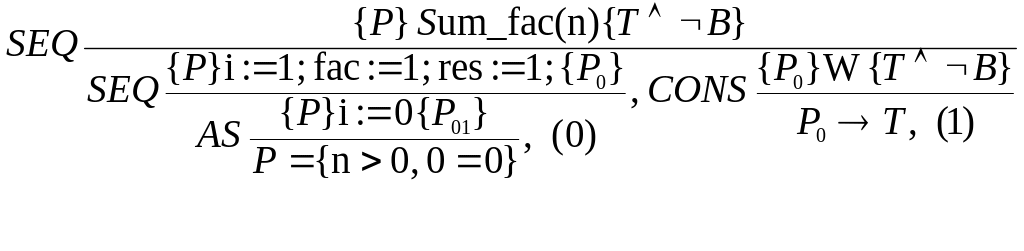
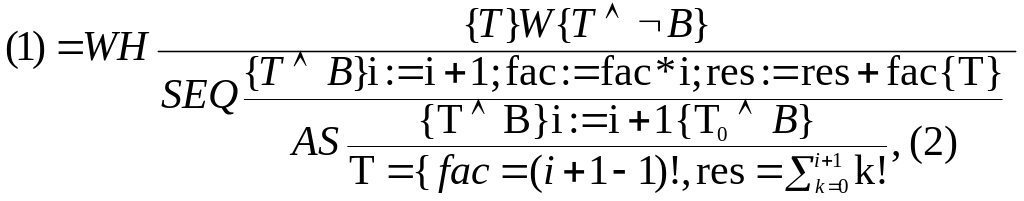
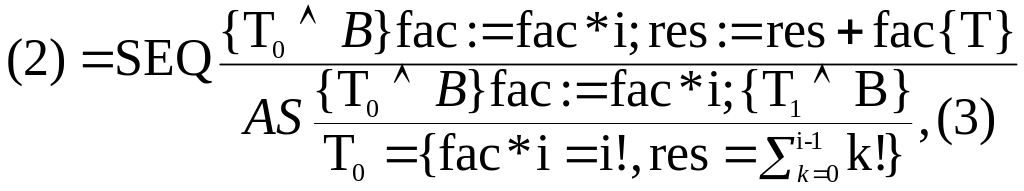
Таким чином, з істинності (предиката P) як передумови випливає істинність (як предиката , тобто та {i = n}) як післяумови, що і доводить часткову коректність програми.