Пример 3.7
Найти координаты
точки
,
симметричной точке
относительно прямой, проходящей через
точки
и
.
Решение:
Составим уравнение
прямой
.
Для этого воспользуемся уравнением
прямой, проходящей через две точки
и
:
.
Для прямой имеем: , .
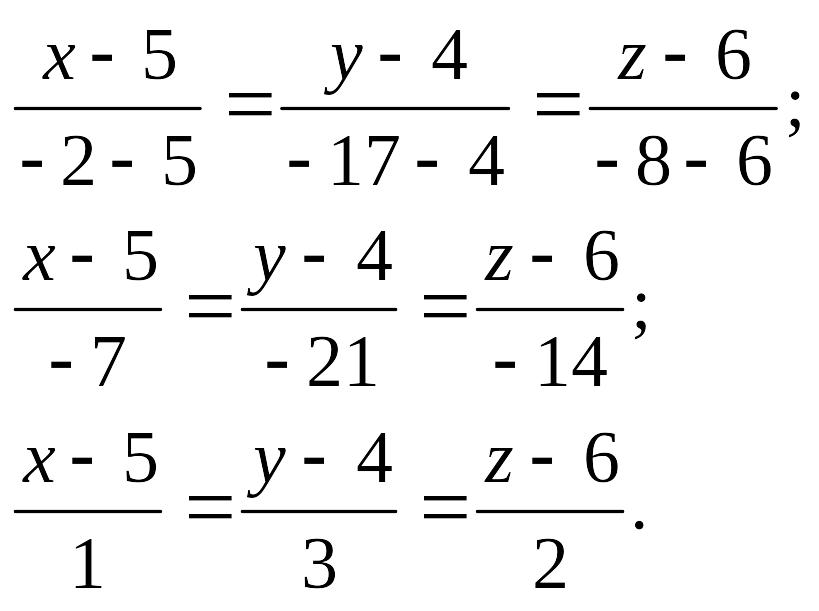
Найдем координаты
точки
,
симметричной точке
относительно прямой
.
Через точку
проводим плоскость
перпендикулярно к вектору
.
Получим:
Найдем точку пересечения плоскости и прямой . Уравнение прямой представляем в параметрическом виде:
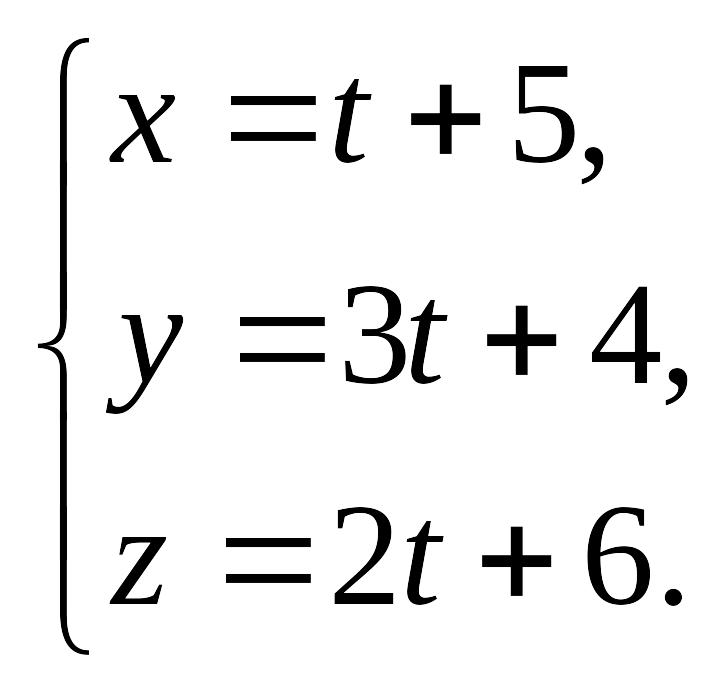
Учитывая, что точка
,
пересечения прямой
и плоскости
,
лежит и на прямой и на плоскости, получим:
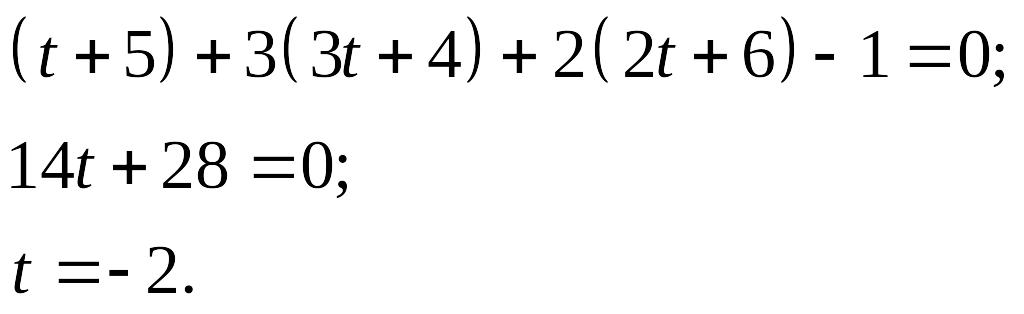
Значит
.
Точка
- середина отрезка
.
Координаты точки
найдем из соотношений:
.
Получим:
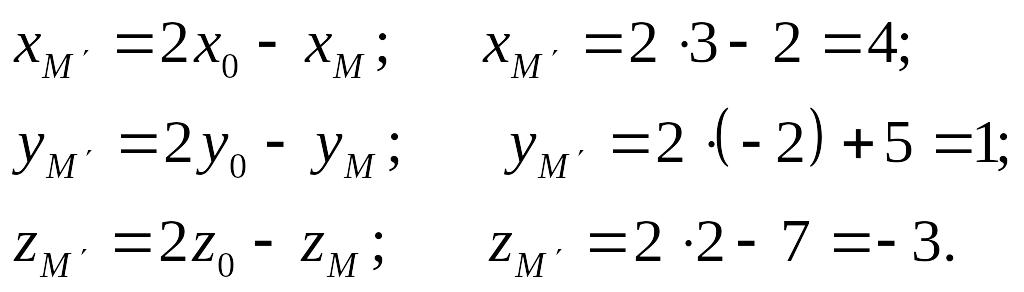
Точка
симметрична точке
относительно прямой
.
Ответ: .
Пример 3.8
Найти точку
,
симметричную точке
относительно плоскости
:
.
Решение:
Прежде всего,
найдем проекцию
точки
на плоскость
.
Для этого составим уравнение прямой
,
перпендикулярной к данной плоскости.
Нормальный вектор плоскости
будет направляющим вектором перпендикуляра
.
Используем каноническое уравнение
прямой, проходящей через точку
с направляющим вектором
:
.
Имеем, прямая
проходит через точку
и
:
.
Найдем точку пересечения прямой и плоскости . Для этого приведем уравнение прямой к параметрическому виду:
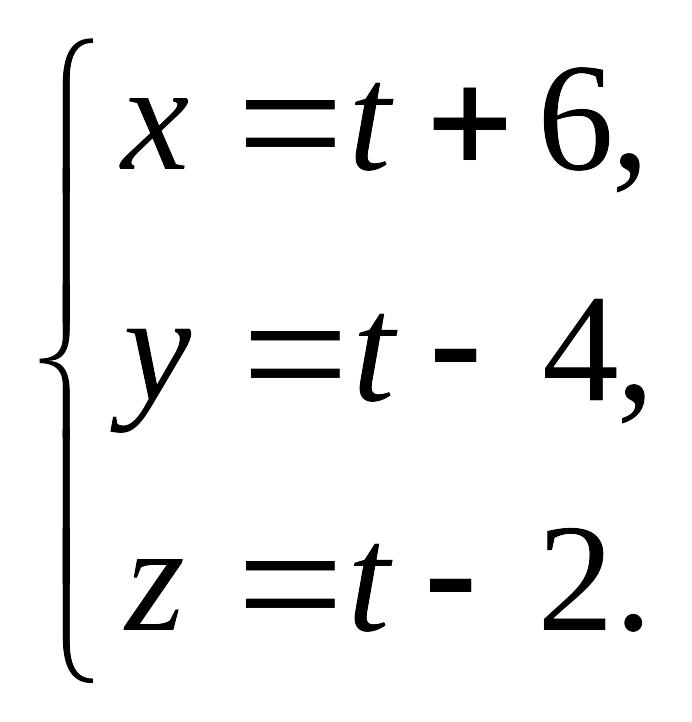
Подставляя значения
из этих уравнений в уравнение плоскости
,
найдем:
Получили
- значение параметра, отвечающее точке
как точке пересечения прямой
с плоскостью
.
Следовательно,
,
то есть
.
Учитывая, что точка середина отрезка , найдем ее координаты:
.
.
.
Таким образом,
точка
- симметричная точке
относительно плоскости
:
.
Ответ: .
Задания для самостоятельного решения.
Задание 3.6
Найти точку пересечения прямой и плоскости.
Задание 3.7
Найти точку , симметричную точке относительно прямой (для вариантов 1-15) или плоскости (для вариантов 16-30).
§5. КРИВЫЕ ВТОРОГО ПОРЯДКА
Пример 3.9
Какое геометрическое место точек определяет уравнение
?
Решение:
Разделим обе части уравнения на 3 и, дополняя до полных квадратов, находим
или
.
Сравнивая полученное
уравнение с уравнением
,
которое определяет окружность с центром
в точке
и радиусом
,
заключаем, что
.
Таким образом,
искомое уравнение определяет окружность
с центром в точке
и радиусом
(рис. 2).
|
Рисунок 2
Ответ: данное уравнение определяет окружность с центром в точке и радиусом .
Пример 3.10
Определить вид и
расположение на плоскости линии
.
Решение:
Преобразуем левую часть уравнения, выделяя полные квадраты:
или
.
Разделим обе части на 36:
.
Сравнивая полученное
уравнение с уравнением
,
которое определяет гиперболу с центром
в точке
и полуосями
и
,
заключаем, что искомое уравнение
определяет гиперболу с центром в точке
и полуосями
(рис. 3).
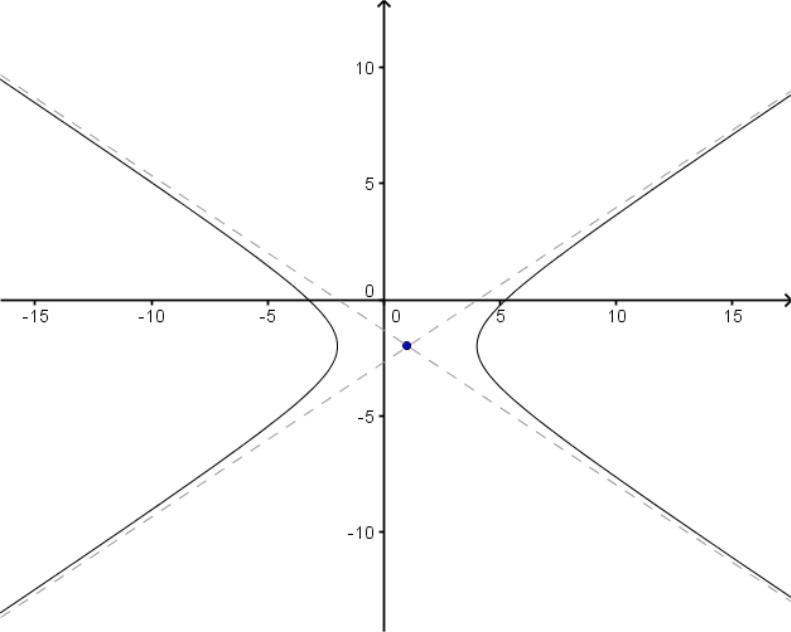
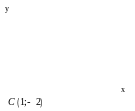
Рисунок 3
Ответ: данное уравнение определяет гиперболу с центром в точке и полуосями .