Задание 5.20.

1.	.	2.	.
3.	.	4.	.
5.	.	6.	.
7.	.	8.	.
9.	.	10.	.
11.	.	12.	.
13.	.	14.	.
15.	.	16.	.
17.	.	18.	.
19.	.	20.	.
21.	.	22.	.
23.	.	24.	.
25.	.	26.	.
27.	.	28.	.
29.	.	30.	.

§ 5. Полное исследование функций

Чтобы построить график функции , необходимо насколько возможно полно исследовать её. Для этого необходимо найти:

1. Область определения функции.

2. Точки разрыва функции.

Точкой разрыва функции называется такая точка , в которой:

• либо не определена функция;

• либо не существует ;

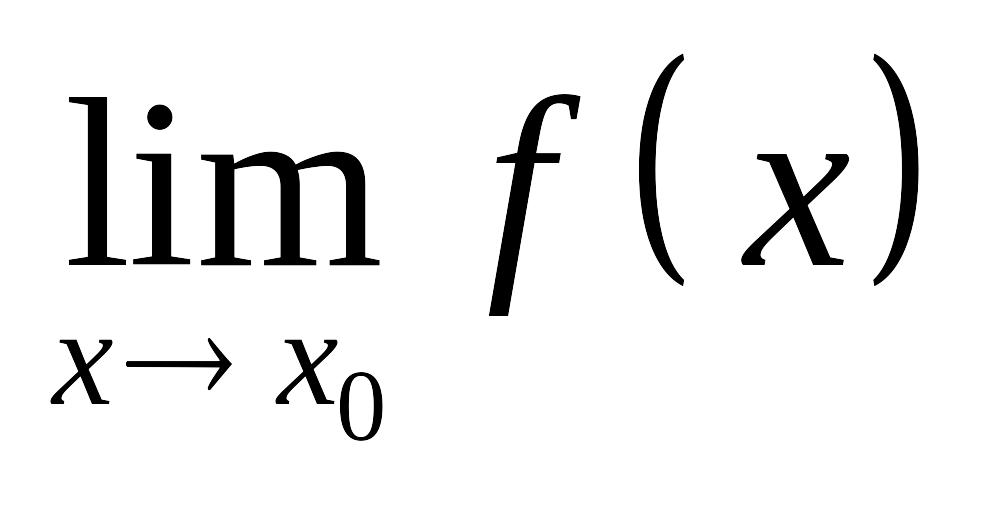• либо .

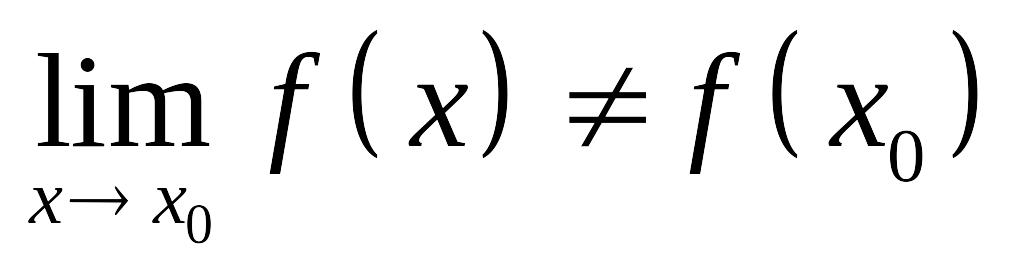3. Точки пересечения графика функции с координатными осями.

4. Исследовать четность функции. При этом, если функция чётная, т.е. 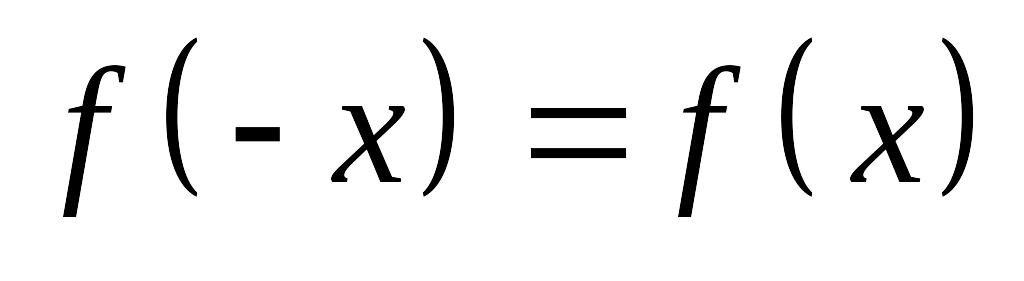, то график функции симметричен относительно оси ординат; если функция нечётная, т.е. , то график функции симметричен относительно начала координат.

5. Точки экстремумов, интервалы возрастания и убывания функции, экстремумы функции.

Необходимое условие существования экстремума в точке: если функция имеет в точке экстремум – max (min), то её производная в этой точке обращается в нуль .

Точки, в которых производная равна нулю или не существует, называют критическими. Не во всех критических точках может существовать экстремум. Исследование функции в критических точках состоит из проверки достаточных условий существование экстремума: пусть функция непрерывна и имеет конечную производную в некоторой окрестности точки . Если при переходе слева направо через точку производная меняет знак «плюс» на «минус», то в точке функция имеет максимум. Если при переходе слева направо через точку производная меняет знак «минус» на «плюс», то в точке функция имеет минимум. Если при переходе через не меняет знак, то в точке экстремума нет.

Для того чтобы функция непрерывная на отрезке была монотонно убывающей на интервале , необходимо и достаточно выполнение условия на .

Для того чтобы функция непрерывная на отрезке была монотонно возрастающей на интервале , необходимо и достаточно выполнение условия на .

6. Точки перегиба, интервалы выпуклости и вогнутости графика функции.

Если в точке вторая производная обращается в нуль или не существует и при переходе через точку меняет знак, то точке существует перегиб, если же знака не меняет, то перегиба нет.

Для того чтобы функция на была выпуклой необходимо и достаточно, чтобы внутри отрезка выполнялось условие ; а чтобы функция была вогнутой на необходимо и достаточно, чтобы внутри отрезка выполнялось условие .

7. Асимптоты кривой.

Если расстояние от точки кривой до некоторой определённой прямой по мере удаления точки в бесконечность стремится к нулю, то эта прямая называется асимптотой кривой. Будем различать вертикальные, наклонные и горизонтальные асимптоты.

1. Вертикальные асимптоты. Из определения асимптоты следует, что если

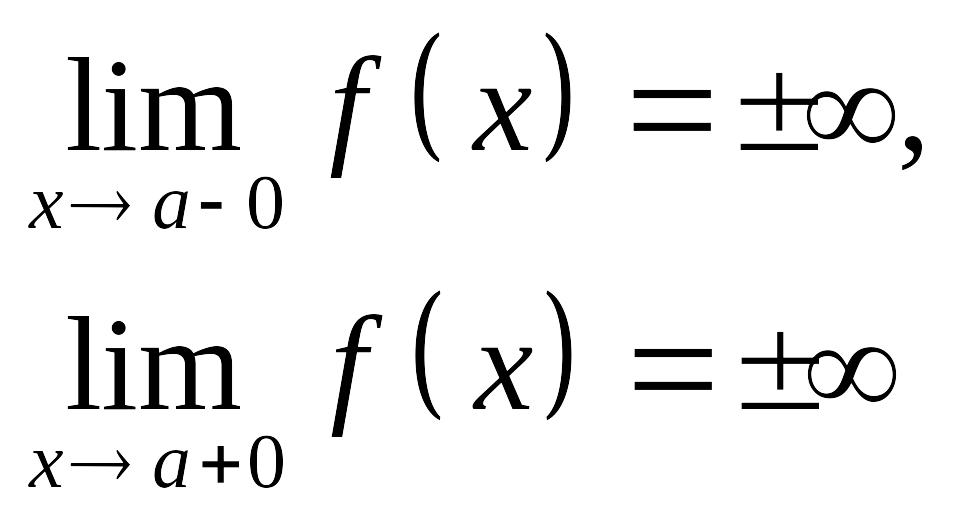
или

,

то прямая есть асимптота кривой ; и обратно, если прямая есть асимптота, то выполняется одно из написанных равенств.

2. Наклонные асимптоты.

Кривая имеет наклонную асимптоту, уравнение которой имеет вид

,

где

.

Если , то наклонных асимптот нет.

3. Горизонтальные асимптоты.

Кривая имеет горизонтальную асимптоту, уравнение которой имеет вид

,

где

.

8. Согласно проведенному исследованию построить график функции.
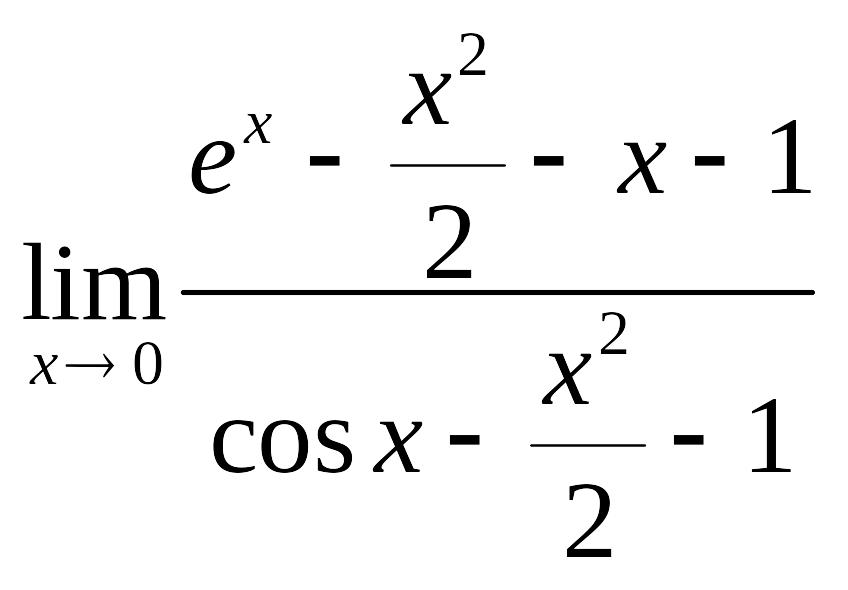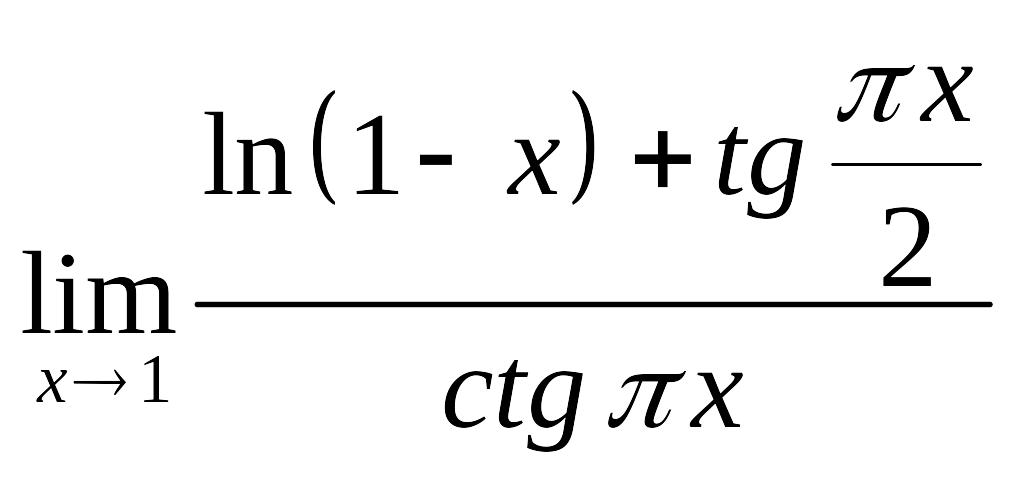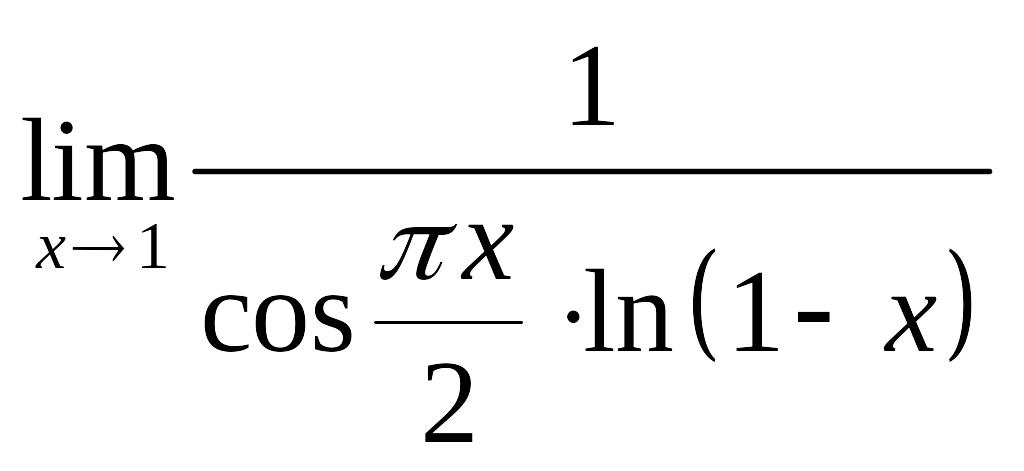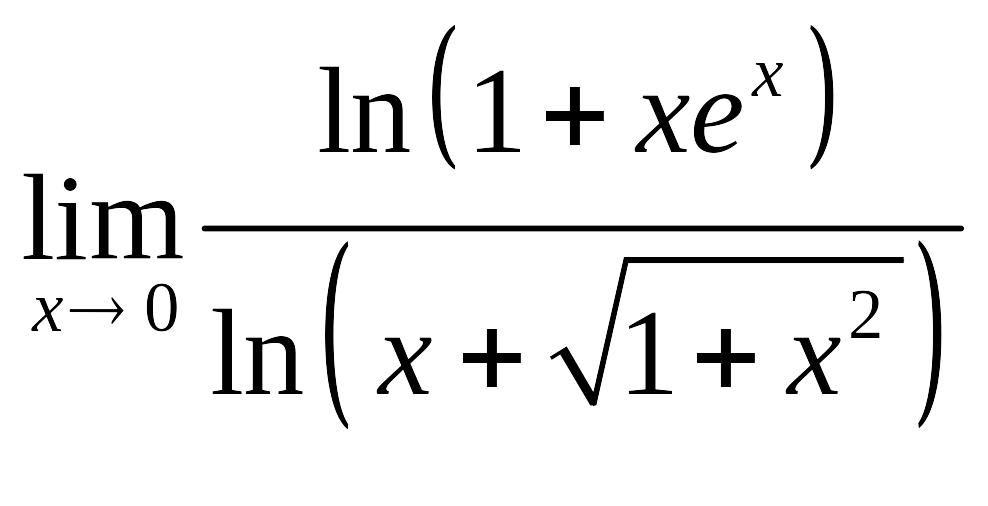