
- •Часть 1
- •Введение
- •Глава 1 элементы линейной алгебры §1. Определители Пример 1.1.
- •Пример 1.4.
- •Пример 1.5.
- •Пример 1.6.
- •Пример 2.2
- •Пример 2.3
- •Пример 2.4
- •Пример 2.5
- •Задания для самостоятельного решения. Задание 2.1. Написать разложение вектора по векторам
- •Задание 2.2. Найти косинус угла между векторами и
- •Задание 2.3 Вычислить площадь параллелограмма, построенного на векторах и
- •Задание 2.4. Определить коллинеарны ли векторы и , построенные по векторам и ?
- •Задание 2.5. Вычислить объем тетраэдра с вершинами в точках и его высоту, опущенную из вершины на грань .
- •Глава 3 элементы аналитической геометрии §1. Прямая на плоскости Пример 3.1
- •Задания для самостоятельного решения. Задание 3.1.
- •§2. Плоскость в пространстве Пример 3.2
- •Пример 3.7
- •Пример 3.8
- •Пример 3.10
- •Пример 3.11
- •Пример 3.12
- •Пример 3.13
- •Пример 3.14
- •Глава 4 введение в анализ § 1. Пределы числовых последовательностей Пример 4.1
- •Задания для самостоятельного решения. Задание 4.1 Вычислить пределы числовых последовательностей.
- •§ 2. Пределы функций Пример 4.2 Вычислить пределы дробно-рациональных функций:
- •Пример 4.3
- •Задания для самостоятельного решения. Задание 4.2. Вычислить пределы дробно-рациональных функций
- •Задание 4.3. Вычислить пределы иррациональных функций
- •§ 3. Замечательные пределы. Сравнение бесконечно малых. Пример 4.4
- •Пример 4.5
- •Пример 4.6
- •Задания для самостоятельного решения. Задание 4.4. Вычислить пределы, используя первый замечательный предел и его следствия.
- •Задание 4.5. Вычислить пределы, используя второй замечательный предел и его следствия.
- •Задание 4.6 Определить порядок относительно данной функции, бесконечно малой при .
- •§ 4. Непрерывность функций Пример 4.7
- •Пример 4.8
- •Задания для самостоятельного решения. Задание 4.7. Установить, является ли данная функция непрерывной или разрывной для каждого из данных значений . Сделать схематический чертёж.
- •Пример 5.1
- •Пример 5.2
- •Задание 5.2.
- •Задание 5.3.
- •Задание 5.4.
- •Задание 5.5.
- •Задание 5.6.
- •Задание 5.7.
- •Задание 5.8.
- •Задание 5.9.
- •Задание 5.10.
- •Задание 5.11.
- •Задание 5.12.
- •Задание 5.13.
- •Задание 5.15.
- •Задание 5.16
- •§ 3. Дифференцирование функций, заданных неявно и параметрически Пример 5.17
- •Задание 5.18. Найти и для функций, заданных параметрически.
- •§4. Правило лопиталя Пример 5.19
- •Пример 5.20
- •Задания для самостоятельного решения. Найти указанные пределы, используя правило Лопиталя. Задание 5.19
- •Задание 5.20.
- •§ 5. Полное исследование функций
- •Пример 5.21
- •Пример 5.22
- •Пример 5.23
- •По данным исследования построим график функции .
- •Задания для самостоятельного решения. Провести полное исследование функций и построить их графики Задание 5.21.
- •Задание 5.22.
- •Задание 5.23.
- •§ 6. Применение дифференциала для приближенного вычисления Пример 5.24
- •Пример 5.25
- •Задание 5.25.
- •Литература
- •Содержание
- •Часть 1.
Глава 1 элементы линейной алгебры §1. Определители Пример 1.1.
Для данного
определителя
![]() найти миноры и алгебраические дополнения
для элементов
найти миноры и алгебраические дополнения
для элементов
![]() .
Вычислить определитель
:
.
Вычислить определитель
:
а) разложив его по элементам первой строки;
б) разложив его по элементам третьего столбца;
в) получив предварительно нули в четвертом столбце.
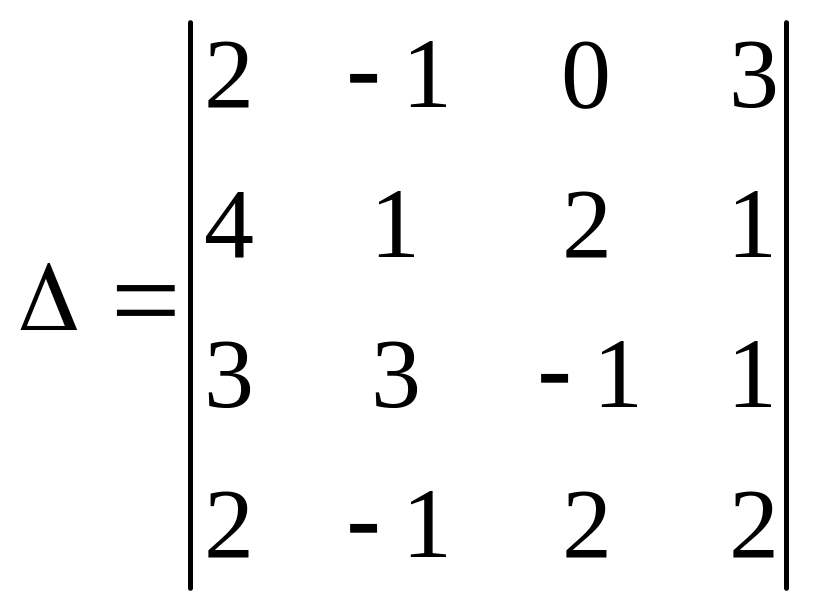
Решение:
Минором элемента
![]() определителя
определителя
![]() -го
порядка называется определитель (
-го
порядка называется определитель (![]() )-го
порядка, полученный из исходного путем
вычеркивания
)-го
порядка, полученный из исходного путем
вычеркивания
![]() -ой
строки и
-ой
строки и
![]() -го
столбца. Обозначается
-го
столбца. Обозначается
![]() .
Найдем миноры
.
Найдем миноры
![]() для заданных элементов
для заданных элементов
![]() .
.
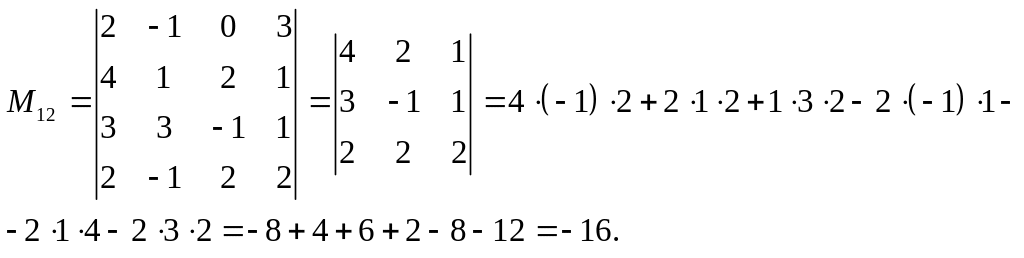



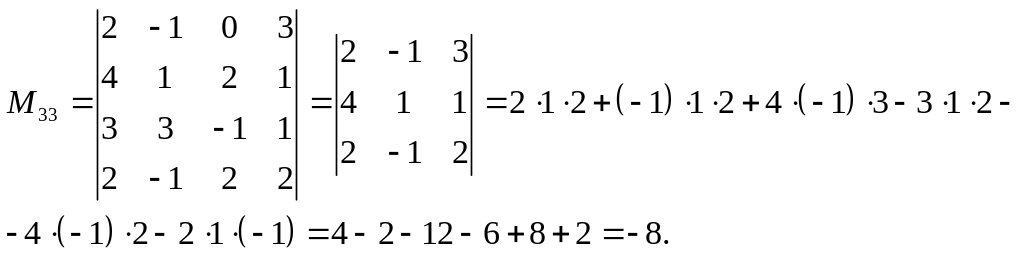
Алгебраическим
дополнением элемента
называется его минор, взятый со знаком
“+”, если сумма
![]() – четная и “-”, если эта сумма нечетная.
Обозначается
– четная и “-”, если эта сумма нечетная.
Обозначается
![]() .
.
![]() .
.
Вычислим
алгебраические дополнения элементов
![]()
![]()
а) Вычисление определителей четвертого порядка и выше удобно проводить, используя свойство: определитель равен сумме произведений элементов любой его строки или столбца на их алгебраические дополнения, то есть
![]() или
или
![]() .
.
Эти формулы
называются разложением определителя
по элементам
![]() ой
строки или
ой
строки или
![]() го
столбца соответственно.
го
столбца соответственно.
Разложим определитель четвертого порядка по элементам первой строки:
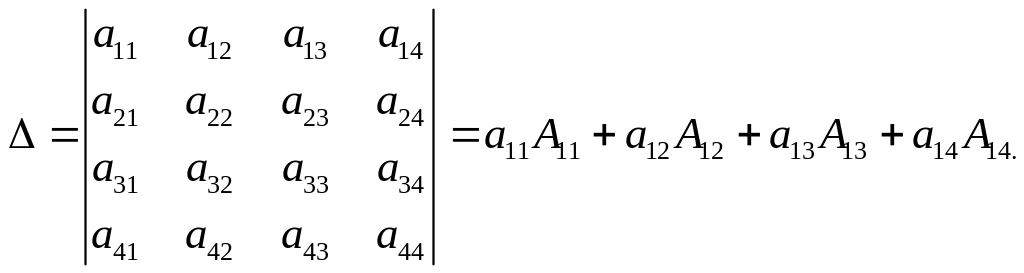
Получим:
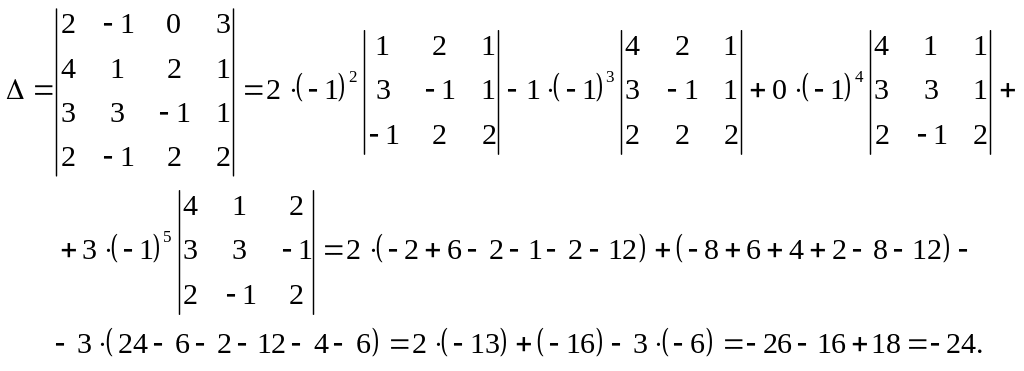
б) Вычислим определитель, разложив его по элементам третьего столбца:
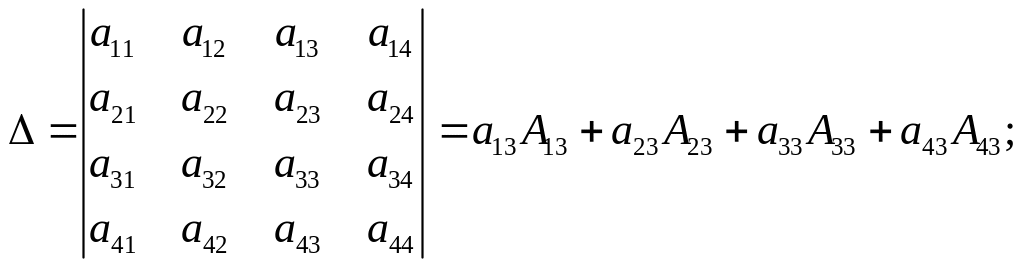
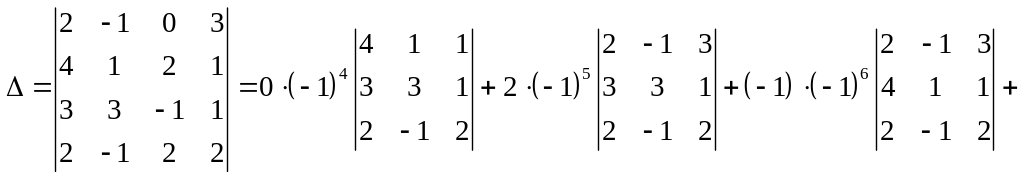
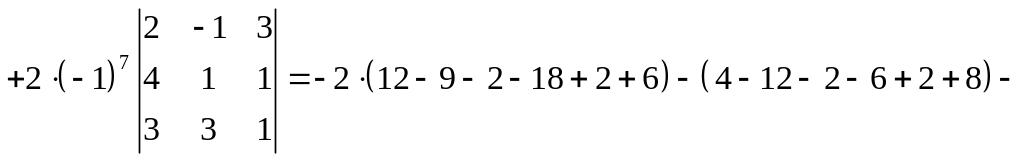
![]()
в) Вычислим определитель, получив предварительно нули в четвертом столбце.
элементы третьей строки (рабочей) перепишем в преобразованный определитель без изменений;
умножим все элементы третьей строки на (-3), прибавим к соответствующим элементам первой строки, а результаты запишем в первую строку преобразованного определителя;
умножим элементы третьей строки на (-1) и прибавим к соответствующим элементам второй строки, результат запишем во вторую строку преобразованного определителя;
умножим все элементы третьей строки на (-2), прибавим к соответствующим элементам четвертой строки, результат запишем в четвертую строку преобразованного определителя.
После этих преобразований значение определителя не изменится, но он примет следующий вид:

Теперь, разложив определитель по элементам четвертого столбца, вычислим его:
![]() ;
;
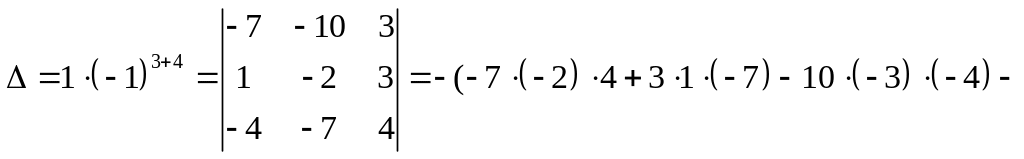
![]()
![]()
![]()
По такой схеме можно вычислить определитель любого порядка.
Ответ:
![]() .
.
Задания для самостоятельного решения.
Задание 1.1.
Для данного определителя
![]() найти миноры и алгебраические дополнения
элементов
найти миноры и алгебраические дополнения
элементов
![]() .
Вычислить определитель
:
.
Вычислить определитель
:
а) разложив его по элементам i-й строки; б) разложив его по элементам j-го столбца; в) получив предварительно нули в i-й строке.
1. 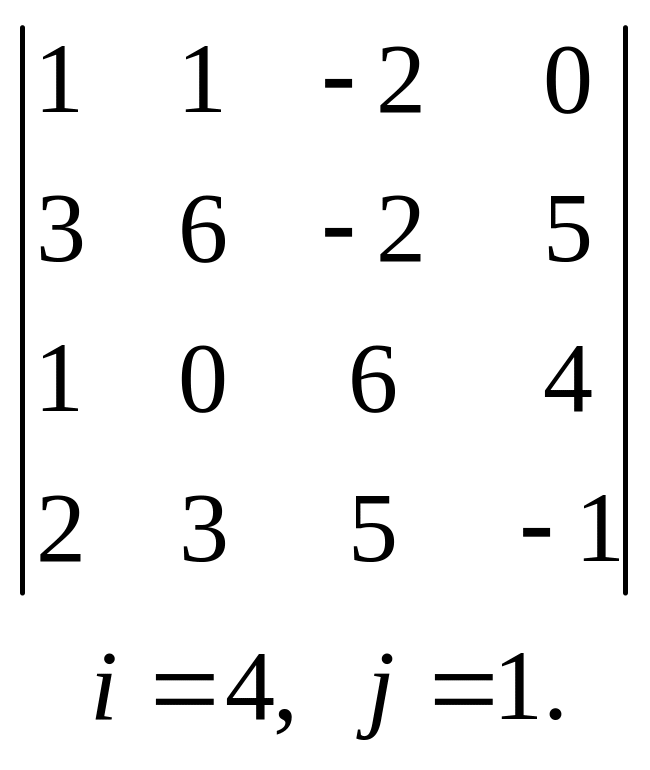 , 2.
, 2.  ,
,
3.  , 4.
, 4. 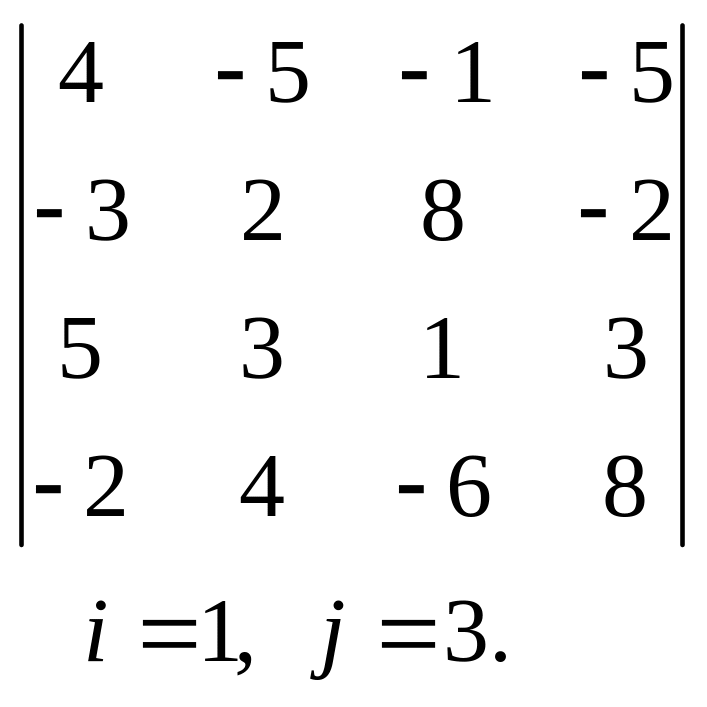 ,
,
5. 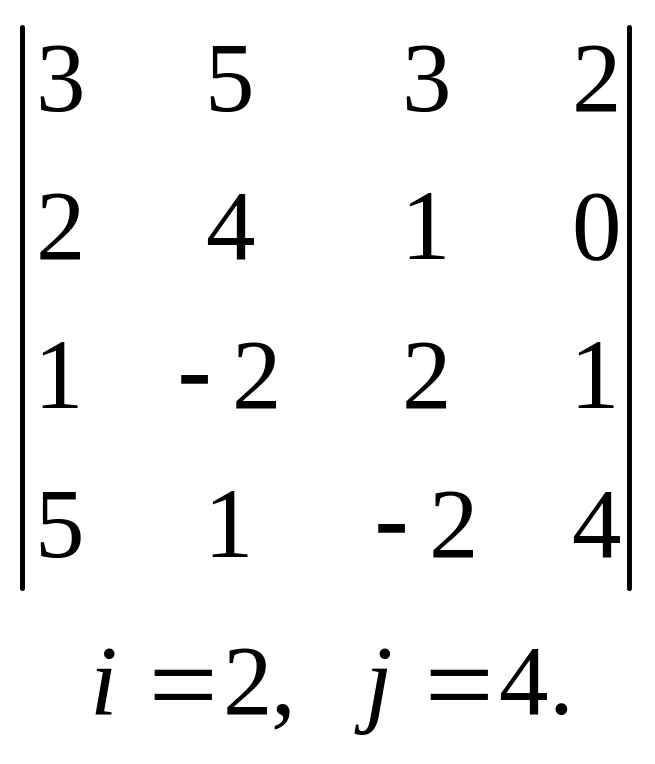 , 6.
, 6. 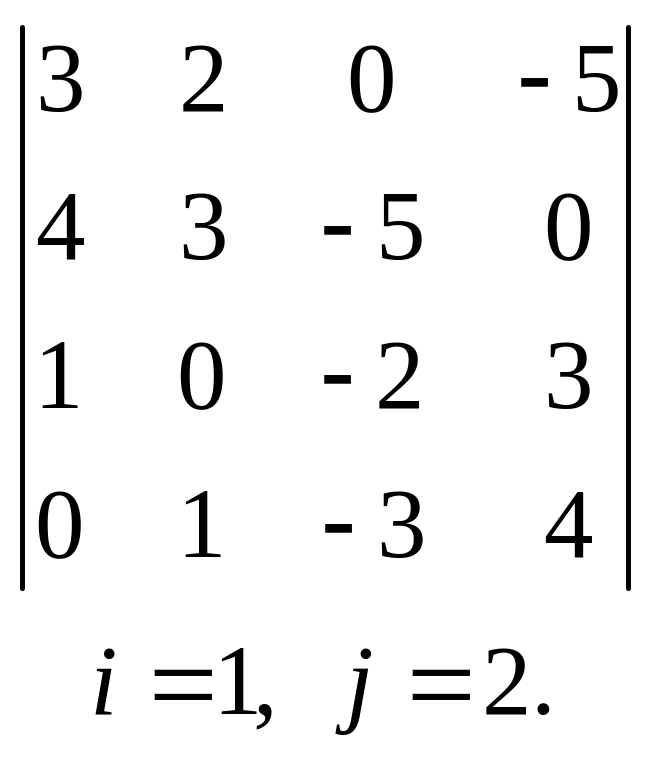 ,
,
7. 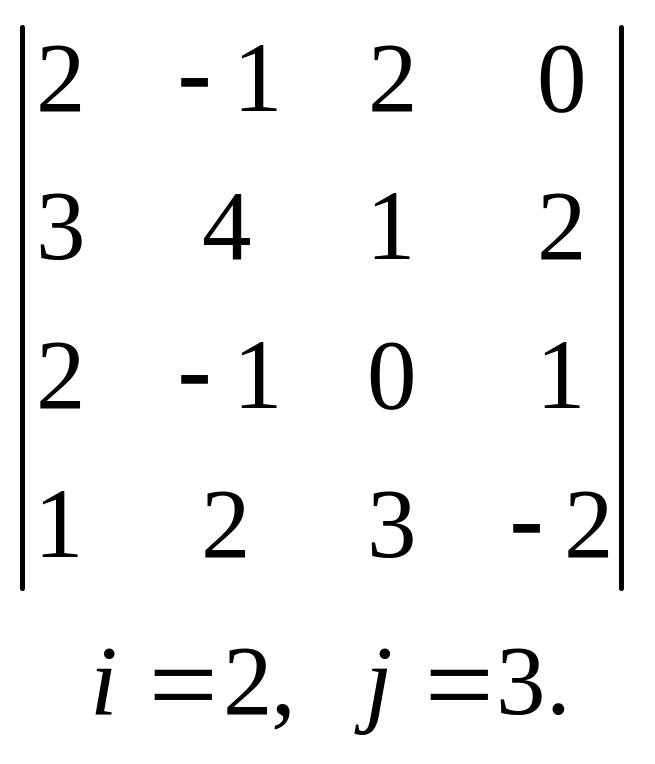 , 8.
, 8. 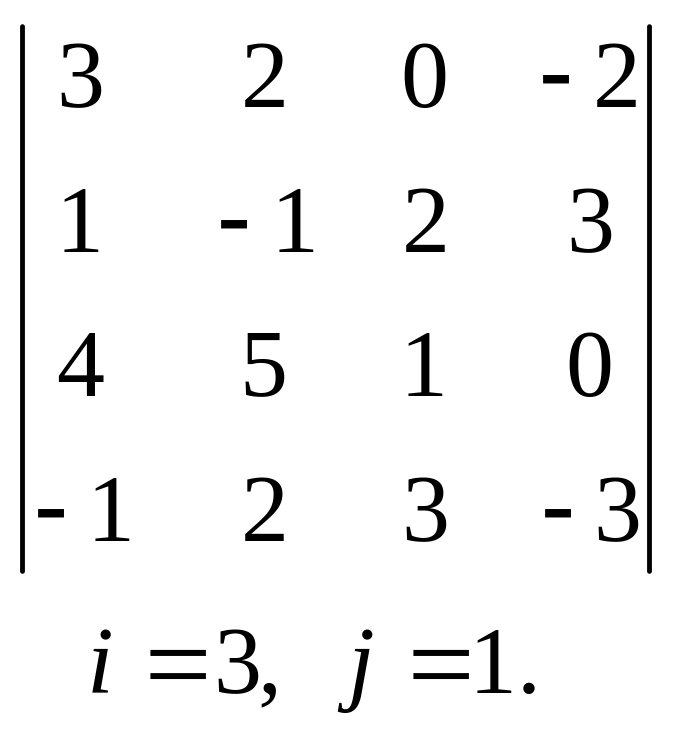 ,
,
9. 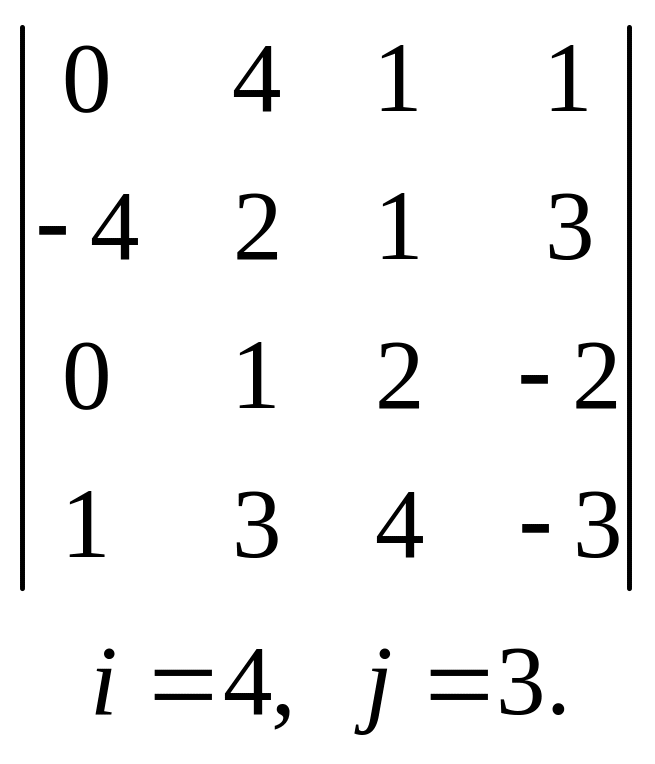 , 10.
, 10. 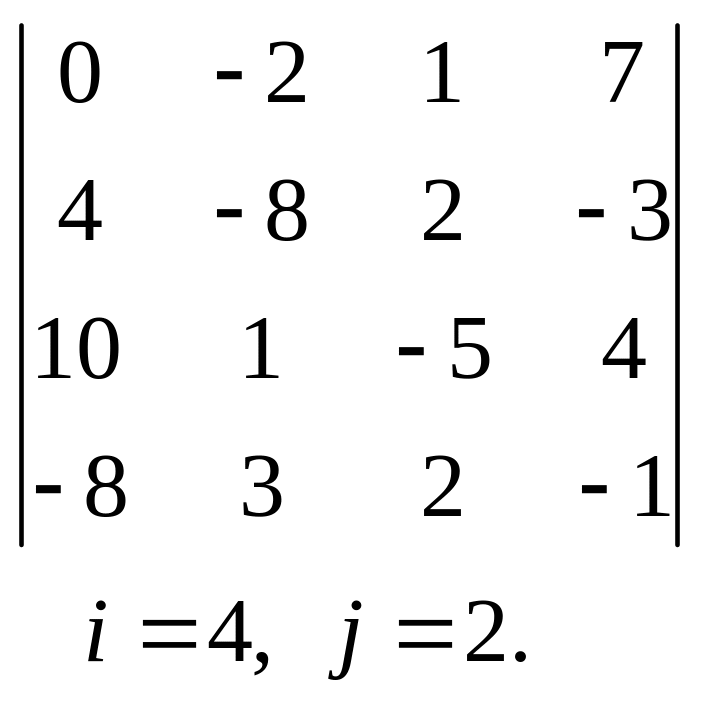 ,
,
11. 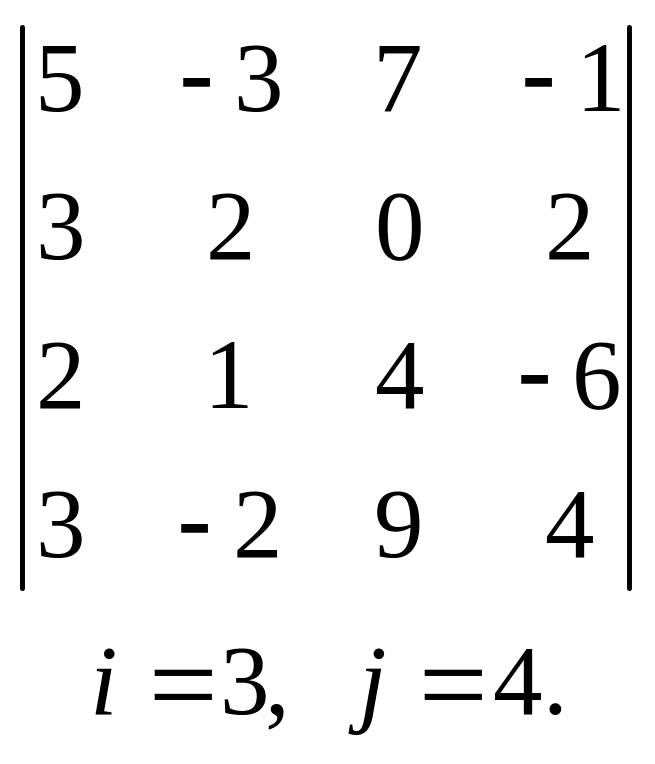 , 12.
, 12. 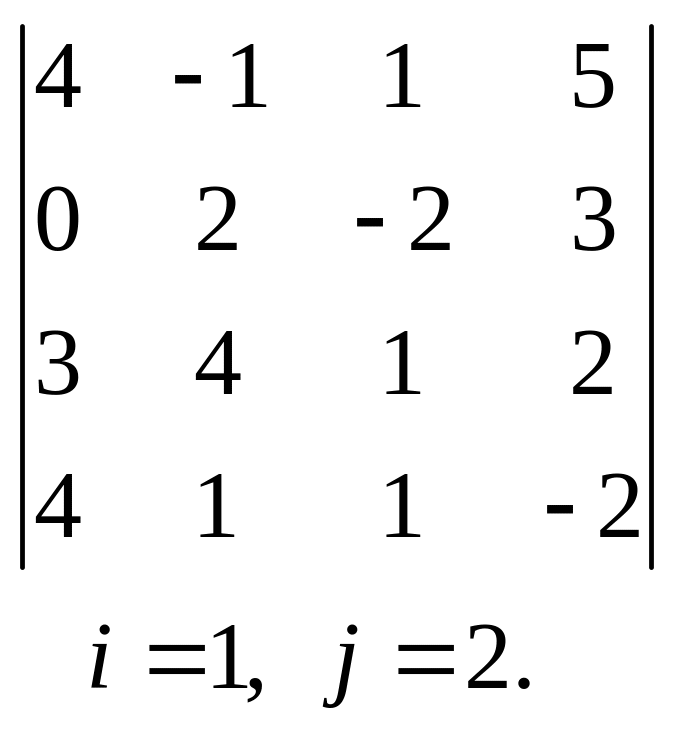 ,
,
13. 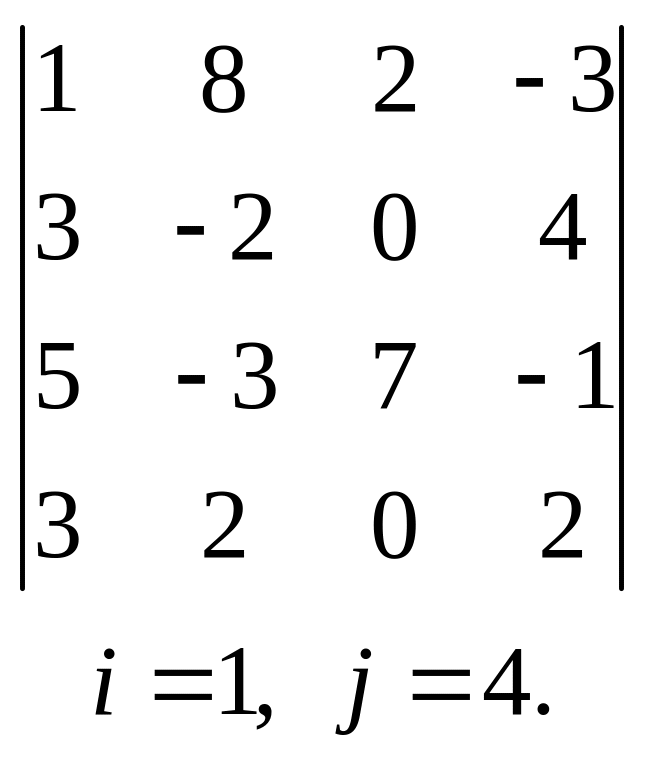 ,
14.
,
14.  ,
,
15.  , 16.
, 16. 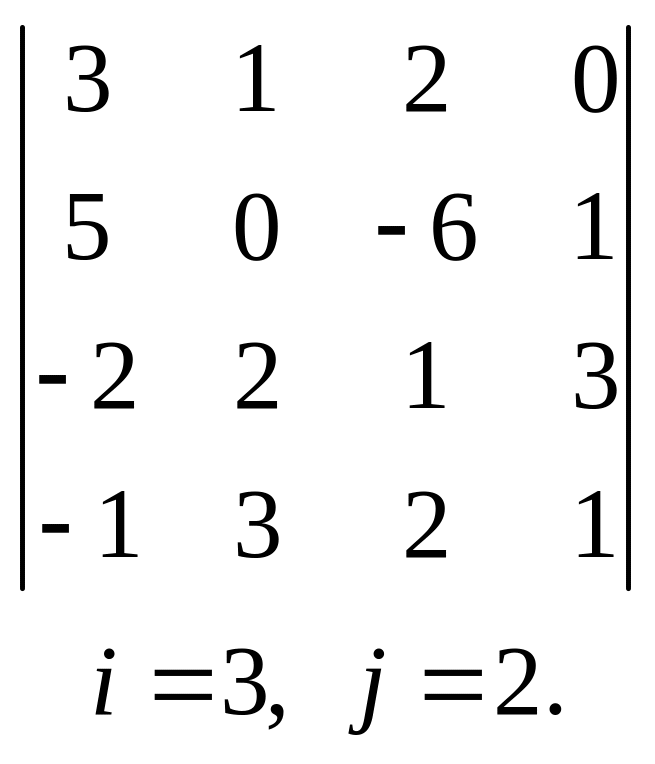 ,
,
17. 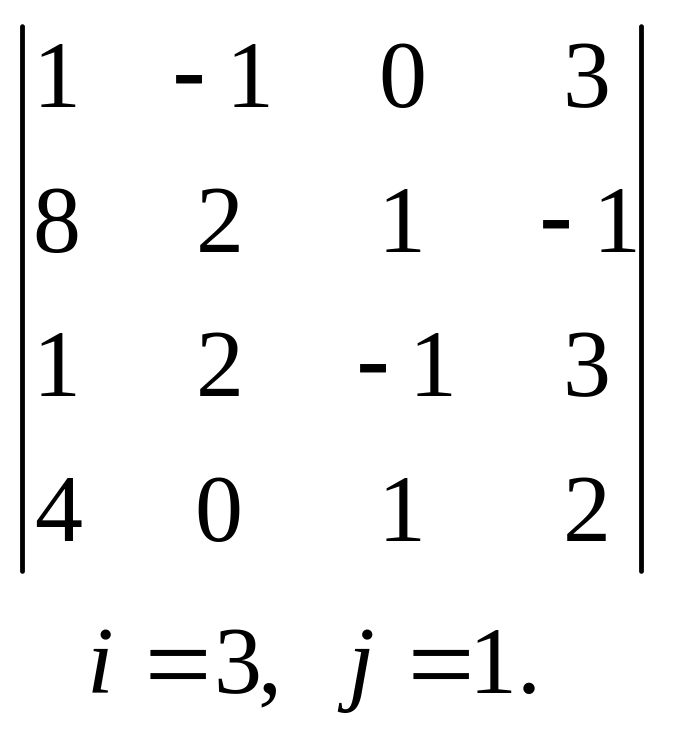 , 18.
, 18.  ,
,
19. 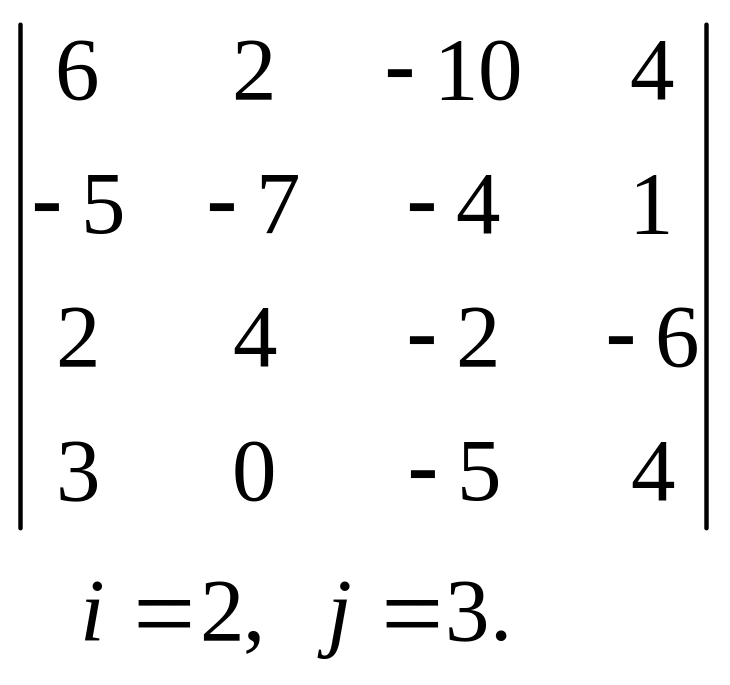 , 20.
, 20. 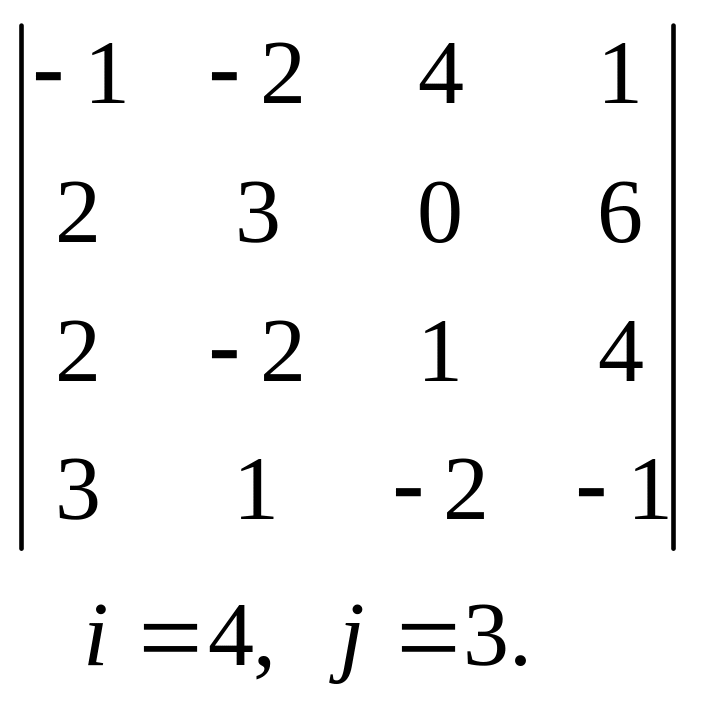 ,
,
21. 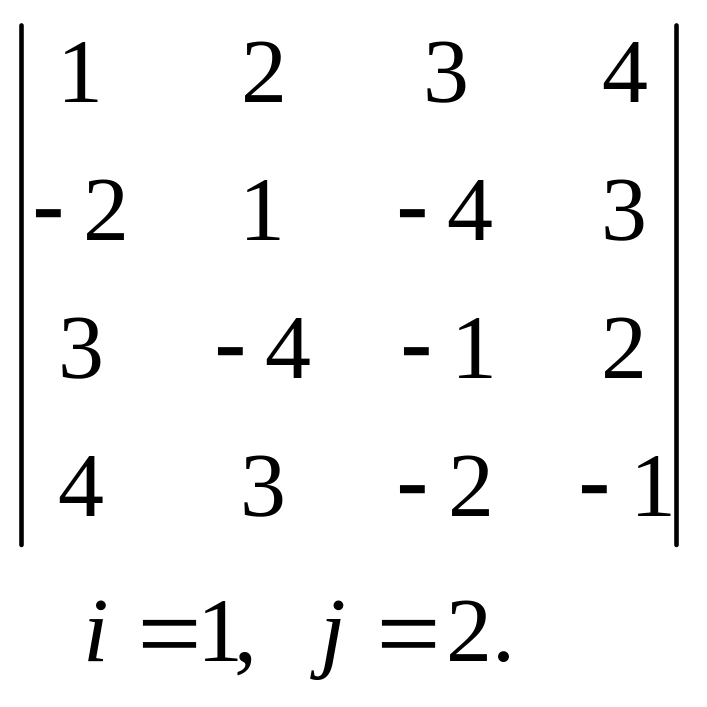 , 22.
, 22. 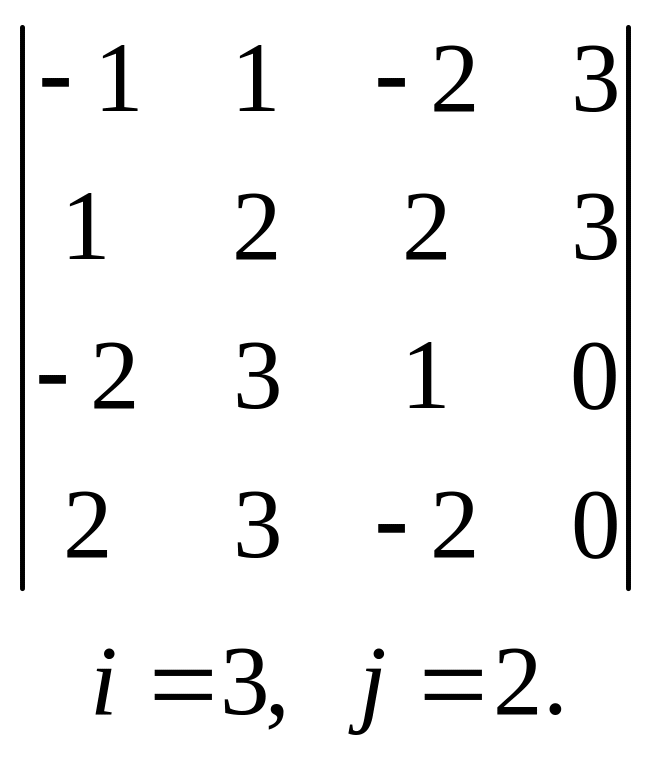 ,
,
23.  , 24.
,
, 24.
,
25. 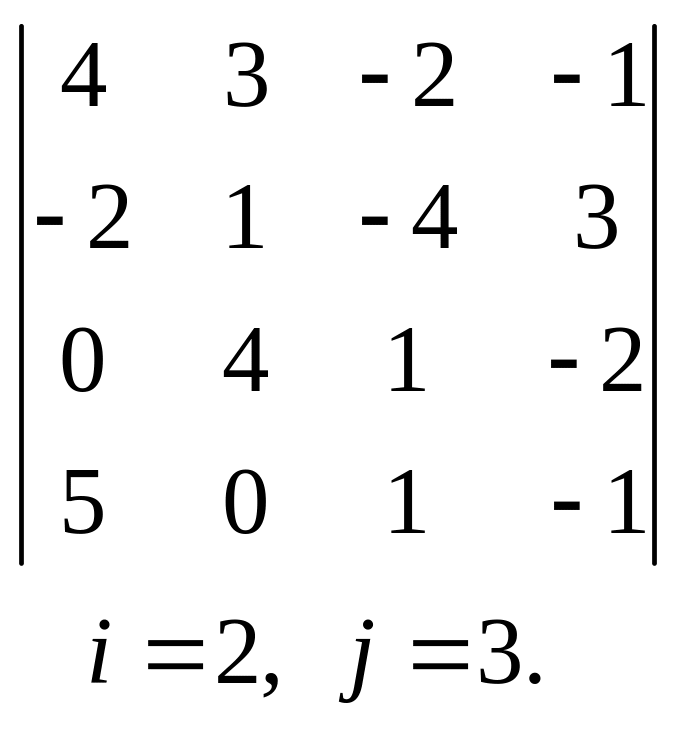 , 26.
, 26. 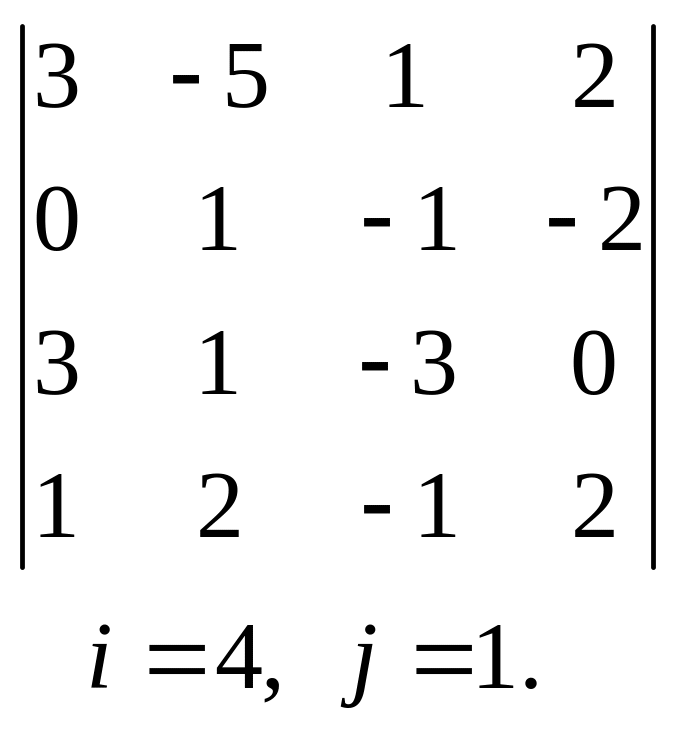 ,
,
27. 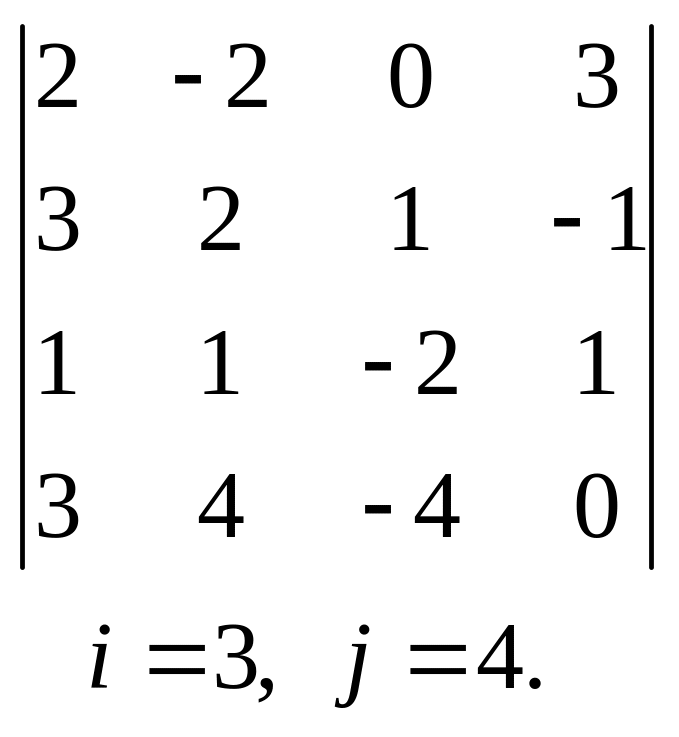 28.
28. 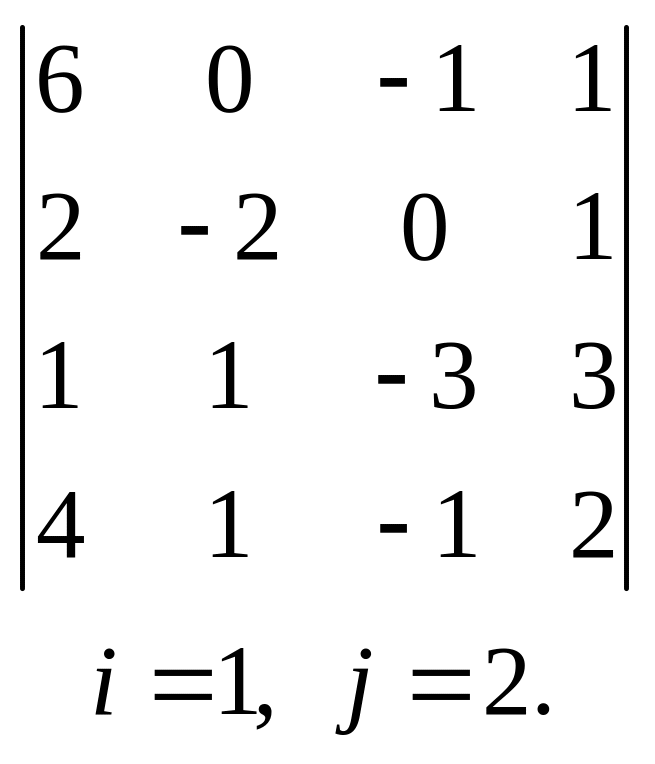 ,
,
29. 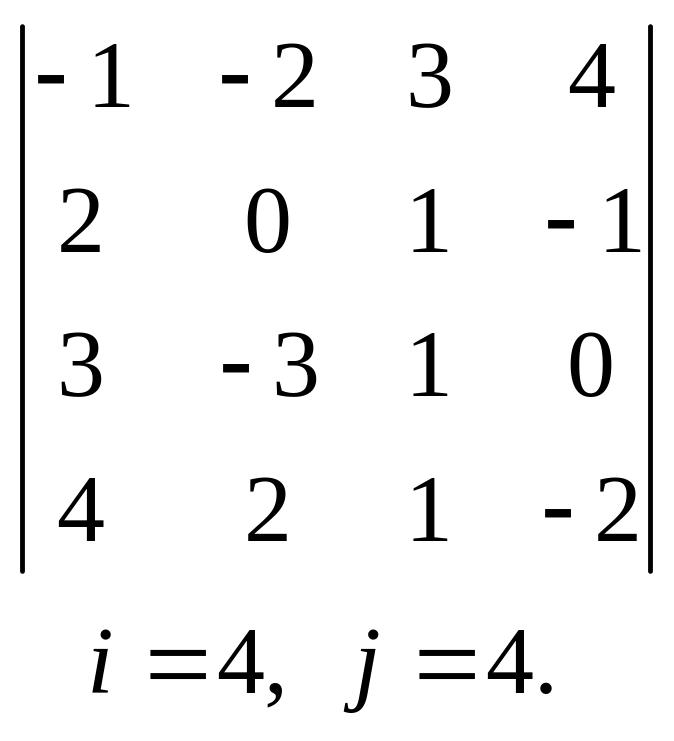 , 30.
, 30. 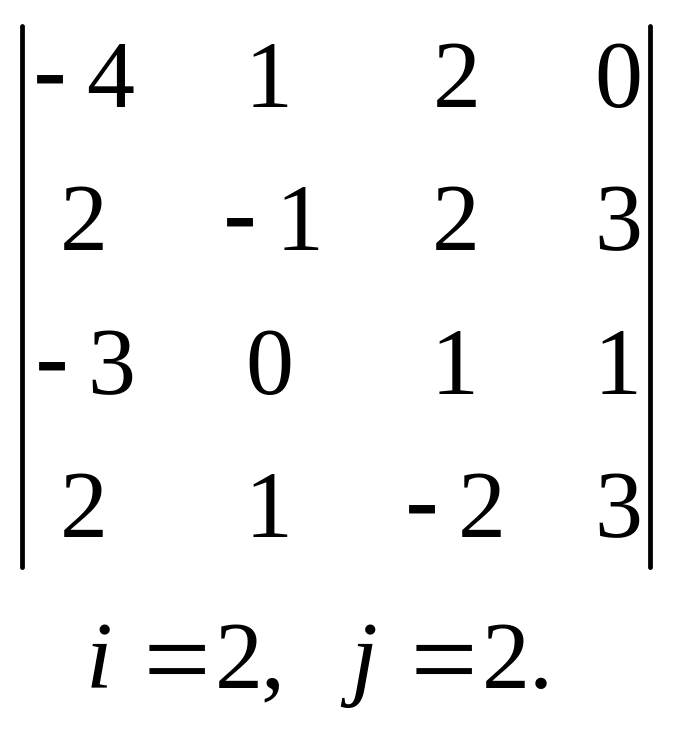 .
.
§2. МАТРИЦЫ
Пример 1.2.
Даны две матрицы
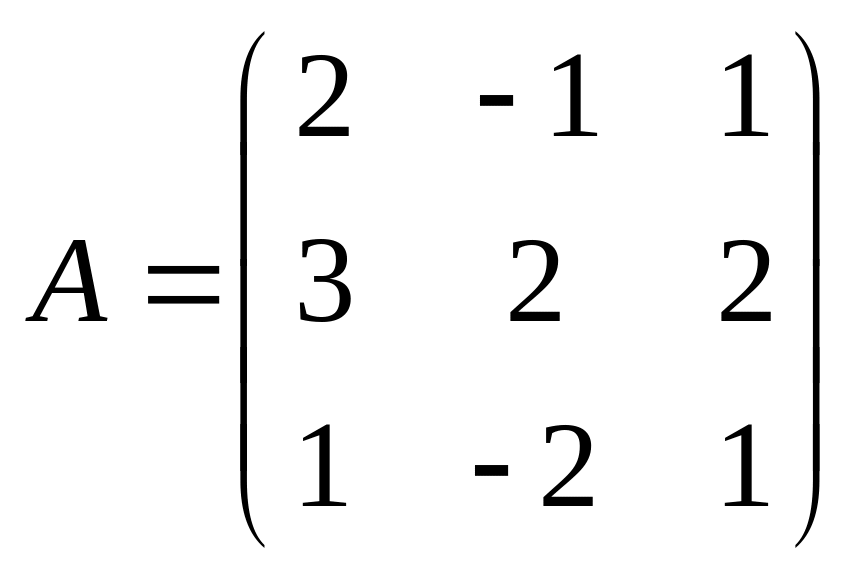 и
и
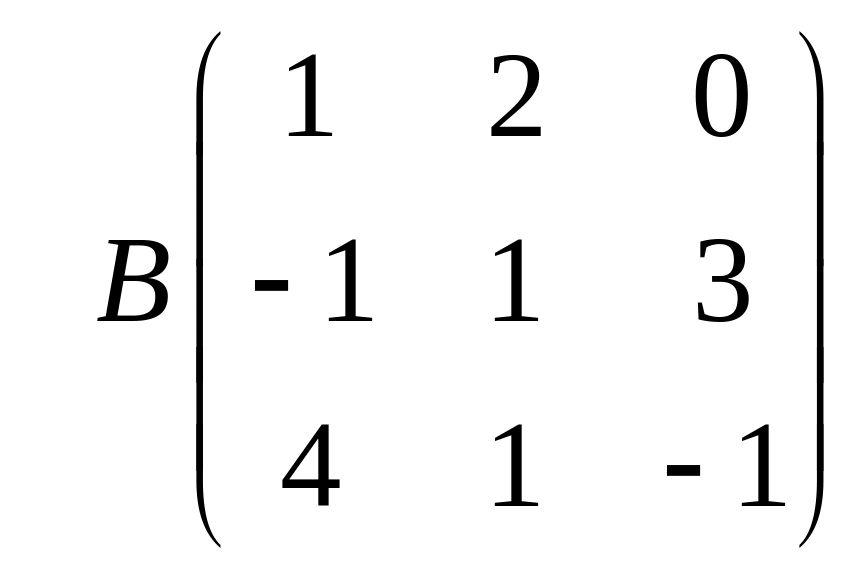 .
.
Найти: а)
![]() ;
б)
;
б)
![]() ;
в)
;
в)
![]() ;
г)
;
г)
![]() ;
д)
;
д)
![]() .
.
Решение:
Операция умножения двух матриц вводится только для случая, когда число столбцов первой матрицы равно числу строк второй матрицы, т.е. для согласованных матриц.
Если матрица
![]() согласованна с матрицей
согласованна с матрицей
![]() ,
то произведением
,
то произведением
![]() матрицы
матрицы
![]() на матрицу
на матрицу
![]() называется такая матрица
называется такая матрица
![]() ,
каждый элемент
,
каждый элемент
![]() которой равен сумме произведений
элементов
ой
строки матрицы
на соответствующие элементы
которой равен сумме произведений
элементов
ой
строки матрицы
на соответствующие элементы
![]() го
столбца матрицы
:
го
столбца матрицы
:
![]() ,
,
![]()
или
![]() .
.
В общем виде
произведение матриц размерности
![]() выглядит следующим образом:
выглядит следующим образом:
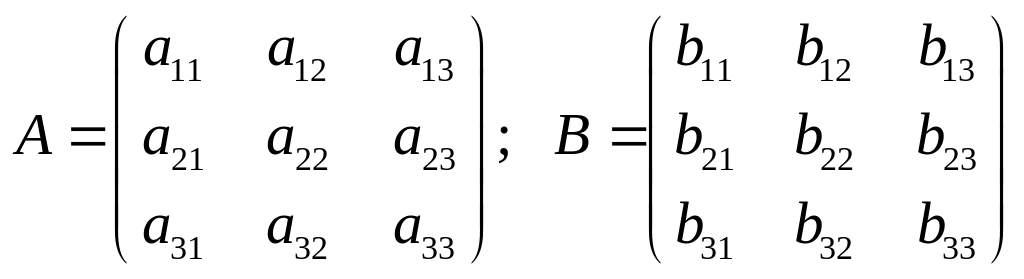
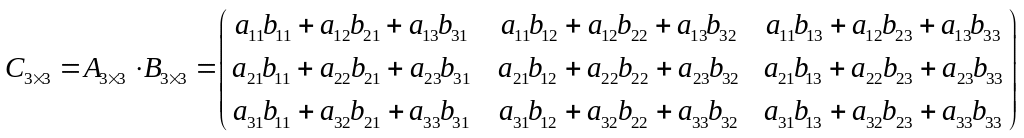
а) ![]()
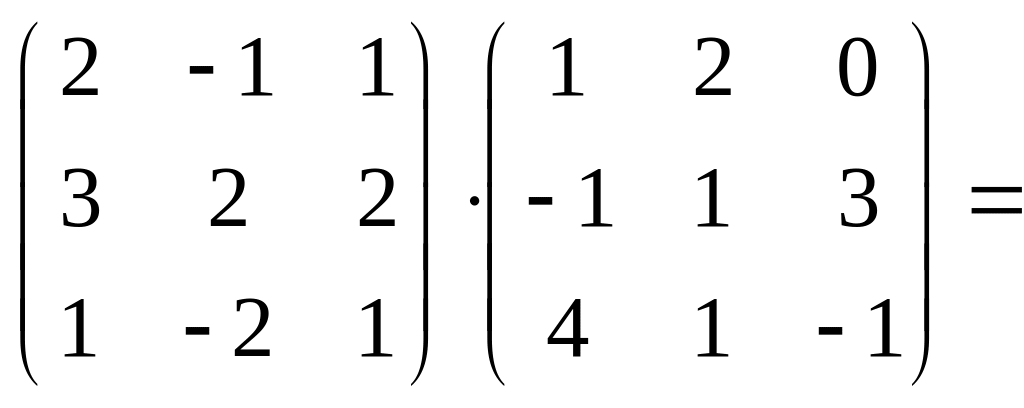
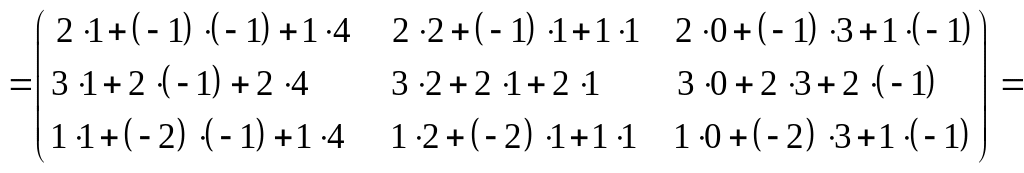
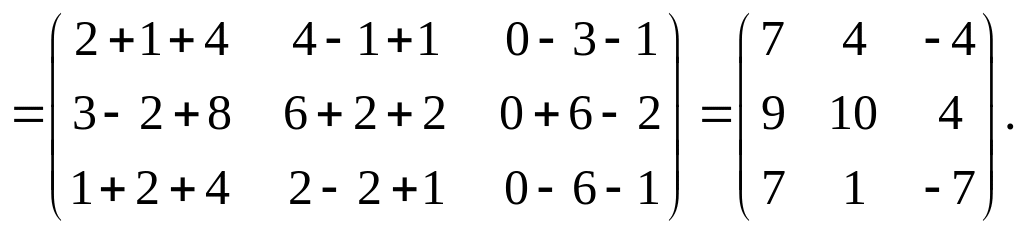
б) 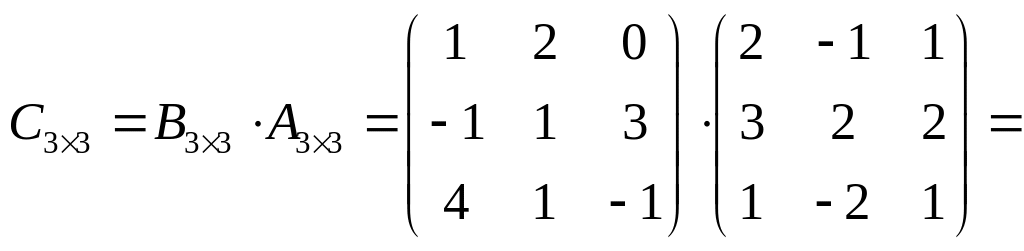
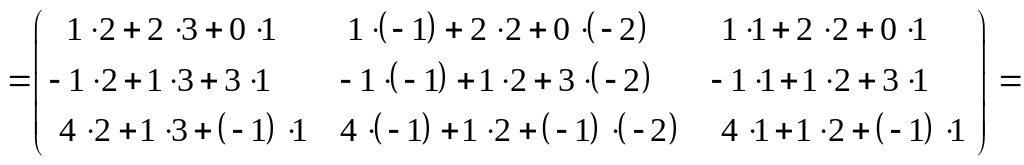
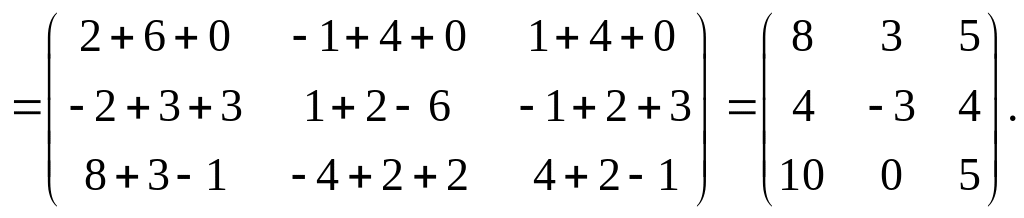
в) Матрица
называется обратной матрице
,
если выполняется условие
![]() ,
где
,
где
![]() - единичная матрица того же порядка, что
и матрица
.
Матрица
имеет ту же размерность, что и матрица
.
- единичная матрица того же порядка, что
и матрица
.
Матрица
имеет ту же размерность, что и матрица
.
Всякая невырожденная квадратная матрица третьего порядка имеет обратную :
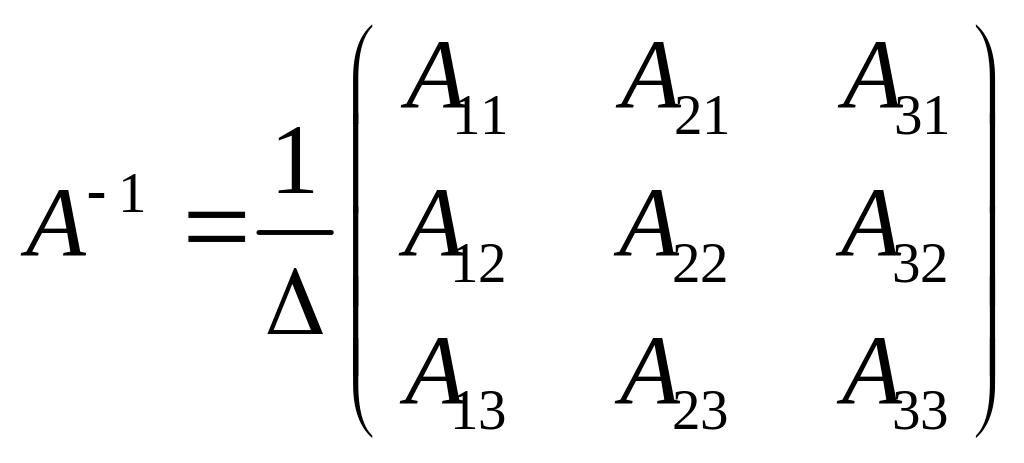 .
.
Вычислим определитель данной матрицы (используем разложение по элементам первой строки):
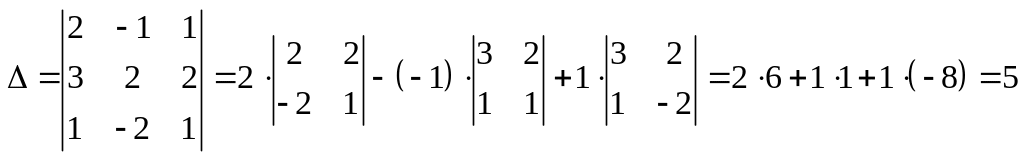 Так
как
Так
как
![]() ,
то матрица
невырожденная и для нее можно составить
обратную
.
,
то матрица
невырожденная и для нее можно составить
обратную
.
Находим алгебраические дополнения:
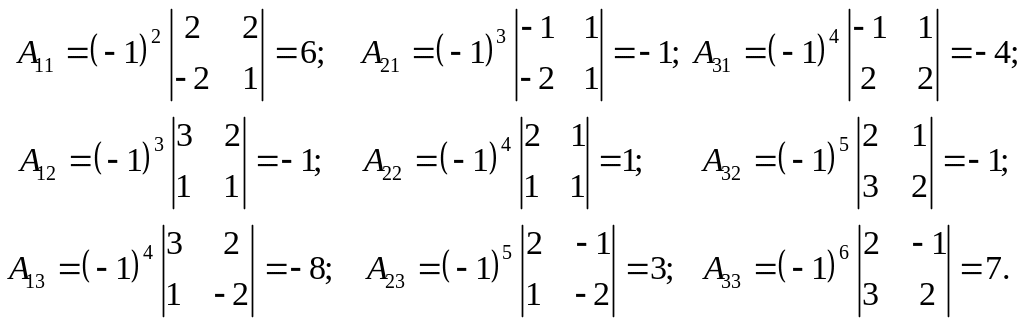
Запишем обратную матрицу :
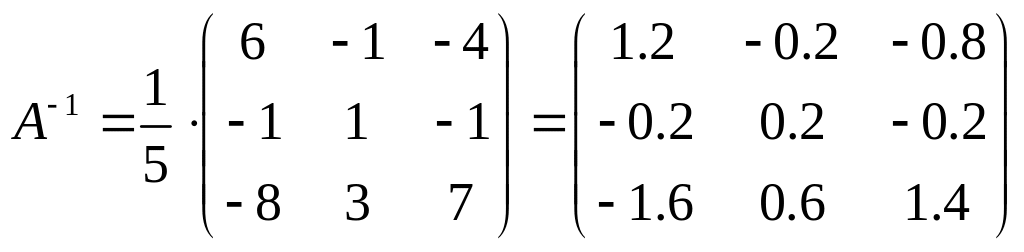 .
.
г) Найдем произведение данной матрицы на обратную :


д) Найдем произведение обратной матрицы на данную :
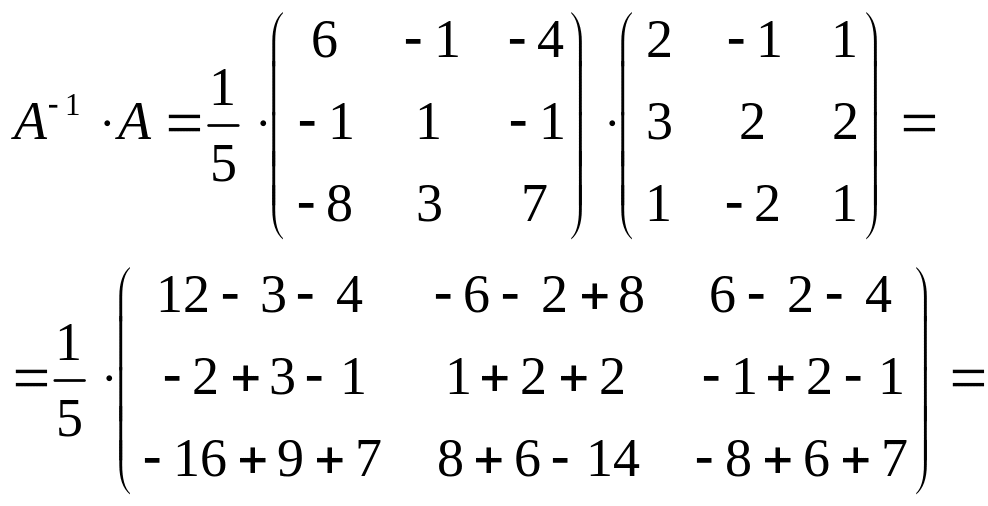
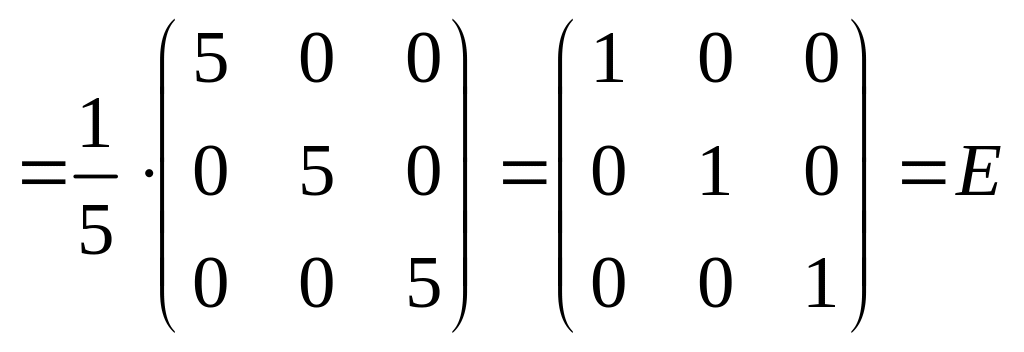 .
.
Так как , то обратная матрица вычислена верно.
Ответ: а)
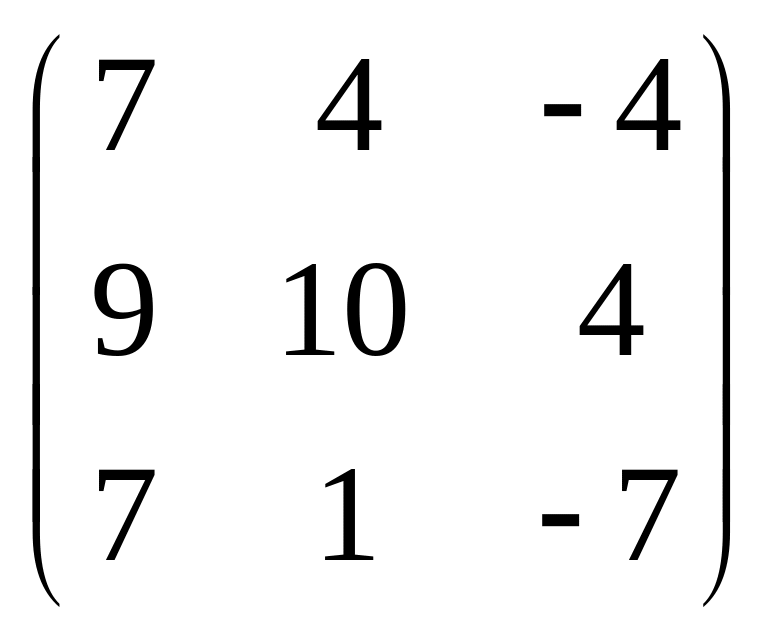 ;
б)
;
б)
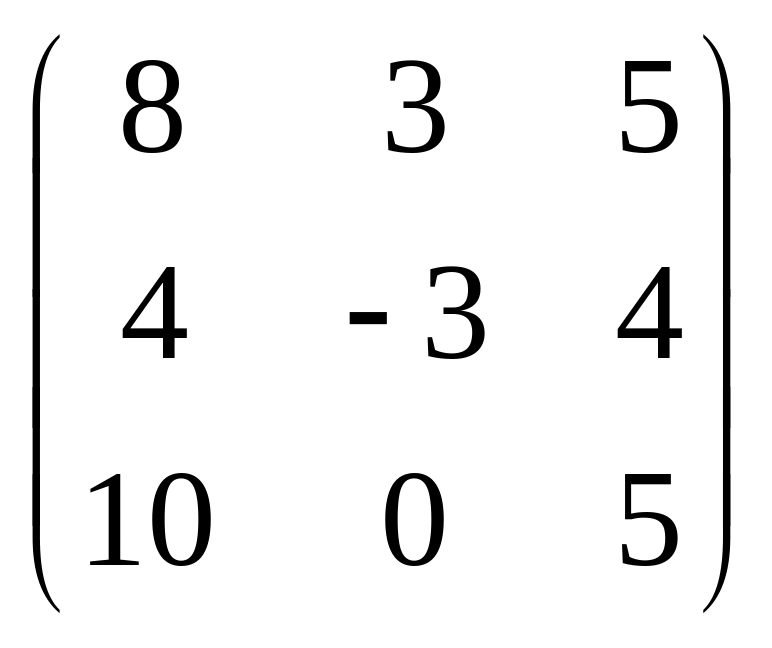 ;
в)
;
в)
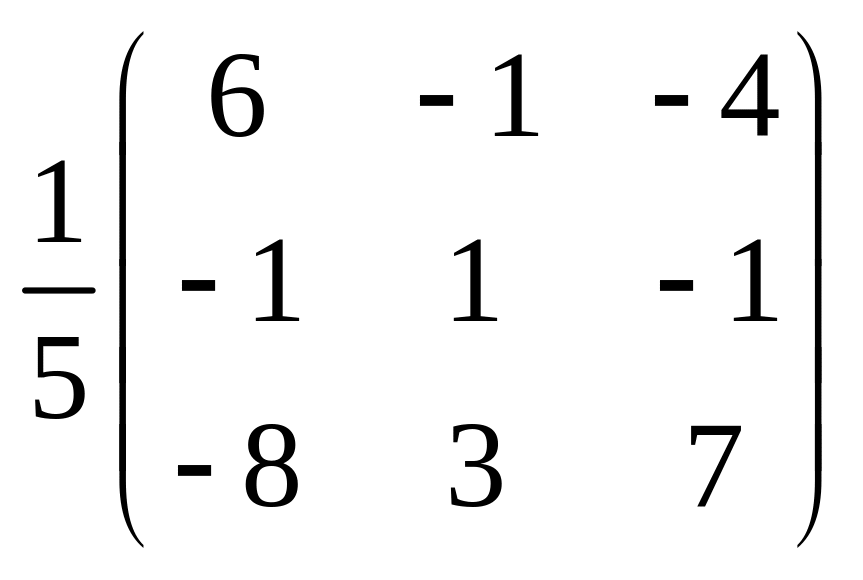 ;
;
г)
 ;
д)
.
;
д)
.
Задания для самостоятельного решения.
Задание 1.2.
Даны две матрицы А и В.
Найти: а) АВ; б) ВА; в)
![]() ;
г)
;
г)
![]() ;
д)
;
д)
![]() .
.
1. 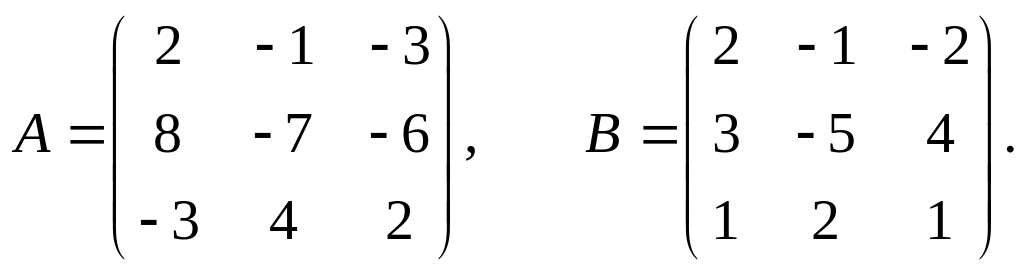
2. 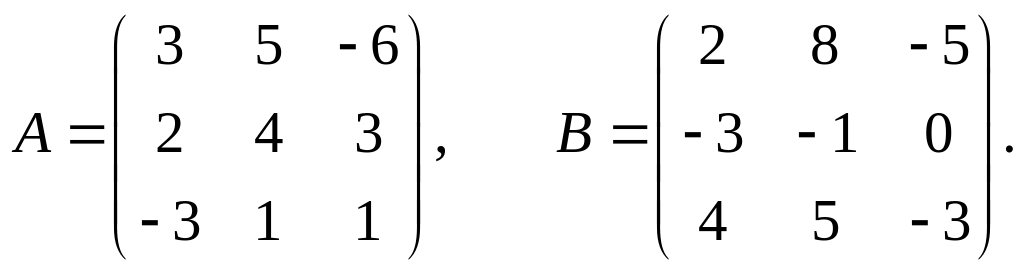
3. 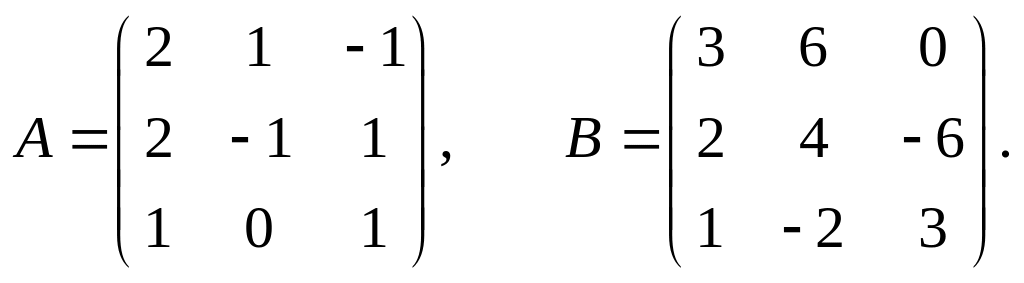
4. 
5.
6. 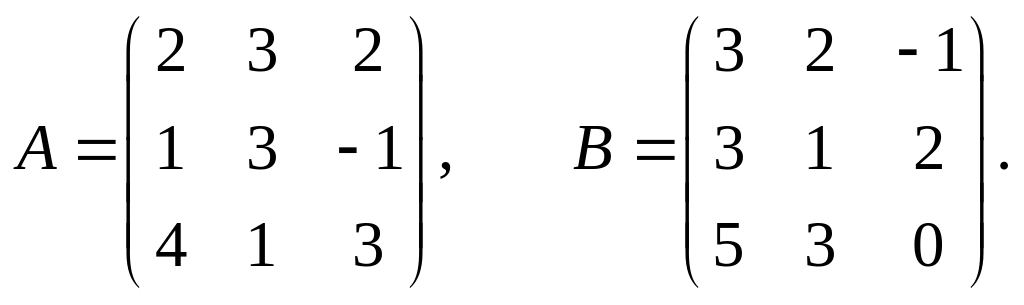
7. 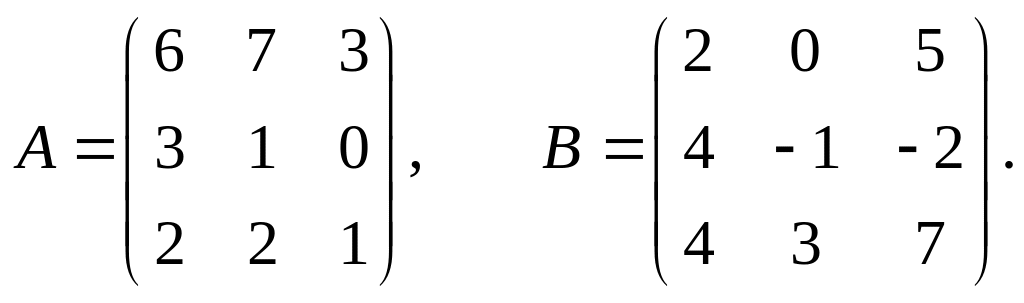
8. 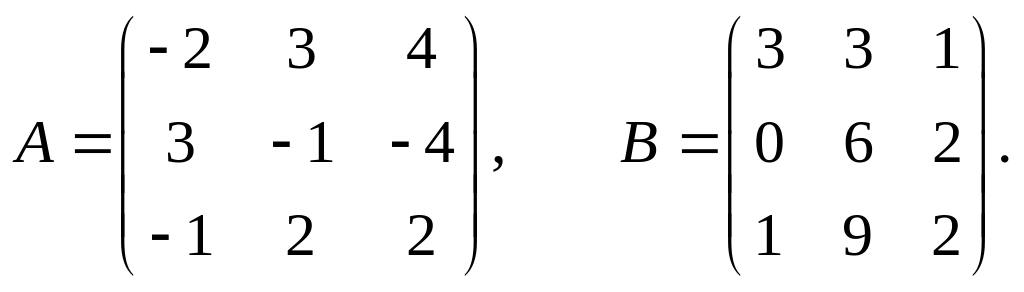
9. 
10. 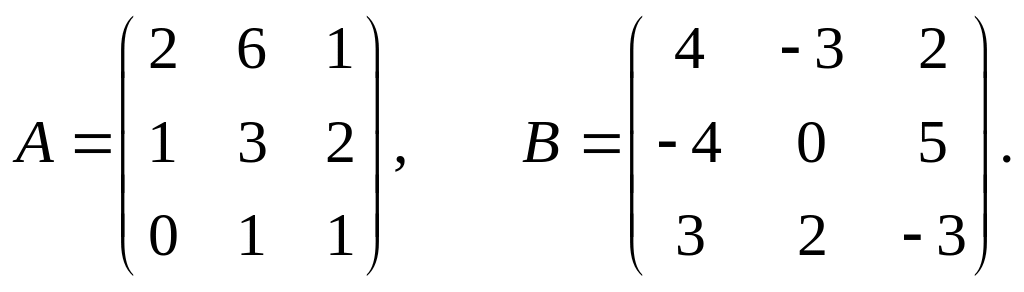
11. 
12. 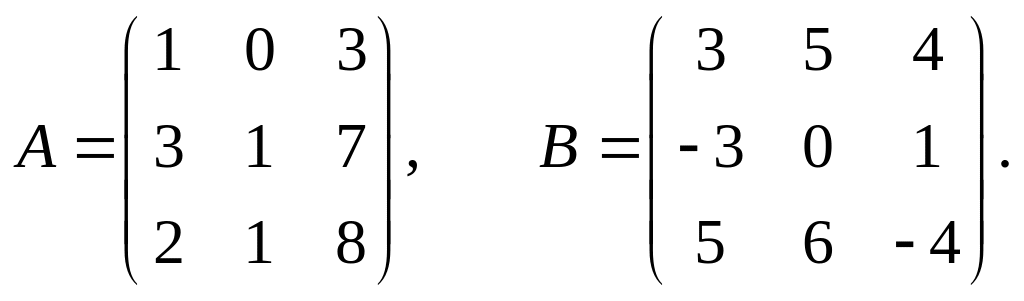
13. 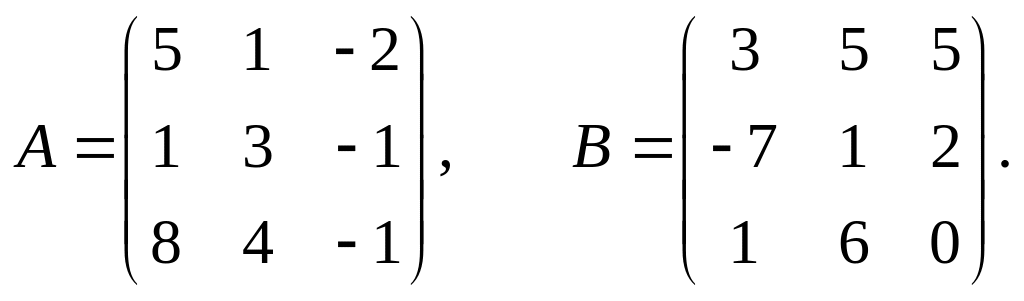
14. 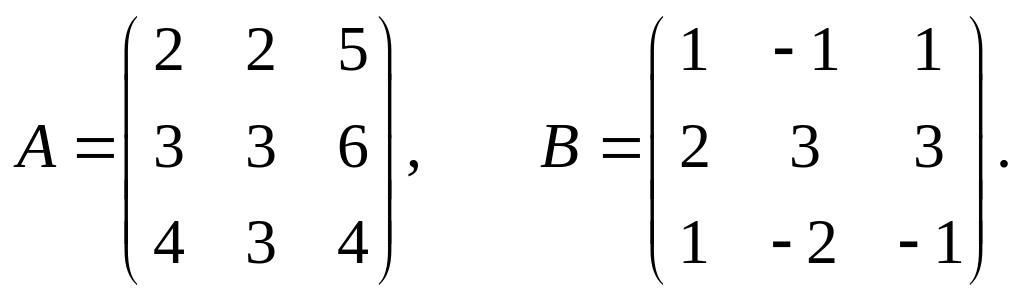
15. 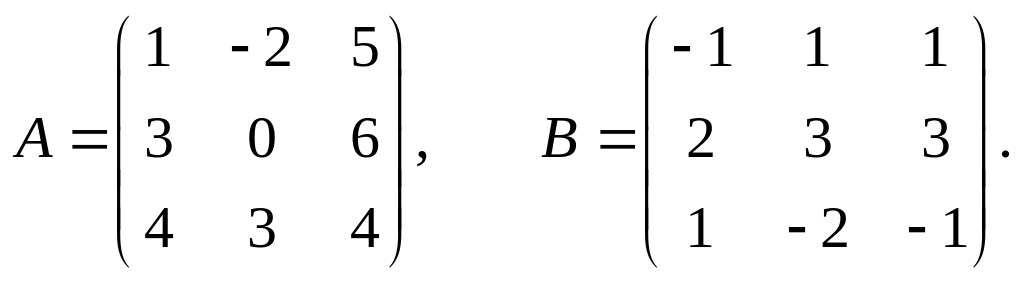
16. 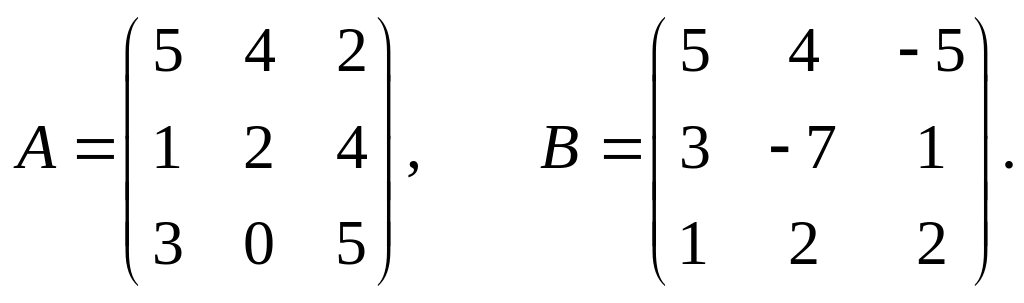
17. 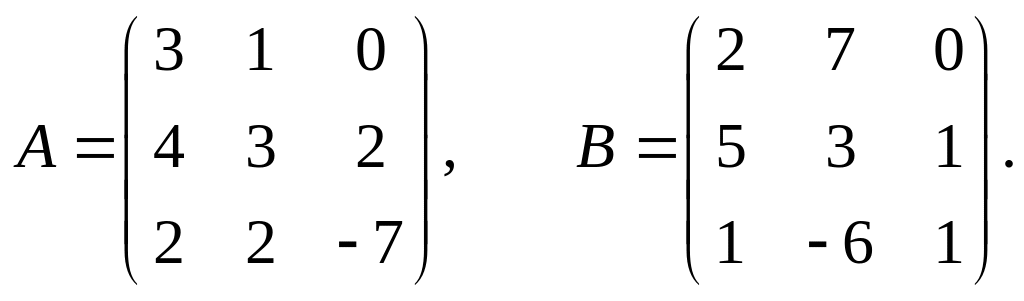
18. 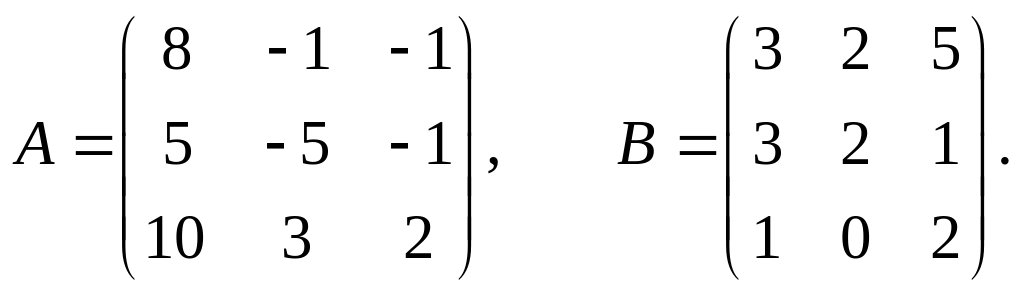
19. 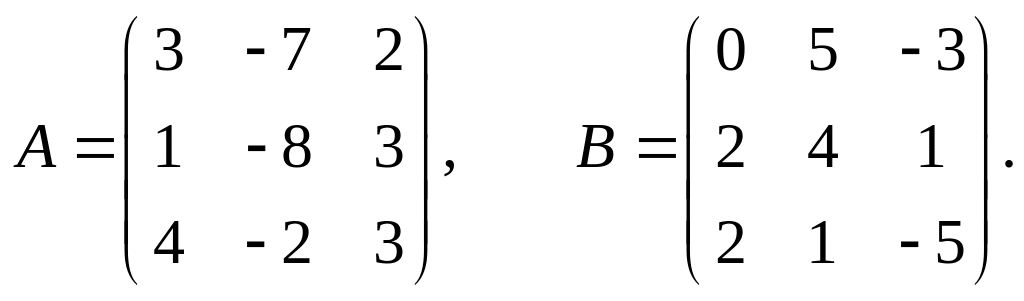
20. 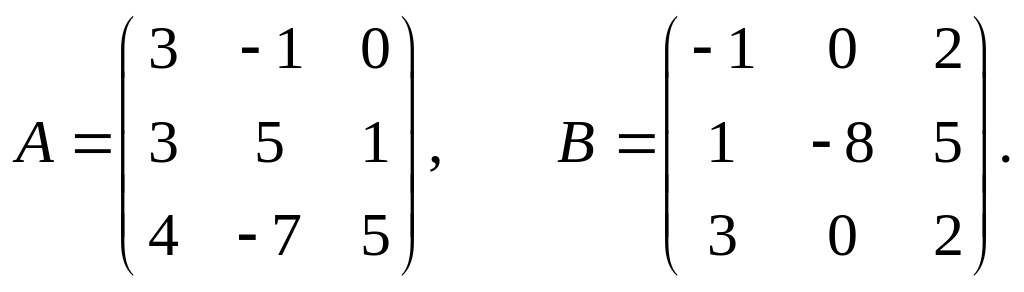
21. 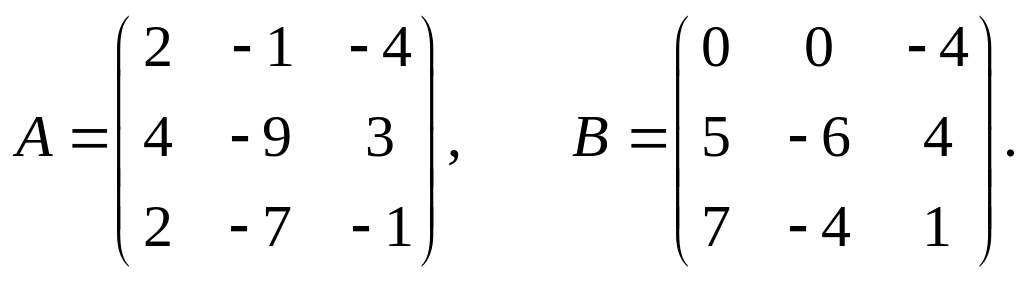
22. 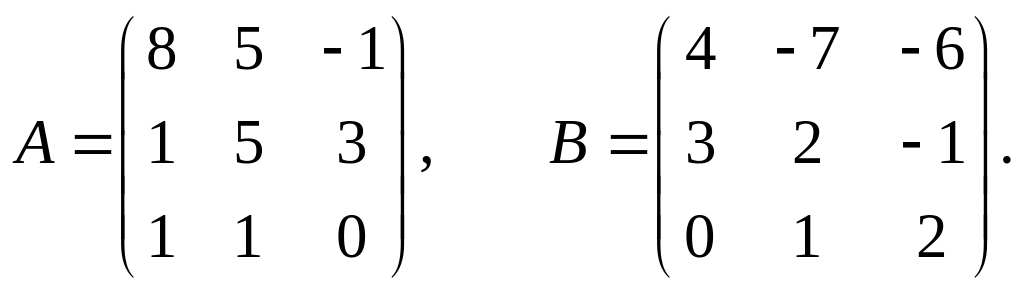
23. 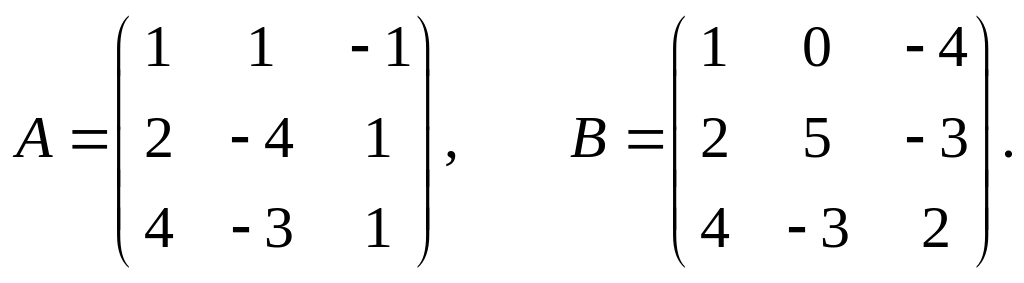
24. 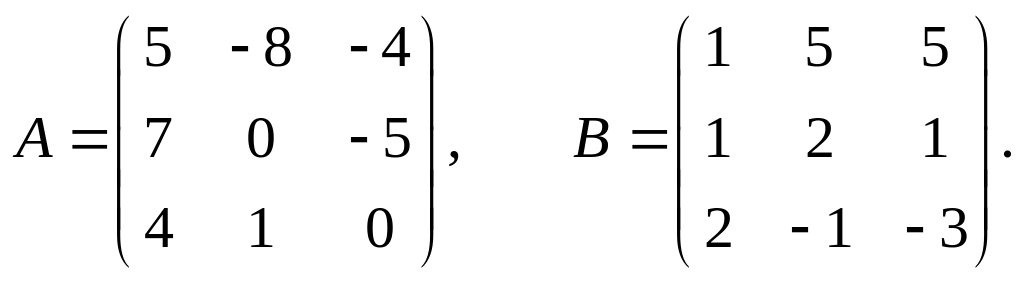
25. 
26. 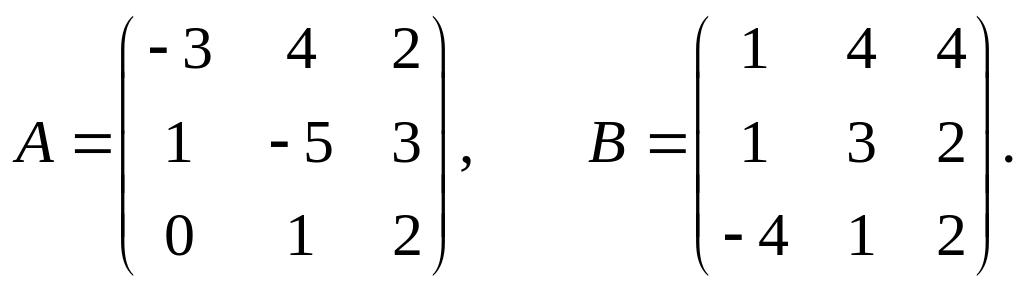
27. 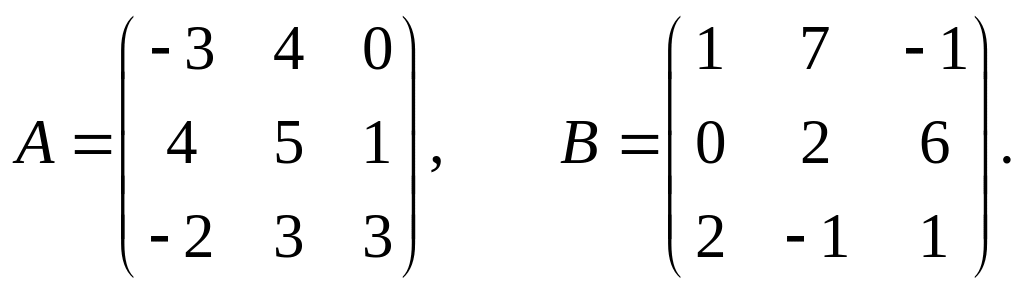
28. 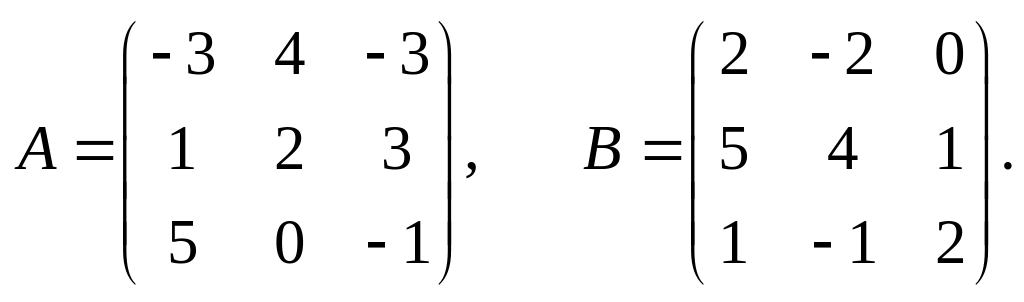
29. 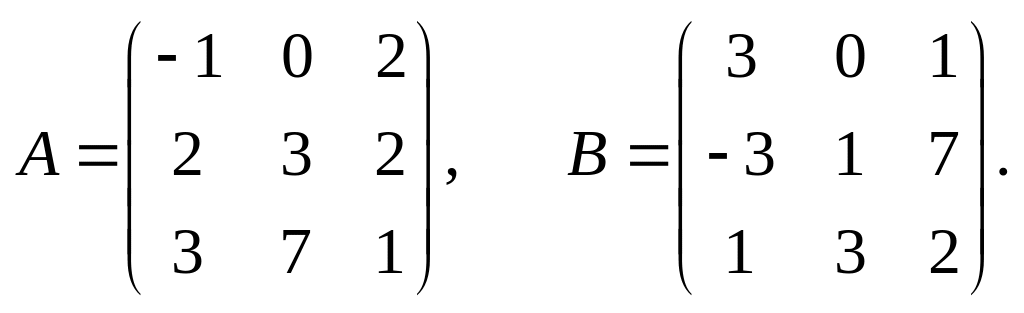
30. 
§3. СИСТЕМЫ ЛИНЕЙНЫХ АЛГЕБРАИЧЕСКИХ УРАВНЕНИЙ
Пример 1.3.
Проверить совместность системы уравнений и в случае совместности решить ее: а) по формулам Крамера; б) с помощью обратной матрицы; в) методом Гаусса.
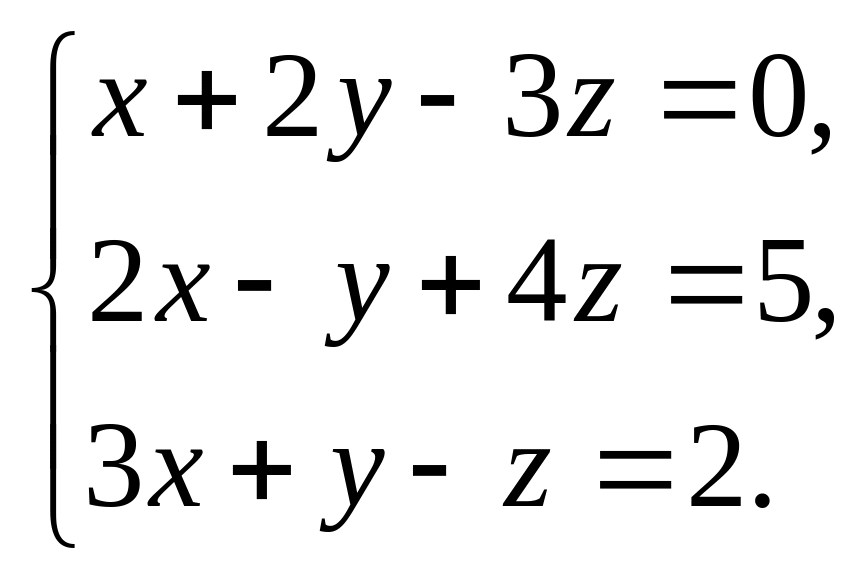
Решение:
Дана система линейных неоднородных алгебраических уравнений. Совместность данной системы проверим по теореме Кронекера-Капелли. С помощью элементарных преобразований найдем ранг матрицы
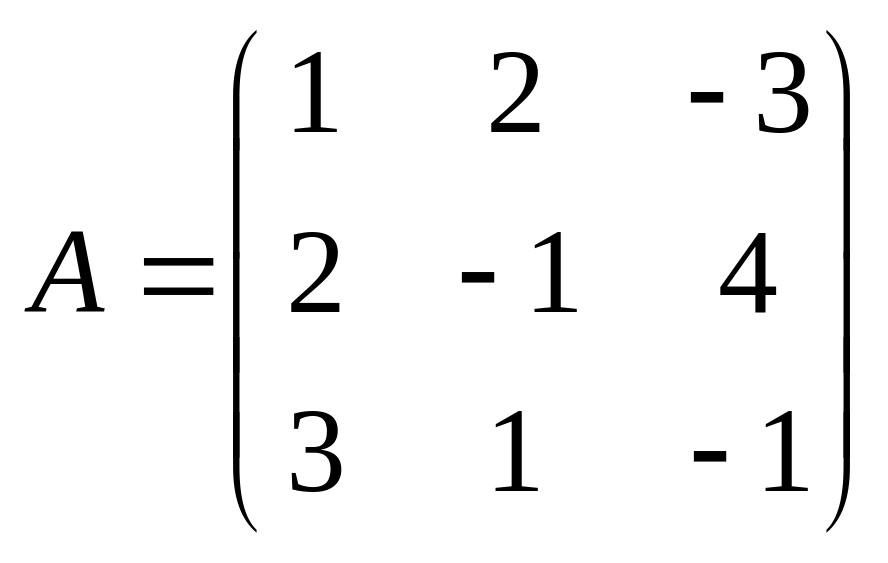
данной системы и ранг расширенной матрицы
 .
.
Для этого умножим первую строку матрицы на (-2) и сложим со второй, затем умножим первую строку на (-3) и сложим с третьей.
Далее из второй строки вычтем третью, в результате в полученной матрице вторую строку сократим на (-5):
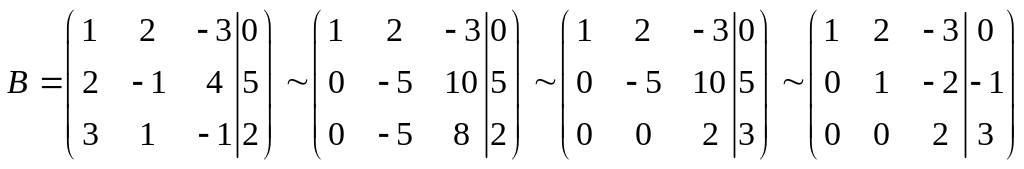
Ранг матрицы в ее
ступенчатом виде равен числу ненулевых
строк. Ранг матрицы
![]() и ранг матрицы
и ранг матрицы
![]() .
.
Так как ранги матриц и одинаковы и равны количеству неизвестных, то данная система совместна и имеет единственное решение.
а) Решим систему линейных уравнений по формулам Крамера.
Вычислим главный определитель системы, составленный из коэффициентов при неизвестных системы:
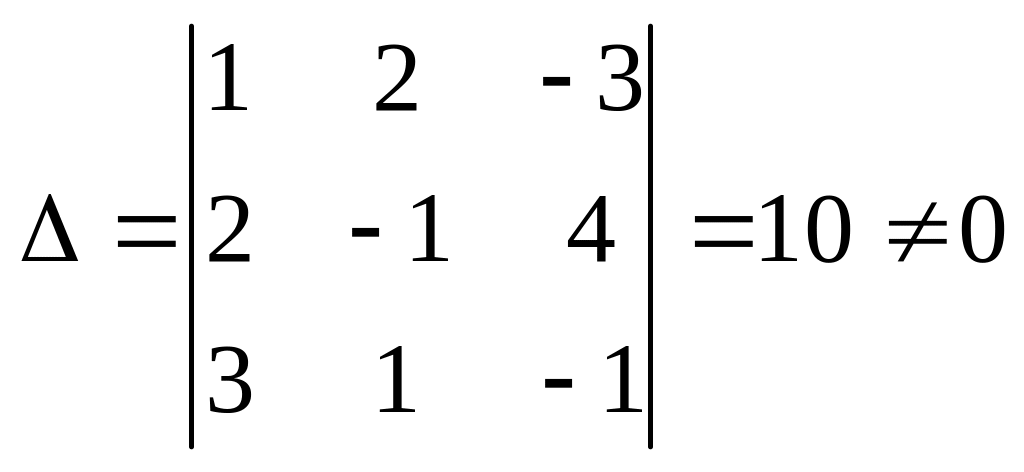 .
.
Так как
![]() ,
то система имеет единственное решение,
которое может быть найдено по формулам
Крамера:
,
то система имеет единственное решение,
которое может быть найдено по формулам
Крамера:
![]() ,
,
где вспомогательные
определители
![]() получаются из главного определителя
путем замены соответственно 1-го, 2-го,
3-го столбцов столбцом свободных членов.
получаются из главного определителя
путем замены соответственно 1-го, 2-го,
3-го столбцов столбцом свободных членов.
Вычислим вспомогательные определители:
 .
.
По формулам Крамера имеем:
![]()
Ответ:
![]() .
.
б) Рассмотрим матричный метод решения данной системы линейных уравнений:
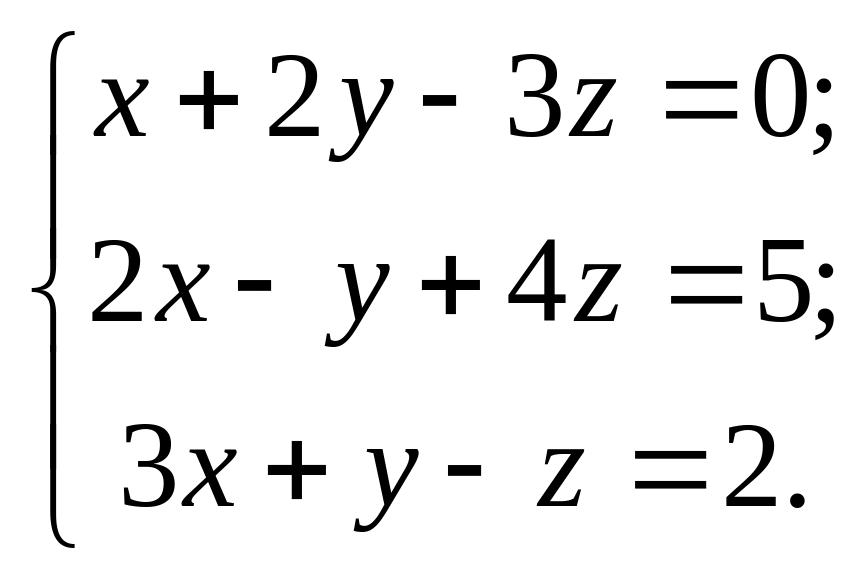
Решение:
Имеем:
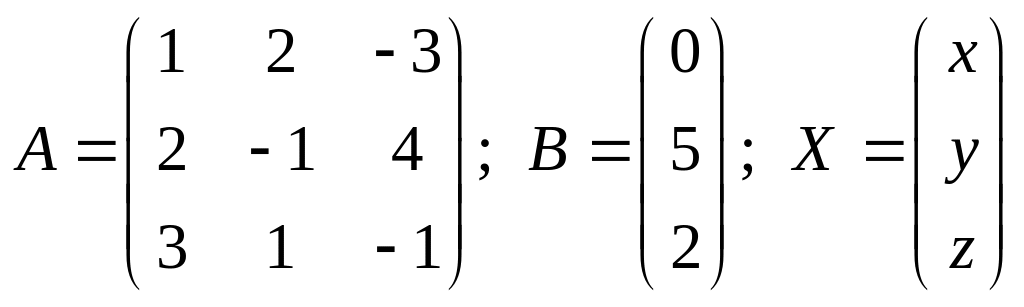
Запишем данную систему в матричной форме:
![]()
Если матрица
- невырожденная, т.е. определитель системы
![]() ,
то, умножая обе части матричного уравнения
,
то, умножая обе части матричного уравнения
![]() на матрицу
слева, получаем решение системы в
матричной форме:
на матрицу
слева, получаем решение системы в
матричной форме:
![]() .
.
Вычислим
![]() (смотри вычисление случай а)).
(смотри вычисление случай а)).
Матрица невырожденная и искомое решение имеет вид:
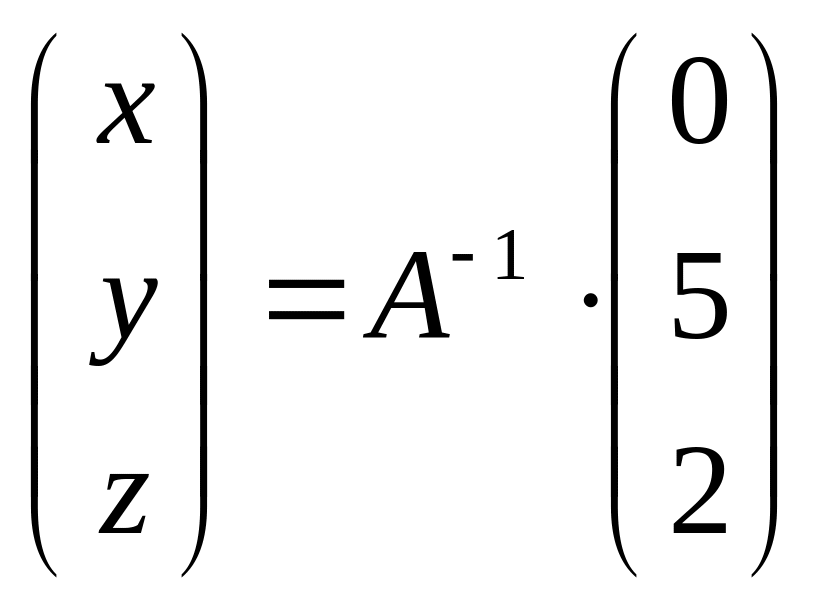 ,
где
- обратная матрица.
,
где
- обратная матрица.
Обратная матрица
существует, т.к.
![]() .
Найдем ее.
.
Найдем ее.
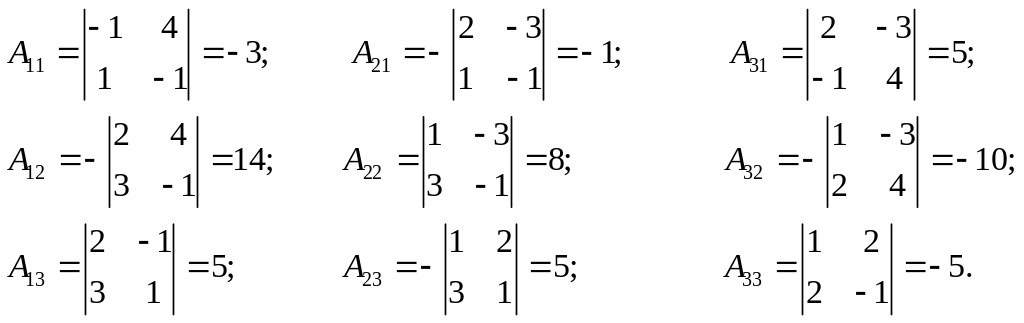
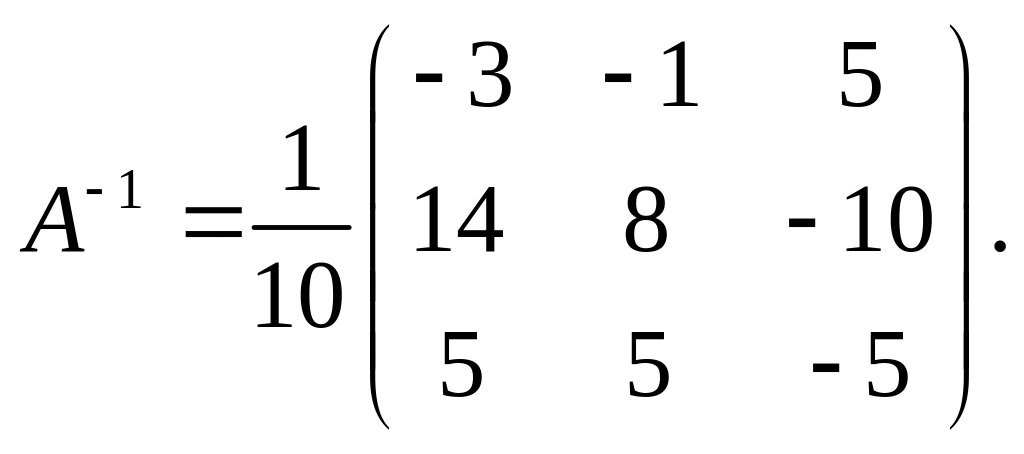
Решение системы:

Ответ:
![]()
в) Решим систему
методом Гаусса. Исключим
![]() из второго и третьего уравнений. Для
этого первое уравнение умножим на (-2) и
сложим со вторым, затем первое уравнение
умножим на (-3) и сложим с третьим
уравнением:
из второго и третьего уравнений. Для
этого первое уравнение умножим на (-2) и
сложим со вторым, затем первое уравнение
умножим на (-3) и сложим с третьим
уравнением:
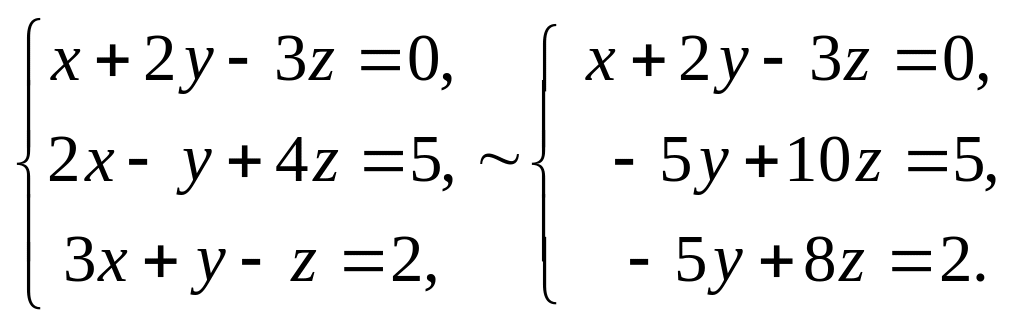
Далее из второго уравнения вычтем третье, и затем все коэффициенты разделим на (-5), получим:
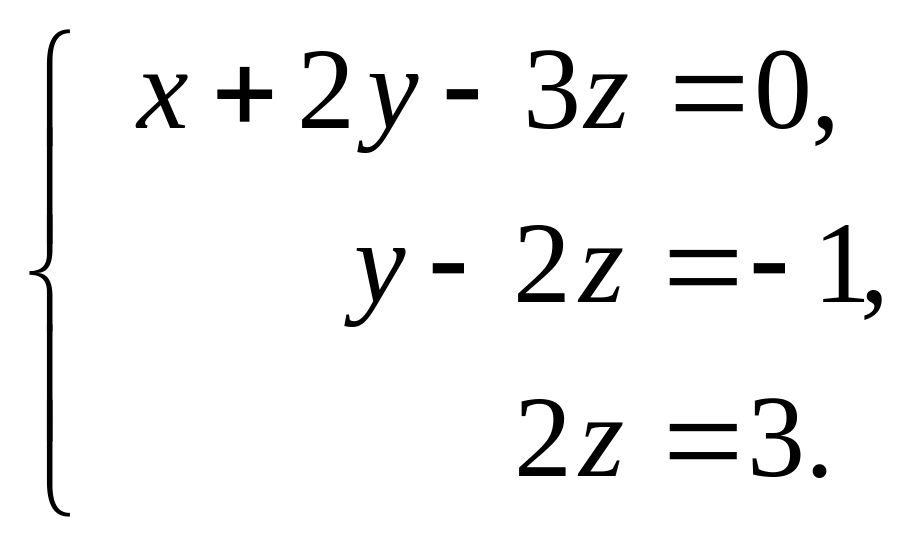
Из полученной системы находим
Ответ:
