
- •Часть 1
- •Введение
- •Глава 1 элементы линейной алгебры §1. Определители Пример 1.1.
- •Пример 1.4.
- •Пример 1.5.
- •Пример 1.6.
- •Пример 2.2
- •Пример 2.3
- •Пример 2.4
- •Пример 2.5
- •Задания для самостоятельного решения. Задание 2.1. Написать разложение вектора по векторам
- •Задание 2.2. Найти косинус угла между векторами и
- •Задание 2.3 Вычислить площадь параллелограмма, построенного на векторах и
- •Задание 2.4. Определить коллинеарны ли векторы и , построенные по векторам и ?
- •Задание 2.5. Вычислить объем тетраэдра с вершинами в точках и его высоту, опущенную из вершины на грань .
- •Глава 3 элементы аналитической геометрии §1. Прямая на плоскости Пример 3.1
- •Задания для самостоятельного решения. Задание 3.1.
- •§2. Плоскость в пространстве Пример 3.2
- •Пример 3.7
- •Пример 3.8
- •Пример 3.10
- •Пример 3.11
- •Пример 3.12
- •Пример 3.13
- •Пример 3.14
- •Глава 4 введение в анализ § 1. Пределы числовых последовательностей Пример 4.1
- •Задания для самостоятельного решения. Задание 4.1 Вычислить пределы числовых последовательностей.
- •§ 2. Пределы функций Пример 4.2 Вычислить пределы дробно-рациональных функций:
- •Пример 4.3
- •Задания для самостоятельного решения. Задание 4.2. Вычислить пределы дробно-рациональных функций
- •Задание 4.3. Вычислить пределы иррациональных функций
- •§ 3. Замечательные пределы. Сравнение бесконечно малых. Пример 4.4
- •Пример 4.5
- •Пример 4.6
- •Задания для самостоятельного решения. Задание 4.4. Вычислить пределы, используя первый замечательный предел и его следствия.
- •Задание 4.5. Вычислить пределы, используя второй замечательный предел и его следствия.
- •Задание 4.6 Определить порядок относительно данной функции, бесконечно малой при .
- •§ 4. Непрерывность функций Пример 4.7
- •Пример 4.8
- •Задания для самостоятельного решения. Задание 4.7. Установить, является ли данная функция непрерывной или разрывной для каждого из данных значений . Сделать схематический чертёж.
- •Пример 5.1
- •Пример 5.2
- •Задание 5.2.
- •Задание 5.3.
- •Задание 5.4.
- •Задание 5.5.
- •Задание 5.6.
- •Задание 5.7.
- •Задание 5.8.
- •Задание 5.9.
- •Задание 5.10.
- •Задание 5.11.
- •Задание 5.12.
- •Задание 5.13.
- •Задание 5.15.
- •Задание 5.16
- •§ 3. Дифференцирование функций, заданных неявно и параметрически Пример 5.17
- •Задание 5.18. Найти и для функций, заданных параметрически.
- •§4. Правило лопиталя Пример 5.19
- •Пример 5.20
- •Задания для самостоятельного решения. Найти указанные пределы, используя правило Лопиталя. Задание 5.19
- •Задание 5.20.
- •§ 5. Полное исследование функций
- •Пример 5.21
- •Пример 5.22
- •Пример 5.23
- •По данным исследования построим график функции .
- •Задания для самостоятельного решения. Провести полное исследование функций и построить их графики Задание 5.21.
- •Задание 5.22.
- •Задание 5.23.
- •§ 6. Применение дифференциала для приближенного вычисления Пример 5.24
- •Пример 5.25
- •Задание 5.25.
- •Литература
- •Содержание
- •Часть 1.
Пример 4.5
Вычислить пределы,
используя второй замечательный предел
и его следствия: а)
![]() ;
б)
;
б)
![]() ;
;
в)
![]() .
.
Решение:
а) .
Второй замечательный
предел:
![]() .
.
В этой задаче
предел основания степени стремится к
1 (разделите числитель и знаменатель на
),
а показатель степени стремится к
бесконечности. Имеем неопределённость
вида
![]() .
Для того, чтобы раскрыть эту неопределённость,
представляем основание степени в виде
.
Для того, чтобы раскрыть эту неопределённость,
представляем основание степени в виде
![]() ,
а в показателе выделяем множитель
,
а в показателе выделяем множитель
![]() ,
где
,
где
![]() - величина бесконечно малая при
- величина бесконечно малая при
![]() .
.
![]()
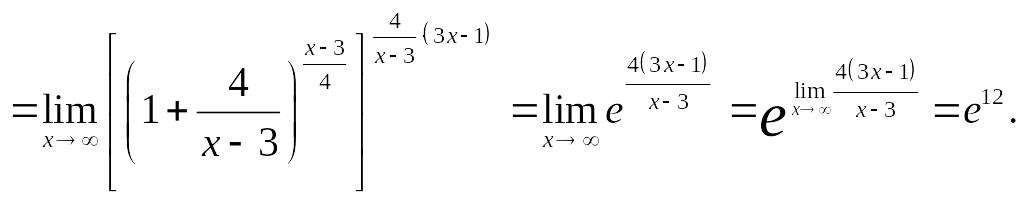
Ответ:
![]() .
.
б) .
Числитель и знаменатель заменим эквивалентными бесконечно малыми функциями:
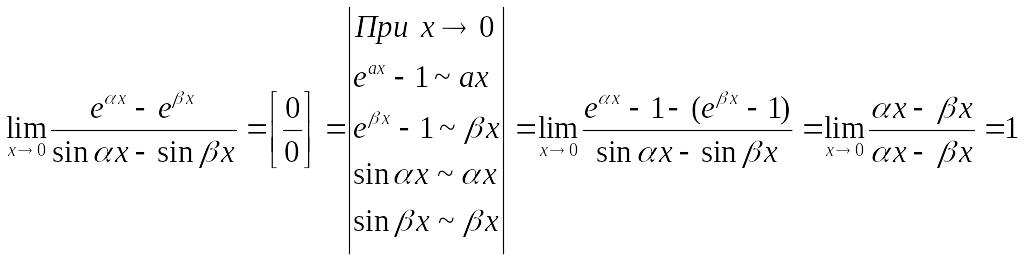
Ответ: 1.
в)
Используя свойства
логарифма, преобразуем выражение
![]() .
Далее, используя второй замечательный
предел, и, учитывая непрерывность функции
.
Далее, используя второй замечательный
предел, и, учитывая непрерывность функции
![]() ,
получим:
,
получим:
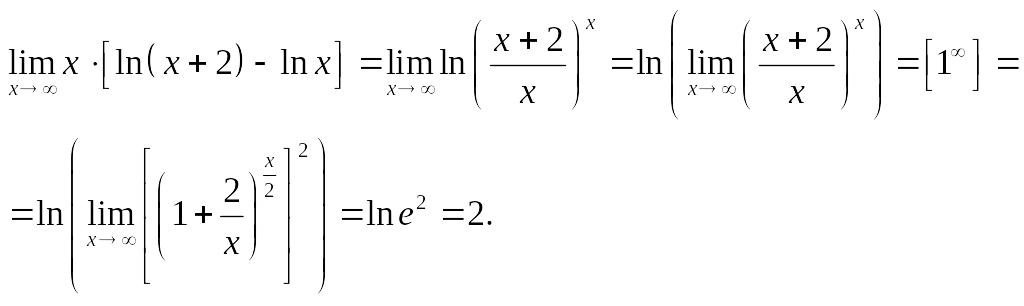 Ответ:
2.
Ответ:
2.
Пример 4.6
Определить порядок относительно функции, бесконечно малой при :
а)
![]() ;
б)
;
б)
![]() ;
в)
;
в)
![]() .
.
Решение:
а) Определить порядок малости относительно функции ?
Будем считать, что
искомый порядок малости равен
,
и определим
так, чтобы
![]() имел конечное значение, отличное от
нуля.
имел конечное значение, отличное от
нуля.
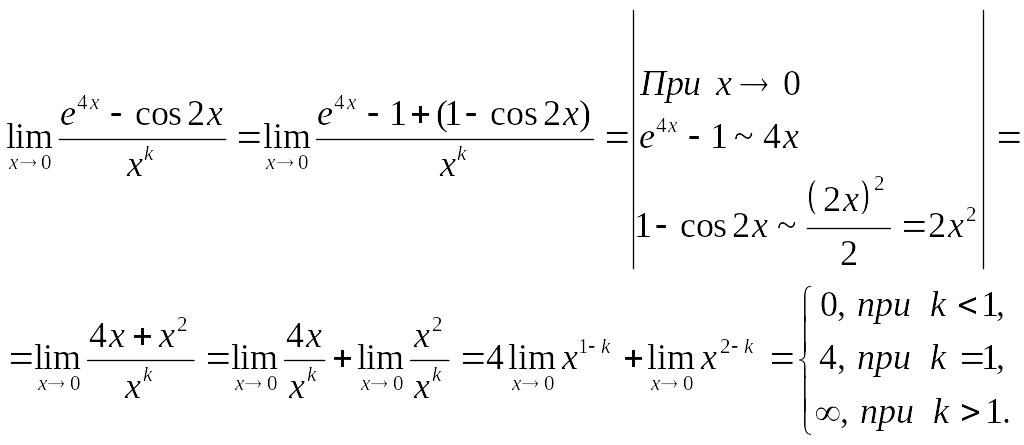
Данная функция
является бесконечно малой одного порядка
![]() при
,
так как при
при
,
так как при
![]() .
.
Ответ: .
б) Определить порядок малости относительно функции ?
Будем считать, что
искомый порядок малости равен
,
и определим
так, чтобы
![]() имел конечное значение, отличное от
нуля.
имел конечное значение, отличное от
нуля.

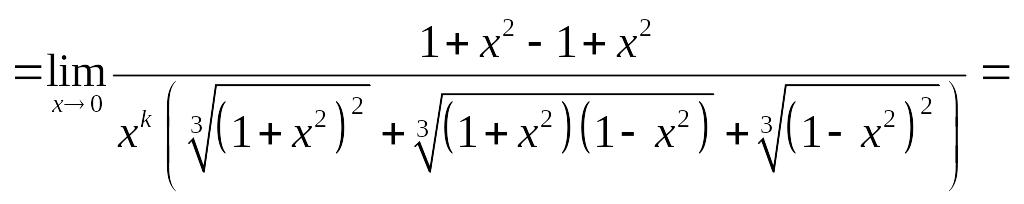
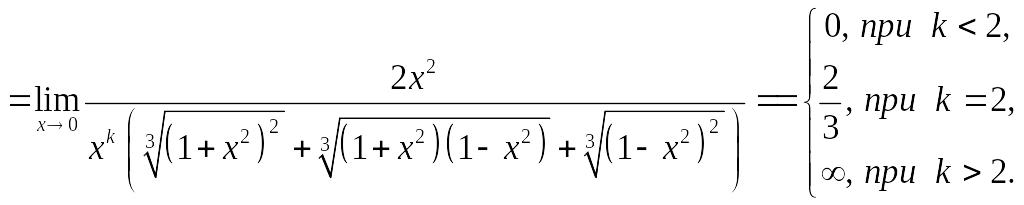
Данная функция
имеет второй порядок малости
![]() относительно бесконечно малой
.
относительно бесконечно малой
.
Ответ:
![]() .
.
в) Определить порядок малости относительно функции ?
Будем считать, что
искомый порядок малости равен
,
и определим
так, чтобы
![]() имел конечное значение, отличное от
нуля.
имел конечное значение, отличное от
нуля.
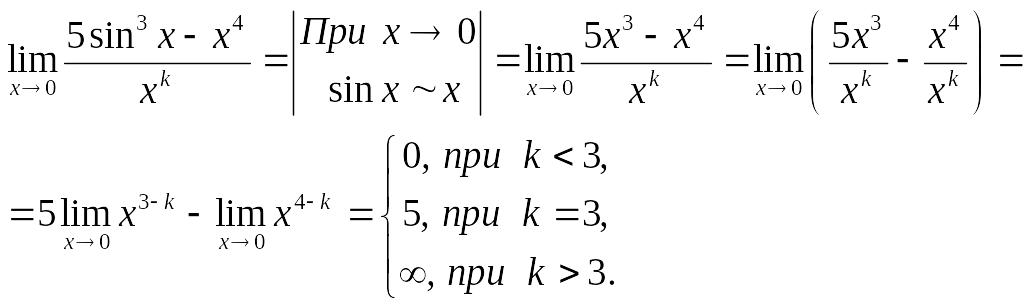
Данная функция
имеет третий порядок малости
![]() относительно бесконечно малой
.
относительно бесконечно малой
.
Ответ:
![]() .
.
Задания для самостоятельного решения. Задание 4.4. Вычислить пределы, используя первый замечательный предел и его следствия.
1. |
|
2. |
|
3. |
|
4. |
|
5. |
|
6. |
|
7. |
|
8. |
|
9. |
|
10. |
|
11. |
|
12. |
|
13. |
|
14. |
|
15. |
|
16. |
|
17. |
|
18. |
|
19. |
|
20. |
|
21. |
|
22. |
|
23. |
|
24. |
|
25. |
|
26. |
. |
27. |
|
28. |
|
29. |
|
30. |
|
Задание 4.5. Вычислить пределы, используя второй замечательный предел и его следствия.
1. |
|
2. |
|
3. |
|
4. |
|
5. |
|
6. |
|
7. |
|
8. |
|
9. |
|
10. |
|
11. |
|
12. |
|
13. |
|
14. |
|
15. |
|
16. |
|
17. |
|
18. |
|
19. |
|
20. |
|
21. |
|
22. |
|
23. |
|
24. |
|
25. |
|
26. |
|
27. |
|
28. |
|
29. |
|
30. |
|

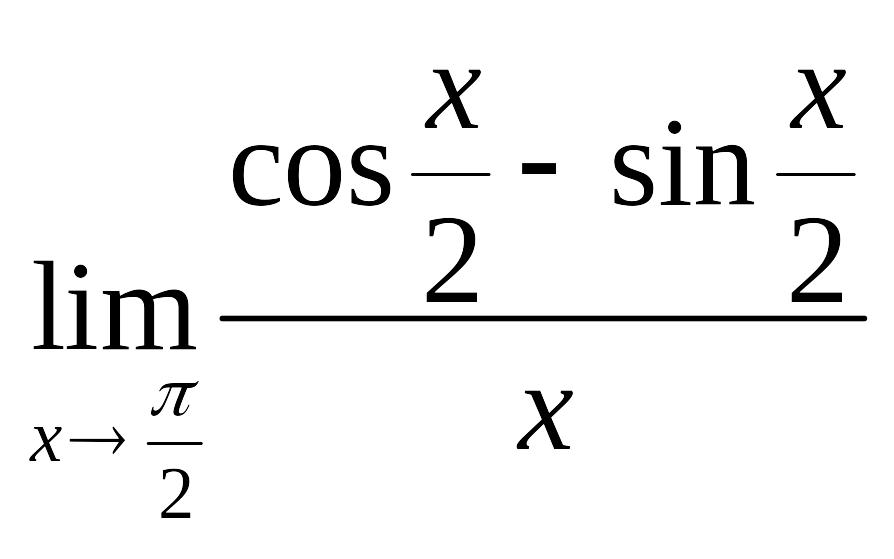 .
.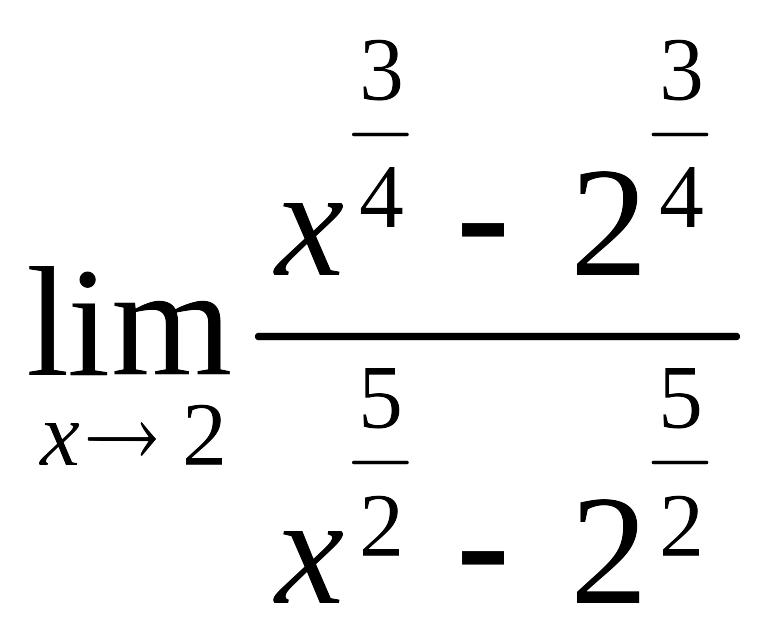 .
.