Глава 4 введение в анализ § 1. Пределы числовых последовательностей Пример 4.1

Вычислить пределы числовых последовательностей:

а) ; б) ;

в) ; г) ;

д) ;

е) .

Решение:

а) .

При числитель и знаменатель дроби стремятся к бесконечности. Имеем неопределенность вида . Для того, чтобы найти предел данной дроби, предварительно преобразуем её, разделив числитель и знаменатель на . Дробь при этом не изменит своей величины, а, следовательно, и своего предела. Далее, учитывая, что пределы последовательностей и равны нулю при , а, также применяя основные теоремы о сходящихся последовательностях, получим:

.

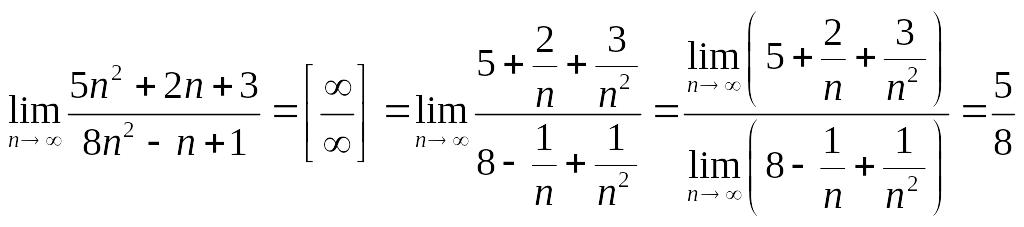Ответ: .

б) .

При числитель и знаменатель дроби стремятся к бесконечности. Чтобы устранить неопределённость , вынесем за скобки в старшей степени. Получим:

.

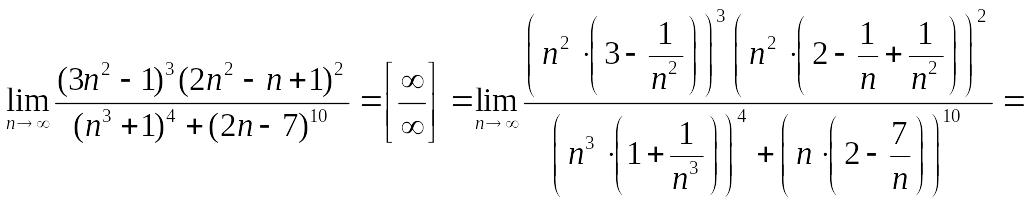
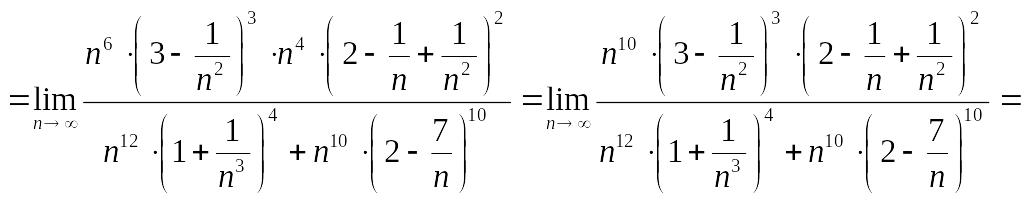
Ответ: 0.

в) .

При числитель и знаменатель дроби стремятся к бесконечности. Чтобы устранить неопределённость , вынесем за скобки в старшей степени. Получим:

=

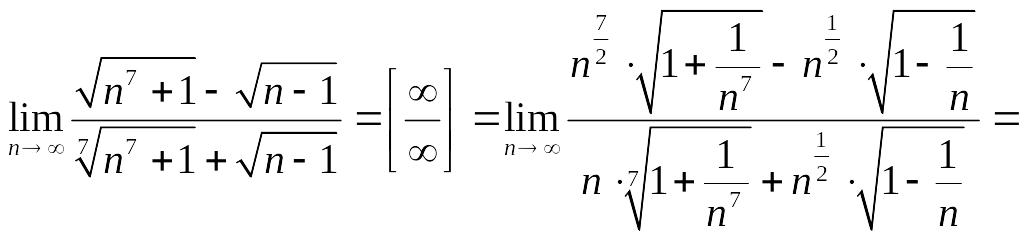
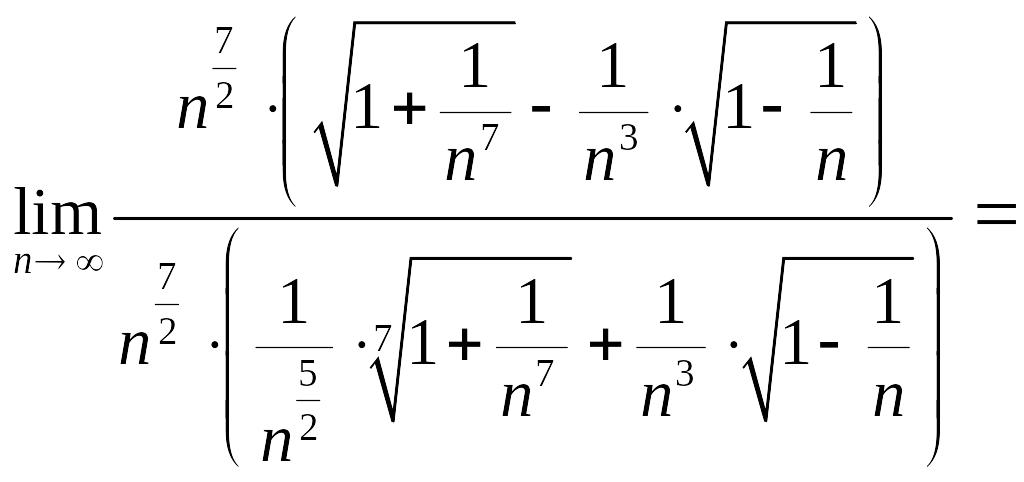
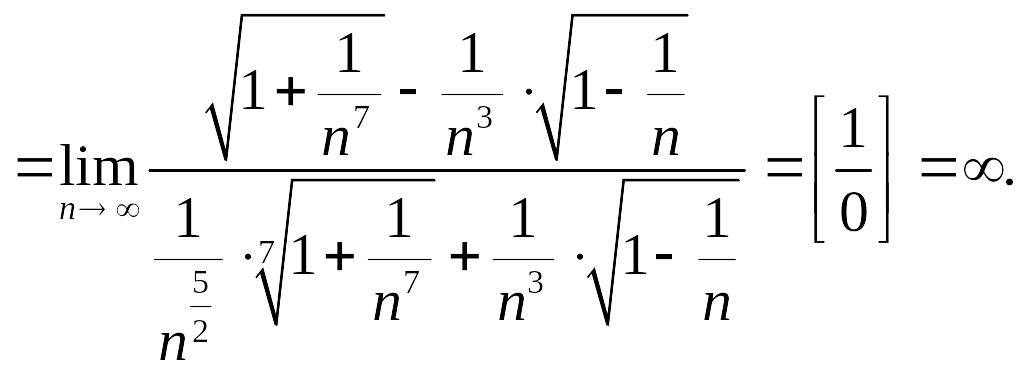
Ответ: .

г) .

По определению . Тогда . Очевидно, что . Выразим и через . Получим:

,

.

Учитывая данные соотношения, после преобразования выражения , приходим к неопределённости , для устранения которой делим числитель и знаменатель на .

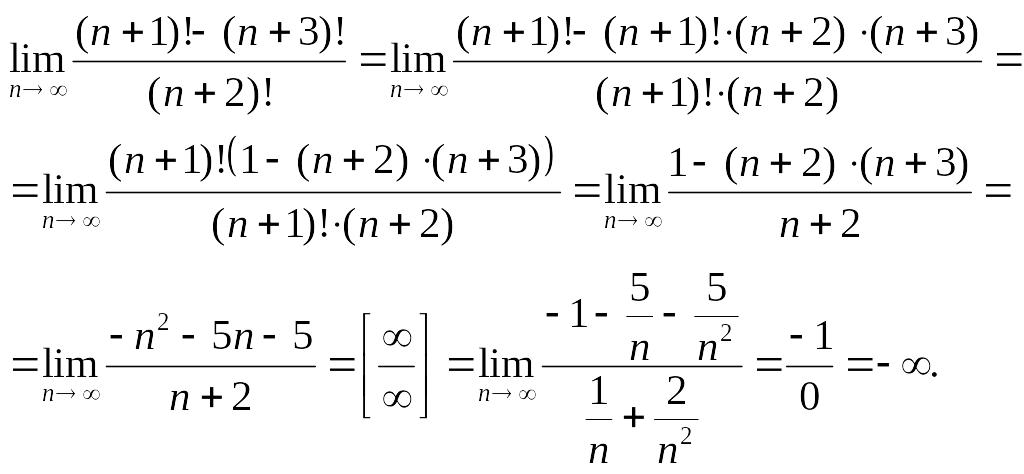
Ответ: .

д) .

В числителе первой дроби записана сумма первых членов арифметической прогрессии. Она равна:

Применяя указанную формулу, а затем, приводя дроби к общему знаменателю, приходим к неопределённости вида . Поделив числитель и знаменатель на , получим:

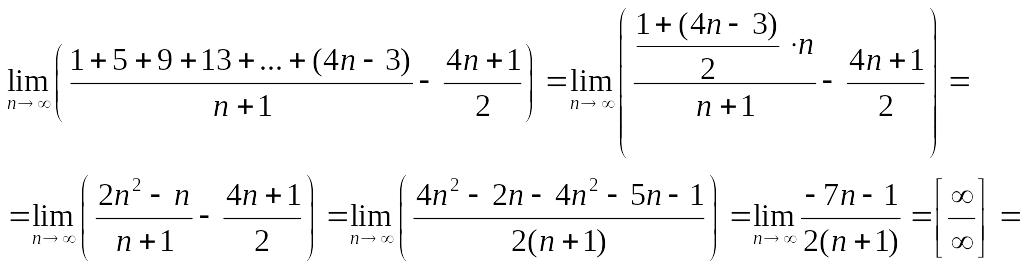
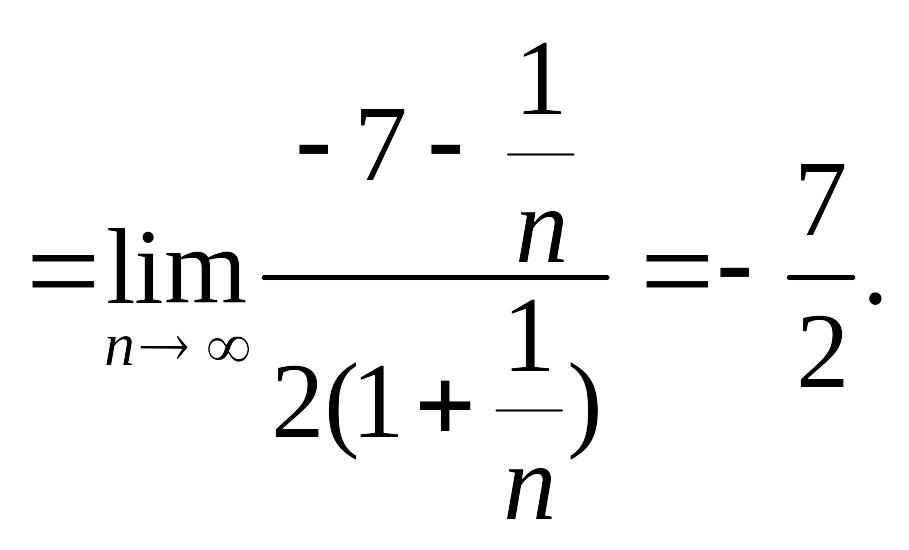
Ответ: .

е) .

Так как

,

а последовательности и представляют собой бесконечно убывающие геометрические прогрессии со знаменателями и соответственно, и сумма бесконечно убывающей геометрической прогрессии , получим:

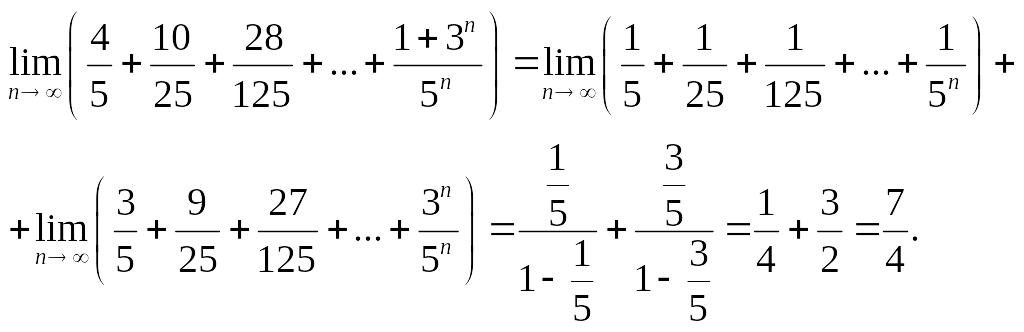
Ответ: .

Задания для самостоятельного решения. Задание 4.1 Вычислить пределы числовых последовательностей.

1.	.	2.
3.	.	4.	.
5.	.	6.	.
7.	.	8.	.
9.		10.	.
11.	.	12.	.
13.	.	14.	.
15.	.	16.	.
17.		18.	.
19.	.	20.	.
21.	.	22.	.
23.	.	24.	.
25.	.	26.	.
27.	.	28.
29.	.	30.

§ 2. Пределы функций Пример 4.2 Вычислить пределы дробно-рациональных функций:

а) ; б) .

Решение:

а) .

Непосредственная подстановка в выражение предельного значения аргумента приводит к неопределенности вида . Следовательно, прежде чем перейти к пределу, необходимо данное выражение преобразовать. Числитель и знаменатель дроби при обращаются в нуль, поэтому многочлены и делятся без остатка на (теорема Безу). Имеем:

;

,

Здесь квадратный трехчлен разложили на множители (если и - корни квадратного уравнения , то ).

В результате получим:

.

Ответ: .

б) .

При подстановке предельного значения аргумента приходим к неопределенности вида . Разложим многочлены и на множители, учитывая, что они без остатка делятся на . Имеем:

0 0

Таким образом, ;

.

Учитывая, что , , получим:

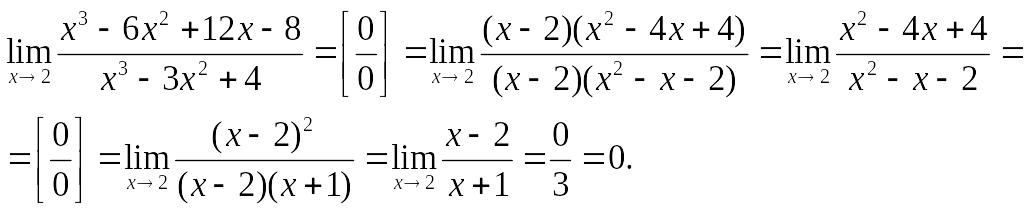Ответ: 0.
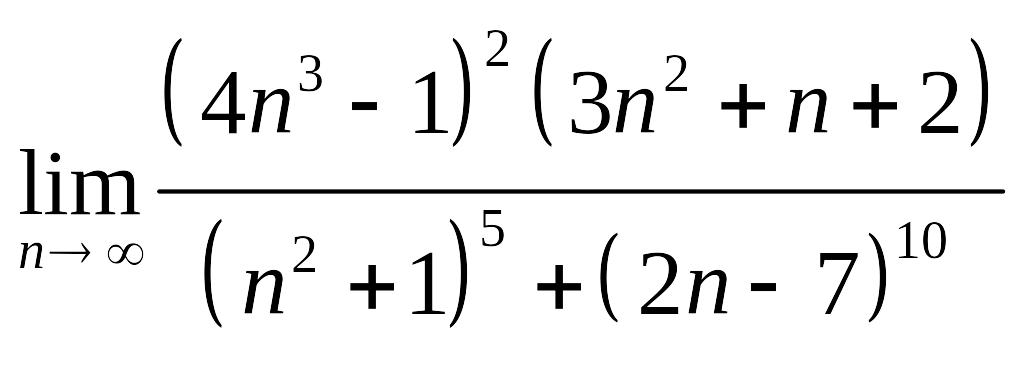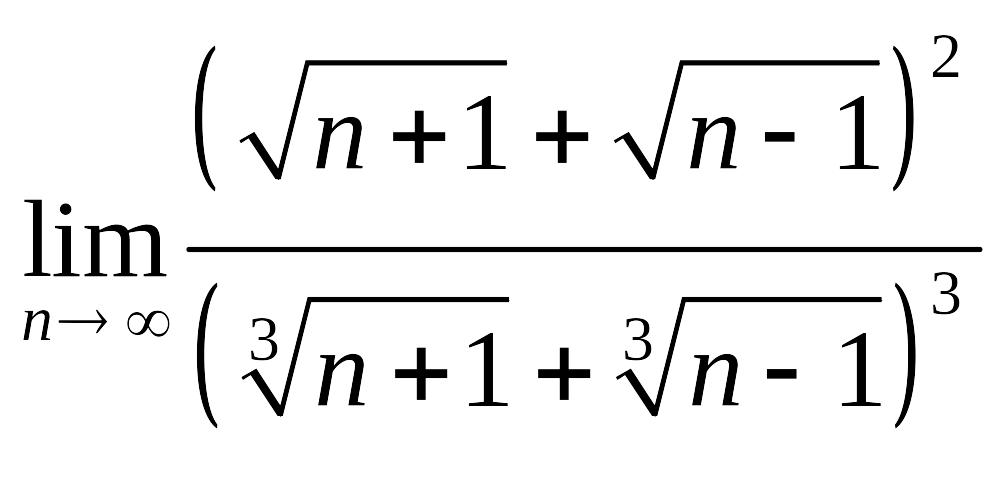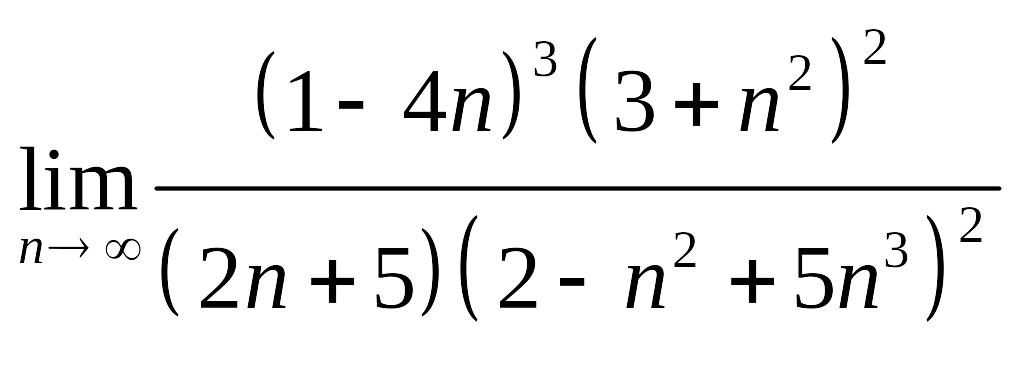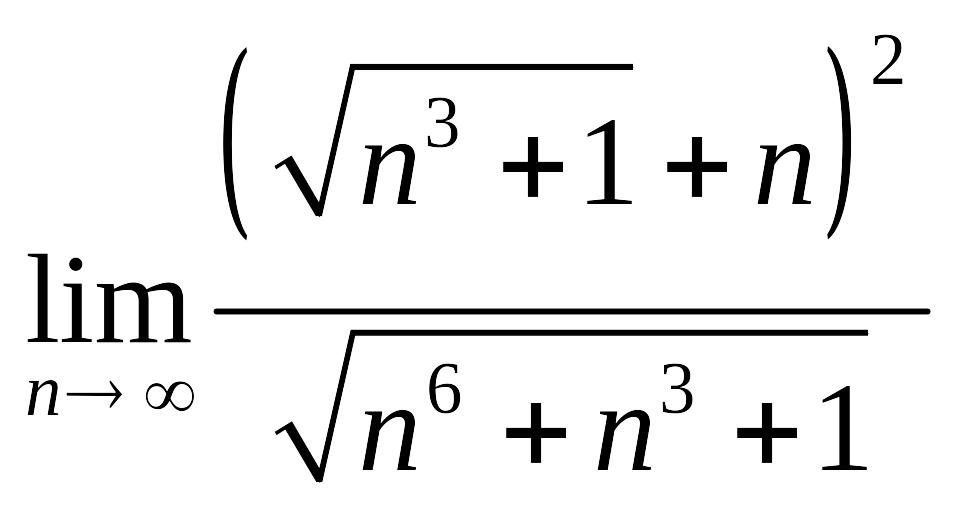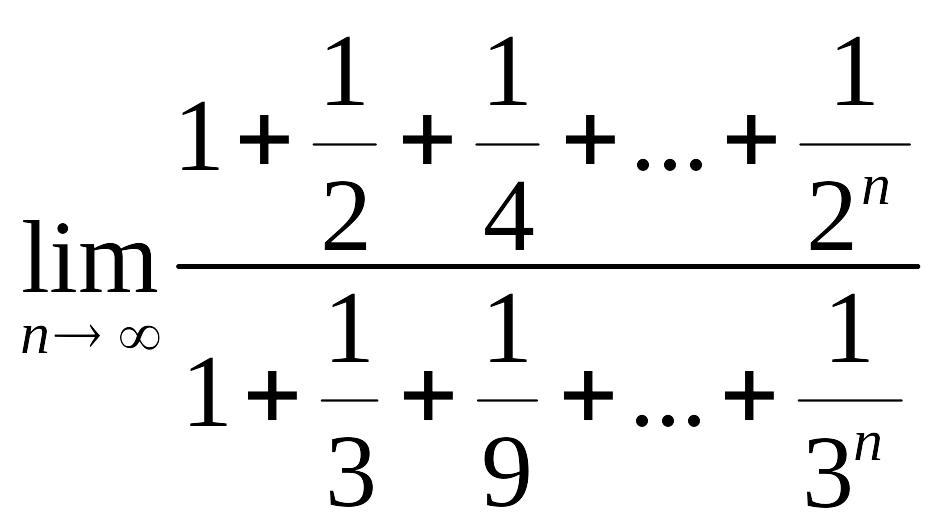