Тема 3. Взаимное расположение прямых в пространстве

22. Через точку С (рис. 42) провести горизонталь h и фронталь f, пересекающие прямую а.

2 2.1. Две прямые пересекаются, если они имеют общую точку [13, 35]. Точка принадлежит прямой, если все ее проекции принадлежат соответствующим проекциям прямой (признак принадлежности точки прямой [34]). Построение фронтали и горизонтали начинаем с той проекции, положение которой относительно осей координат известно (см. задачи 10, 11): для горизонтали – h₂ (параллельна оси Х), для фронтали – f₁ (параллельно оси Х).

22.2. По линиям связи (см. задачу 1 п. 1.3) находим проекции точек пересечения, принадлежащие обеим прямым уровня и прямой а:: точка В для h и точка D для f (рис. 43)

22.3. Соединяем соответствующие проек-ции точек пересечения с проекциями точки С и получаем искомые проекции горизонтали и фронтали.

Рис. 42

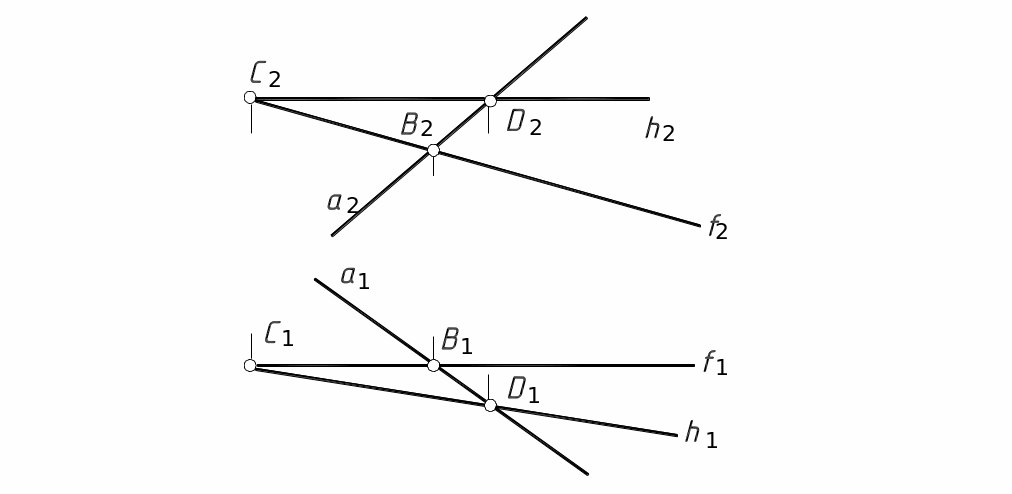
Рис. 43

2 2, а. Через точку С провести горизонталь h, фронталь f и профильную прямую уровня Р, пересекающие прямую а (рис. 44).

Рис. 44

23. Через точку К провести прямую m пересекающую прямые а и b (рис. 45, а).

2 3.1. Прямая m должна иметь общую точку с прямыми а и b. Поэтому начинать построение необходимо с горизонтальной плоскости проекций, т. к. прямая а – горизонтально проецирующая.

23.2. Зная положение т₁ по линиям связи точки 1₁ определяем 1₂ и строим фронтальную проекцию прямой т (рис. 45, б).

а б

Рис. 45

2 3, а. Через точку К провести прямую m, пересекающую прямые а и b (рис. 46)

Рис. 46

2 4. Построить проекции прямой уровня, пересекающей прямые а, b и c и написать её название (рис. 47, а).

а б

Рис. 47

24.1. Задача аналогична задачам 22, 23. Построение необходимо начинать с фронтальной проекции, так как прямая b – фронтально проецирующая прямая (рис. 47, б). Зная свойство прямых уровня показываем фронтальную проекцию горизонтали, пересекающую a, b и c, так как она параллельна оси Х (см. задачу 10).

24.2. Построение горизонтальной проекции аналогично задаче 22. Построенная прямая – горизонтальная прямая уровня h.

24, а. Построить проекции прямой уровня, пересекающей прямые а, b и c и написать её название (рис. 48).

Р ис. 48

2 5. Провести прямую m, пересекающую прямые a, b и с (рис. 49, а).

а б

Рис. 49

25.1. Для построения прямой необходимо знать положение двух точек. В данной задаче, если мы построение начнем с горизонтальной проекции, то может получиться так, что эта прямая пересечет только две прямые, а с третьей будет скрещиваться [14, 36] (не иметь общих точек, так как точки пересечения проекций прямых не лежат на одной линии связи). Поэтому построение необходимо проводить таким образом, чтобы проекция прямой т совпадала с проекцией какой-либо линии, образуя либо параллельные либо пересекающиеся прямые (лежат в одной проецирующей плоскости, см. ниже). Точку пересечения этих прямых определим по второй проекции.

25.2. Для данной задачи практичнее провести фронтальную проекцию прямой т проходящую через проекцию прямой b, а затем определить проекции точек пересечения с прямыми а и с (см. задачи 22, 23).

2 5, а. Провести прямую m, пересекающую прямые a, b и с.

Рис. 50

26. Провести фронталь f, пересекающую m и l, и отрезок АВ (рис. 51, а).

2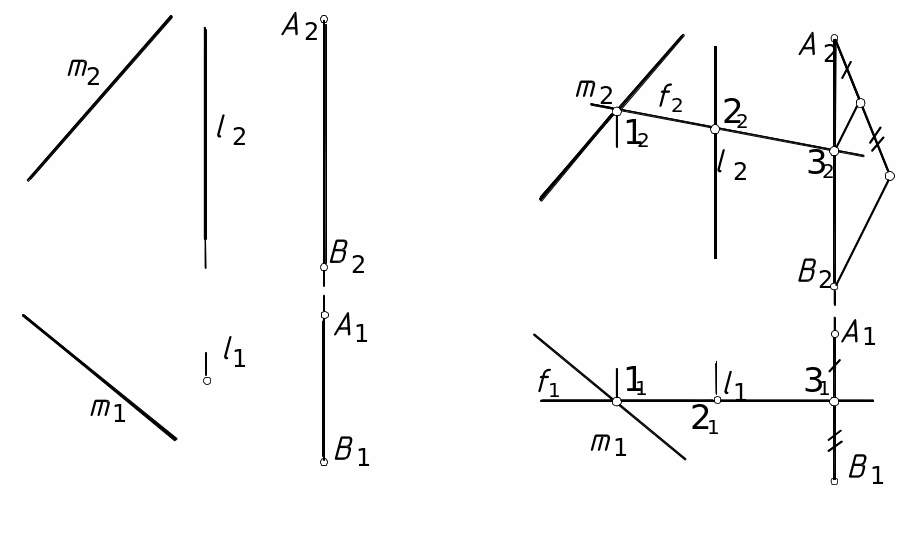 6.1. Строим проекцию фронтали (рис. 51, б), положение горизонтальной проекции которой относительно осей координат известно (см. задачу 10). Находим проекции точек пересечения и по линиям связи (см. п. 1.3) определяем проекции точек пересечения с прямыми m и l. Для определения второй проекции точки пересечения f и АВ необходимо воспользоваться методикой решения задач 15, 18.

а б

Рис. 51

2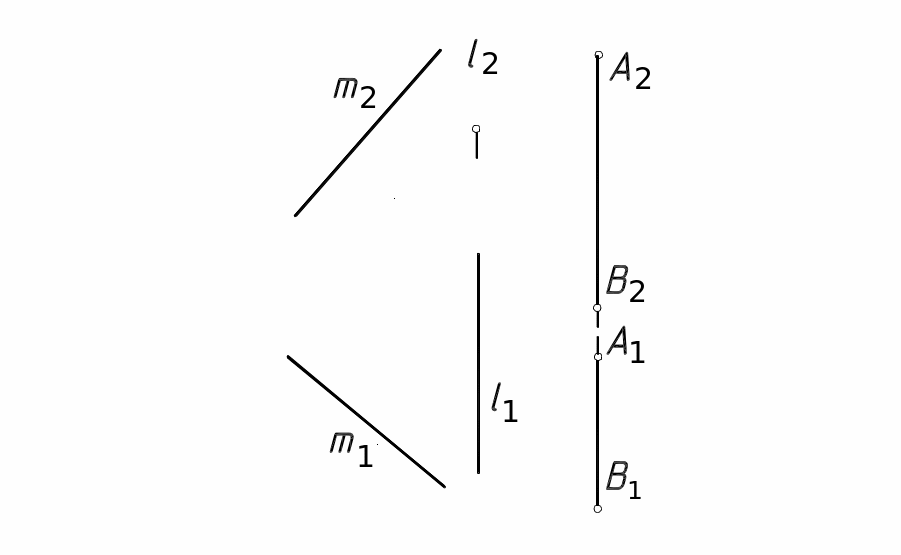 6, а. Провести горизонталь, пересекающую m и l, и отрезок АВ (рис. 52).

Рис. 52

27. Определить расстояние между точкой С и прямой а (рис. 53, а).

27.1. Кратчайшее расстояние между точкой и прямой – перпендикуляр, опущенный из точки на прямую. Угол 90 проецируется в натуральную величину, если одна из его сторон параллельна плоскости проекций, а вторая не перпендикулярна ей (теорема о прямом угле [14]).

2 7.2. Прямая а ‑ горизонталь, так как одна из ее проекций параллельна оси Х (см. свойства горизонтали – задача 10). Поэтому проекция перпендикуляра, опущенного из точки С₁ на а₁ будет соответствовать натуральной величине угла 90.

27.3. Воспользуемся правилом прямоугольного треугольника (задача 9) и определим натуральную величину кратчайшего расстояния от точки С до прямой а – ICBI (рис. 53, б).

а б

Рис. 53

28. Определить расстояние между точкой С и прямой а (рис. 54).

Рис. 54

Контрольные вопросы

1. Перечислите возможные случаи расположения прямых в пространстве. Показать на комплексном чертеже.

2. Сформулируйте признак принадлежности точки прямой.

9. Сформулируйте теорему о прямом угле. Покажите пример на комплексном чертеже.