107

Тема 1. Комплексный чертеж точки

Рис. 1

Решение

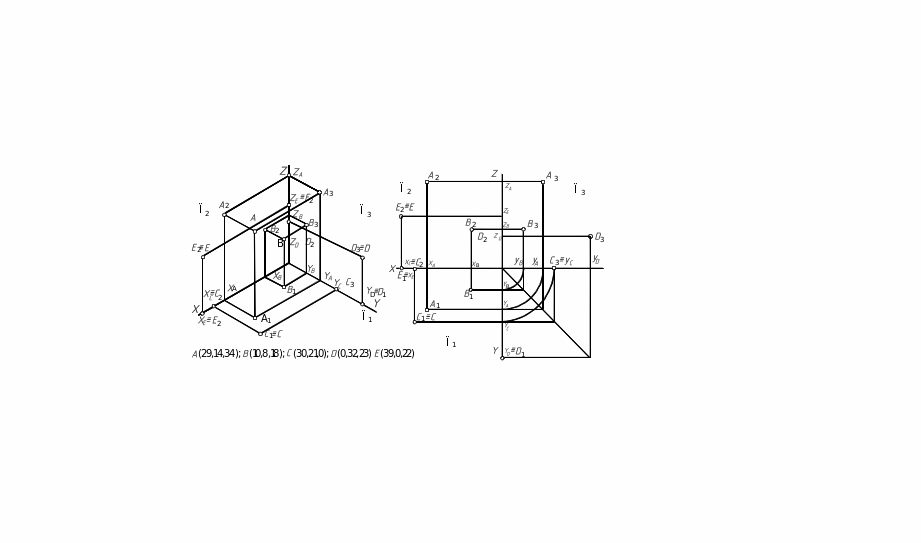
1.1. Ортогональное проецирование [11] – прямоугольная система координат и проецирующие лучи перпендикулярны плоскостям проекций. На наглядном изображении (рис. 2, а) проводим линии, параллельные координатным осям, и находим проекции точек на плоскости проекций. Получаем изображение координат точки: на горизонтальной плоскости проекций П₁ – X и Y; фронтальной плоскости проекций П₂ – Х и Z; профильной плоскости проекций П₃ – Y и Z [18].

1.2. На наглядном изображении показываем координаты точек и при помощи линейки измеряем их значения. Откладываем соответствующие координаты на комплексном чертеже [19] (рис. 2, б). Показываем проекции точки на плоскостях проекций. Обозначаем их.

1.3. Проекции точки должны лежать на одной линии связи [19], соединяющей две проекции и перпендикулярной линии пересечения соответствующих плоскостей проекций (оси X, Y, Z и т. д.), рис. 1, а. По наглядному изображению точек (рис. 3) определить их координаты, показать недостающие проекции и построить комплексный чертеж в трех проекциях. Обозначить плоскости проекций и написать их название.

а б

Рис. 2

1 , а. По наглядному изображению точек определить их координаты, показать третью проекцию и построить комплексный чертеж в трех проекциях (рис. 3). Обозначить плоскости проекций и написать их название.

А( ); B( ); C( ); D( ); E( ); F( );

G( ); H( )

Рис. 3

2. По комплексному чертежу задачи 1 (рис. 2) определить положение точек относительно точки А.

Решение

2.1. Точка находится правее [21], если ее координата X (см. задачу 1) меньше. Определяем по горизонтальной или фронтальной плоскости проекций – правая точка располагается правее. Таким образом для нашего случая точками находящимися правее точки А, будут: B, D; левее Е и F.

2.2. Точка находится выше [21], если ее координата Z (см. задачу 1) больше. На фронтальной и профильной плоскостях проекций точка располагается выше. Выше точки А, для задачи, точек не будут. Остальные точки расположены ниже.

2.3. Точка находится ближе [21] к наблюдателю, если ее координата Y (см. задачу 1) больше. На горизонтальной плоскости проекций находится ниже, а на профильной плоскости проекций правее, и для нашего случая: ближе точки А – точки С и D; остальные – В и Е – дальше.

2, а. При условии задачи 2 решить задачу (рис. 3).

Правее: Левее:

Выше: Ниже:

Ближе: Дальше:

3. Даны точки: А(30, 20, 10), В(40 -25, 50), С(10, 50, 0), D(0, 0, 0). Определить (по значениям координат) правую, левую, высшую, низшую, ближайшую и наиболее удаленную точки.

Решение:

Правая – D, так как ее координата Х наименьшая.

Левая – B, так как ее координата Х наибольшая.

Высшая – B, так как ее координата Х наибольшая.

Низшие – C, D, так как их координата Z наименьшая.

Ближайшая – C, так как ее координата Х наибольшая.

Наиболее удаленная – B, так как ее координата У наименьшая.

3, а. Даны точки: А(-30, 20, 10), В(40 -25, -50), С(10, -50, 0), D(0, 0, 0). Определить (по значениям координат) правую, левую, высшую, низшую, ближайшую и наиболее удаленную точки.

Правая – Высшая ‑ Ближайшая –

Левая – Низшая ‑ Наиболее удаленная –

4 . По комплексному чертежу определить положение точки A относительно точки В (рис. 4, а) и С относительно D (рис. 4, б).

а б

Рис. 4

5. Построить наглядные изображения и эпюр точек задачи № 3, а и проверить правильность нахождения положения точек друг относительно друга.

Решение

5.1. Решение аналогично задачи 1. По известным координатам показываем наглядное изображение точек и строим их эпюр (рис. 5). Координата Y точки В отрицательна, поэтому (на эпюр) она совпадет с положительными координатами осей Z и X, но не будет им равна.

Р ис. 5

5, а. Построить наглядные изображения и эпюр точек задачи № 3, а и проверить правильность решения (рис. 6).

Р ис. 6

6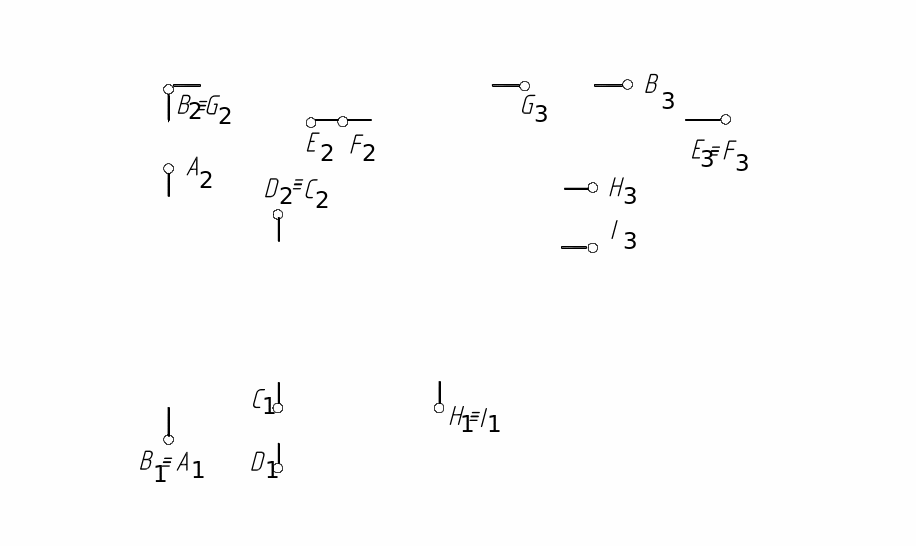 . Определить видимость точек, изображенных на чертеже. Написать их названия (рис. 7).

Рис. 7

Решение

6.1. Точки, у которых одна из проекций совпадает (одинаковая координата), называются конкурирующими [23]. Плоскость, на которой проекции совпадают, определяет название этих точек (горизонтально, вертикально и профильно конкурирующие точки). На другой плоскости проекций эти точки лежат на одной линии связи.

6 .2. Видимость [23] точек (рис. 8) определяем по направлению проецирования (взгляда, направленного в сторону, противоположную положительного отсчета координат (стрелка): – для горизонтально-конкурирующих точек направление проецирования сверху вниз на фронтальной и профильной плоскостях проекций, фронтально-проецирующих точек – снизу вверх на горизонтальной плоскости проекций и справа налево на профильной плоскости проекций, профильно-конкурирующих – слева направо на горизонтальной и фронтальной плоскости проекций.

6.3. При символьном обозначении видимости сначала пишется видимая точка, а затем в круглых скобках – невидимая, например А₁(В₁) – горизонтально-конкурирующие точки, из которых точка А видна. Для нашего случая имеем (рис. 8):

B(G) – фронтально-конкурирующие;

В(А) – горизонтально-конкурирующие;

H(I) – горизонтально-конкурирующие;

Е(F) – профильно-конкурирующие;

D (C) – фронтально-конкурирующие.

Рис. 8

6, а. Определить видимость точек, изображенных на чертеже (рис. 9). Написать их названия.

Р ис. 9

7. По двум проекциям точки А построить третью (рис. 10, а).

Решение

7 .1. Построение третьей проекции точки по двум известным [27] основано на том, что любые две проекции точки определяются тремя координатами, две из которых определяют положение какой-либо проекции. Так для нашего случая, чтобы определить положение третьей проекции (рис. 10, б), достаточно определить координату Y_A на горизонтальной проекции и отложить ее вдоль линии связи А₂–А_3.

а б)

Рис. 10

7, а. По двум проекциям точек построить третью (рис. 1.11).

7 .1. Рассмотреть пару точек, имеющих одноименные проекции, для которых произвольно показать систему координат (удобнее начало координат совместить с одной из точек. Далее см. задачу 7.

Рис. 11

Контрольные вопросы

1. Ортогональное проецирование точки.

2. Основные плоскости проекций (наименование и их расположение в пространстве).

3. Проекции точки на три основные и дополнительные плоскости проекций (наглядное представление и комплексный чертеж).

4. Линии связи, их расположение по отношению к линии пересечения плоскостей проекций (координатным осям).

5. Определение по комплексному чертежу и координатам взаимного расположения точек в пространстве (правее, левее; выше, ниже; ближе, дальше).

7. Конкурирующие точки, определение видимости точек.

8. Построение третьей проекции точки по двум известным.