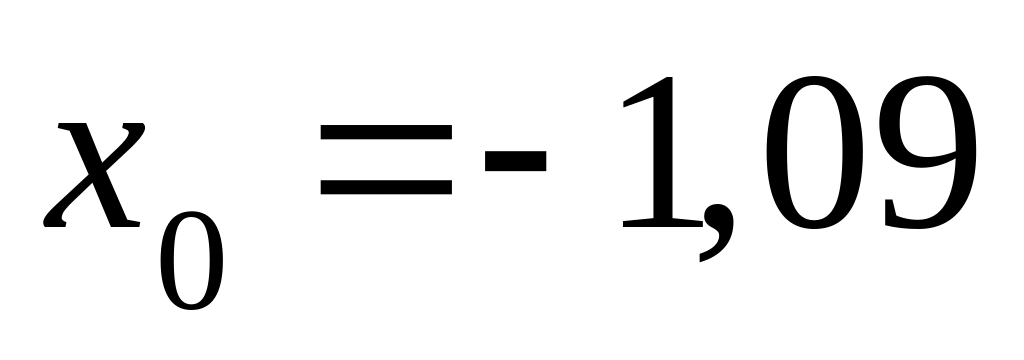- •Лабораторная работа № I приближенное решение уравнений
- •1.1. Общие сведения
- •1.2. Отрезки изоляции корней
- •1.3. Метод половинного делении
- •1.4. Комбинированный метод хорд и касательных
- •Пример 3. Решить уравнение методом хорд и касательных с точностью 0,01, если известен отрезок изоляции корня .
- •1.5. Сравнительная характеристика методов
- •1.6. Метод итераций.
- •Задания
1.4. Комбинированный метод хорд и касательных
Комбинированный метод включает в себя одновременное применений двух независимых методов приближенного решения уравнений: метода касательных (метод Ньютона) и метода хорд, каждый из которых дает алгоритм построения приближающих последовательностей, сужающих отрезок изоляции корня.
В методе хорд за приближенное значение корня принимаем абсциссу точки пересечения хорды АВ с осью Ох (см. рис. 1.5), при этом
![]() , (1.5)
, (1.5)
а отрезок изоляции корня
(в данном случае) сужается в
![]() .
При других вариантах расположения
графика функции отрезок изоляции корня
может быть другим (а именно,
.
При других вариантах расположения
графика функции отрезок изоляции корня
может быть другим (а именно,
![]() ).
).
В методе касательных за приближенное значение корня принимаем абсциссу точки пересечения касательной, проведенной к графику функции в точке В с осью Ох (см. рис. 1.6), при этом
![]() , (1.6)
, (1.6)
а отрезок изоляции корня
(в данном случае) сужается в
.
При других вариантах расположения
графика функции касательную следует
проводить в точке А,
при этом
![]() ,
а отрезок изоляции корня может быть
.
Вообще, касательную
проводят в том конце отрезка изоляции
корня, где значение функции и ее второй
производной имеют одинаковые знаки (
,
а отрезок изоляции корня может быть
.
Вообще, касательную
проводят в том конце отрезка изоляции
корня, где значение функции и ее второй
производной имеют одинаковые знаки (![]() ,
где с
– это либо a,
либо b).
,
где с
– это либо a,
либо b).
Смысл одновременного применения обоих методов виден на рис. 1.7. При этом отрезок изоляции корня сужается с обеих сторон, что гарантирует высокую эффективность метода.
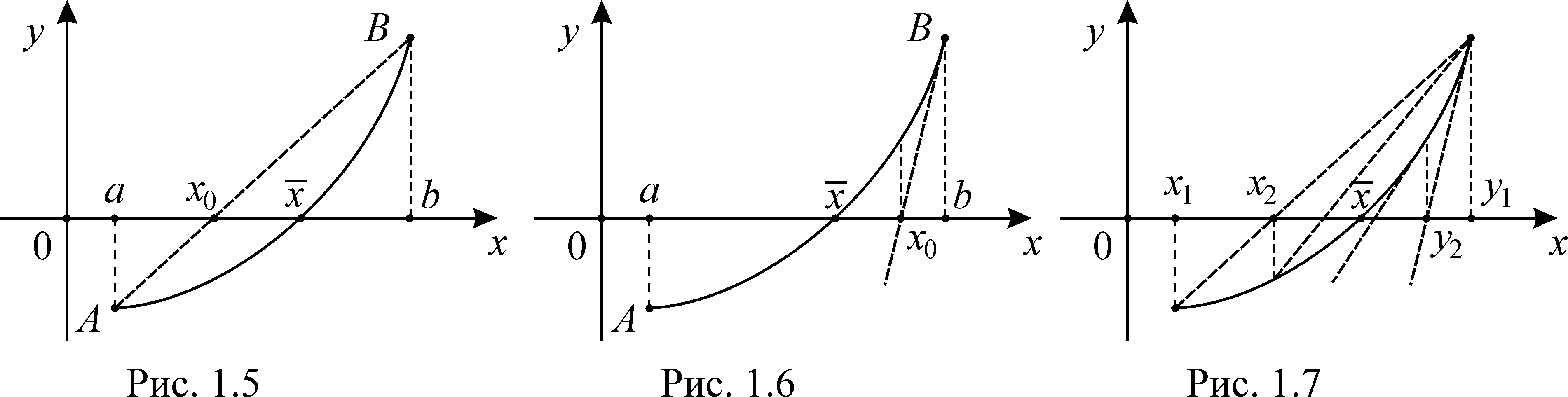
При этом, если – приближающая последовательность, построенная по методу хорд, a – по методу касательных, то одна из них будет монотонно возрастающей, а вторая – монотонно yбывающей. При других вариантах расположения графика функции последовательности могут меняться местами.
Точный алгоритм построения этих последовательностей следующий:
1) находим отрезок изоляции корня и проверяем условия применимости комбинированного метода:
а) непрерывность
,
![]() и
и
![]() на
;
на
;
б) ;
в) и не обращаются в нуль на .
2) задаем начальные приближения (![]() - начальное приближение для метода хорд,
- начальное приближение для метода хорд,
![]() - начальное приближение для метода
касательных):
- начальное приближение для метода
касательных):
а) если выполнено условие
![]() ,
то
,
;
,
то
,
;
б) в противном случае
![]() ,
,
![]() .
.
3) по формулам (1.5) и (1.6) находим другие
элементы приближающих последовательностей.
А именно:
![]() ,
,
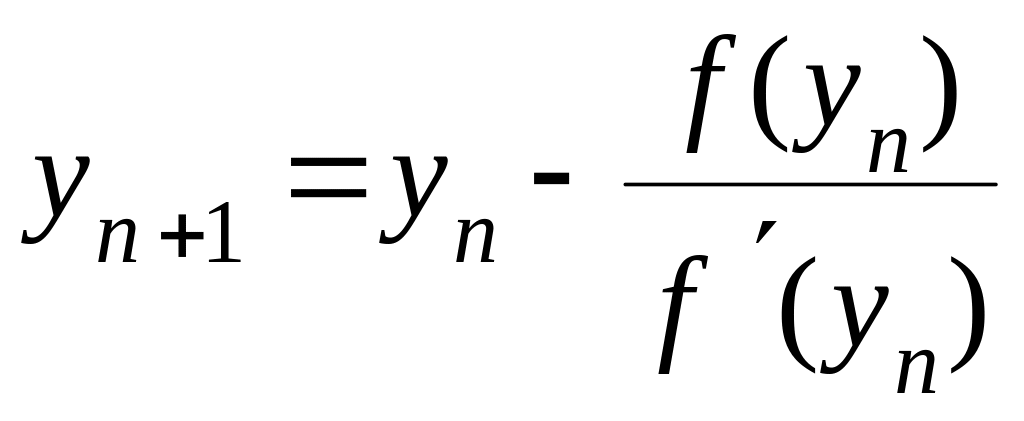 .
.
Остановка вычислений производится при выполнении условия (1.2), приближенное значение корня определяется по формуле(1.3).
Достоинство метода: быстрое получение результата при заданной точности.
Недостаток метода: относительная сложность при проверке всех необходимых для применения метода условий.
Упражнение 6. Докажите: если , то последовательность будет монотонно убывающей, а – монотонно возрастающей.
Упражнение 7.
Докажите: если
![]() ,
то последовательность
будет монотонно убывающей, а
– монотонно возрастающей.
,
то последовательность
будет монотонно убывающей, а
– монотонно возрастающей.
Упражнение 8. Сделайте иллюстрации комбинированного метода для случаев:
1)
![]() ,
,
![]() на
;
на
;
2)
,
![]() на
;
на
;
3)
![]() ,
на
.
,
на
.
Упражнение 9. Почему комбинированный метод нельзя использовать в случаях, указанных на рис. 1.2 и 1.3?
Пример 3. Решить уравнение методом хорд и касательных с точностью 0,01, если известен отрезок изоляции корня .
Решение.
Как мы
знаем из примера 2, это уравнение имеет
только один корень, и он находится на
отрезке
.
Вычислим значения функции
на концах отрезка:
![]() ,
,
![]() .
.
Проверим выполнение условия б):
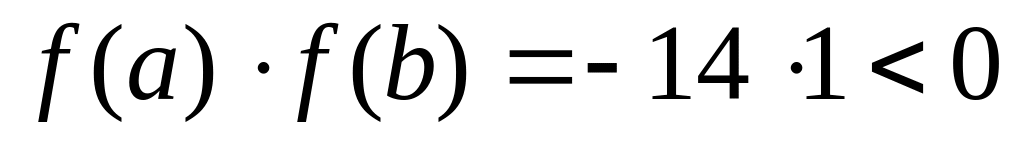 – условие выполняется.
– условие выполняется.Найдём производные:
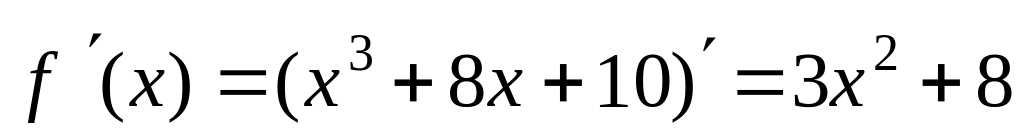 и
и

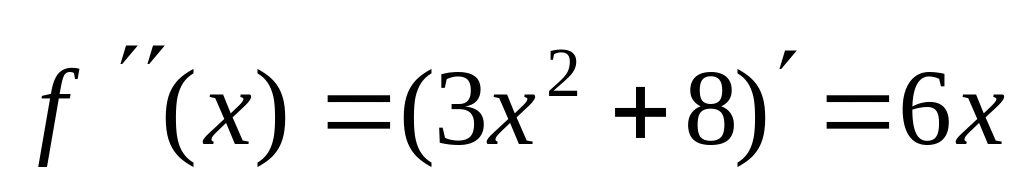 .
.На отрезке производные и , т.е. сохраняют знак, следовательно, условие в) выполняется.
Т.к.
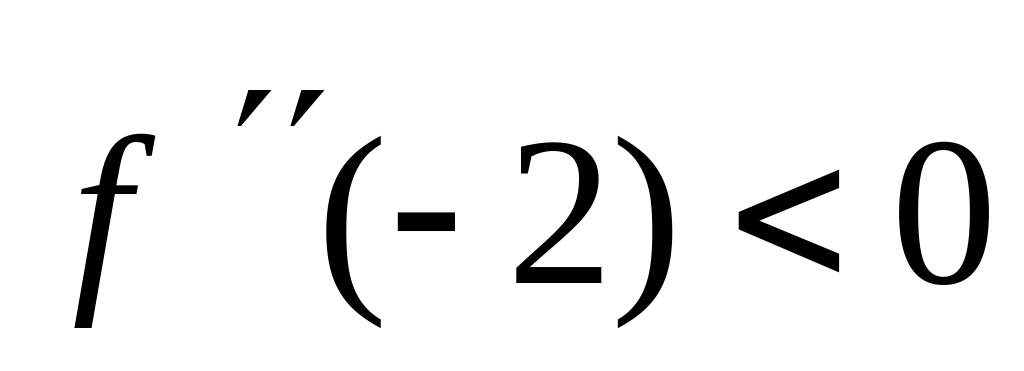 и
и
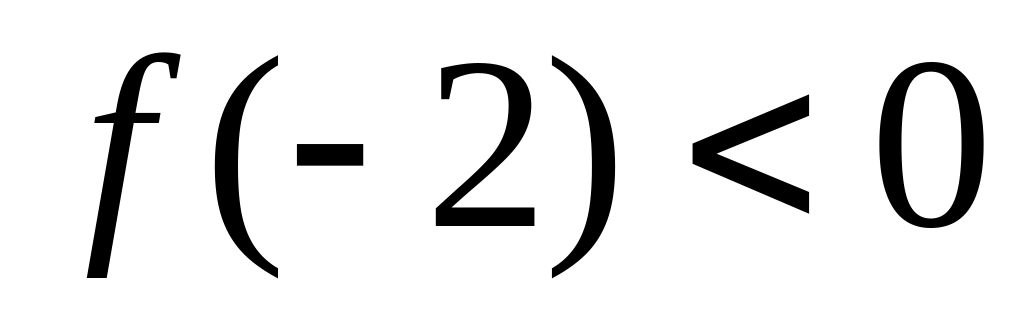 ,
то
,
то
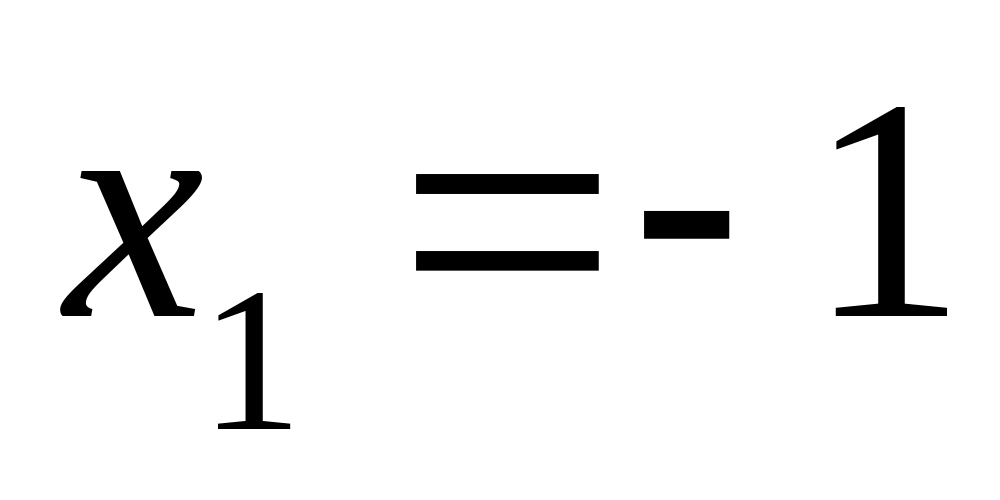 ,
,
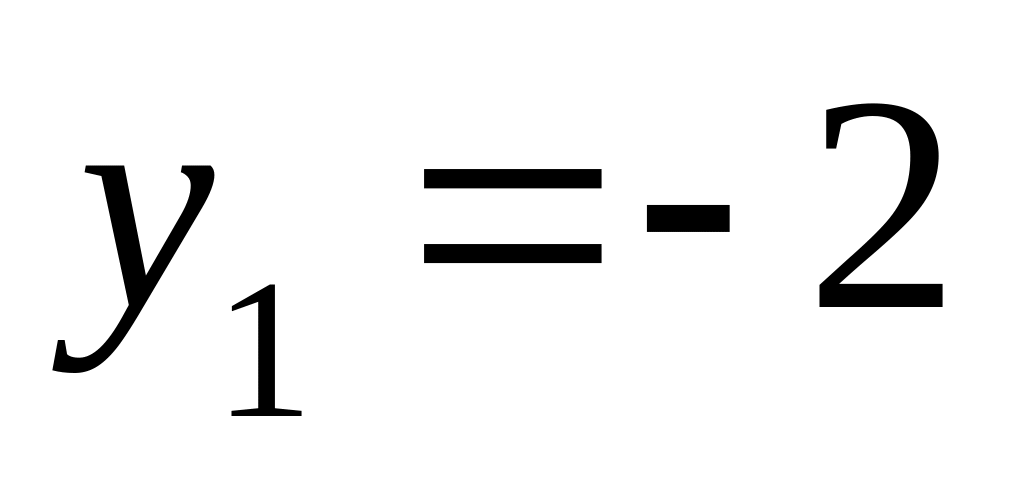 .
.Найдём следующие приближения корня:
а)
по методу касательных:
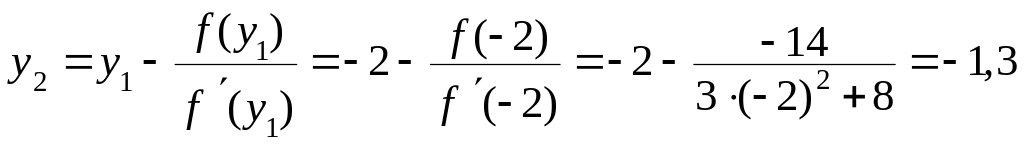
б)
по методу хорд:
![]() .
.
Проверим выполнение условия (1.2):
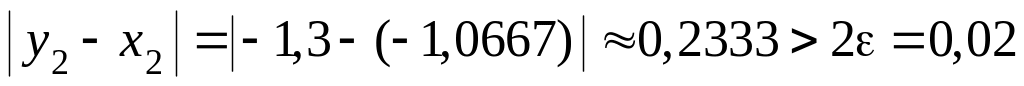 – условие не выполняется, значит нужно
продолжить вычисления.
– условие не выполняется, значит нужно
продолжить вычисления.Новый отрезок изоляции корня имеет вид:
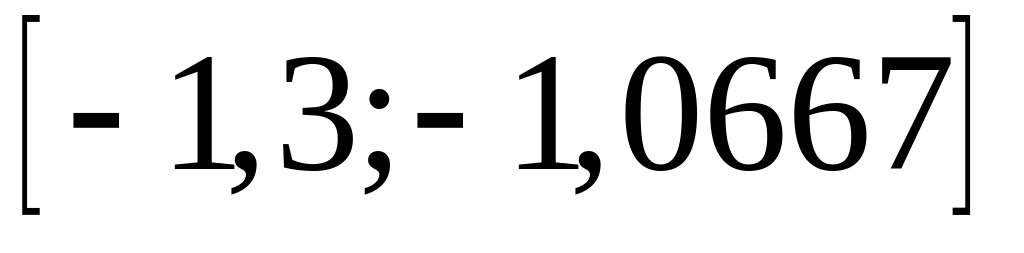 .
.Продолжим сужение отрезка изоляции корня. Для этого найдём значения функции на концах суженного отрезка:
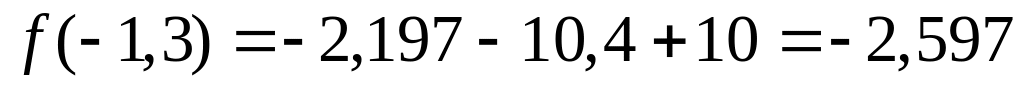 ,
,
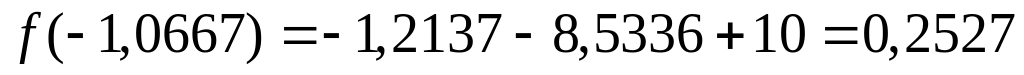 .
.Найдём новые значения концов отрезка изоляции корня:
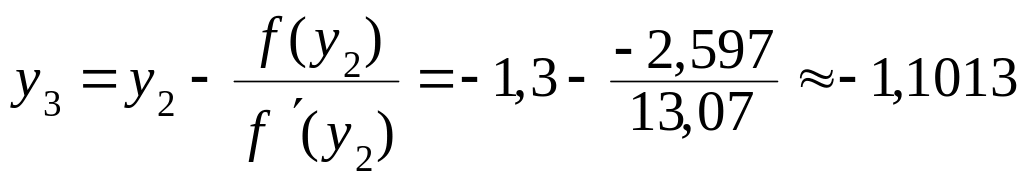 ,
,
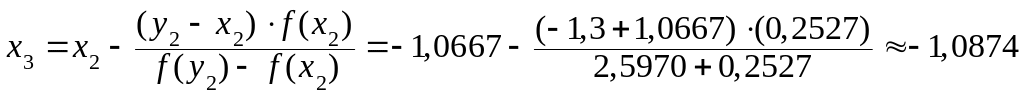 .
.
Проверим выполнение условия:
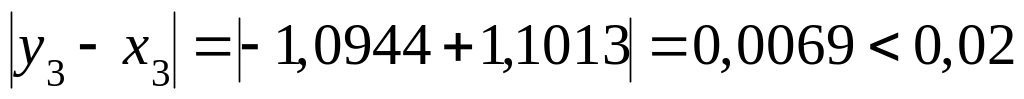 – условие (1.2) выполняется, значит, цель
достигнута.
– условие (1.2) выполняется, значит, цель
достигнута.Найдём приближенное значение корня:
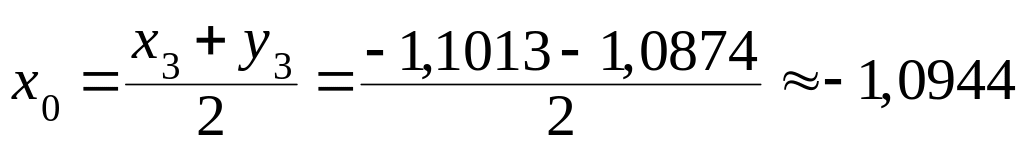 .
.По правилам приближения примем