
- •Молекулярная физика. Термодинамика.
- •Введение
- •1. Статистический и термодинамический методы исследования вещества.
- •Тема 1. Основы молекулярно-кинетической теории газов
- •2. Идеальный газ. Параметры состояния идеального газа.
- •3. Основное уравнение кинетической теории газов.
- •4. Средняя кинетическая энергия поступательного движения молекул. Закон Дальтона.
- •5. Газовые законы. Уравнение Менделеева-Клапейрона.
- •6. Распределение скоростей молекул по Максвеллу. Экспериментальная проверка закона распределения Максвелла.
- •7. Барометрическая формула. Закон распределения Больцмана.
- •8. Определение числа Авогадро из опыта Перрена.
- •10. Распределение энергии по степеням свободы.
- •Тема 2. Явления переноса в газах
- •10. Понятия о явлениях переноса.
- •Средняя длина свободного пробега, эффективный диаметр молекул.
- •11. Диффузия.
- •12. Вязкость (внутреннее трение).
- •13. Теплопроводность.
- •14. Свойства разреженных газов.
- •Тема 3. Первое начало термодинамики
- •15. Основные термодинамические понятия.
- •Внутренняя энергия термодинамической системы.
- •16. Первое начало термодинамики. Работа, совершаемая газом при изменениях объема.
- •17. Теплоемкость газов. Уравнение Майера. Теплоемкость идеального двухатомного газа.
- •18. Применение первого начала термодинамики к изопроцессам.
- •19. Адиабатный процесс. Понятие о политропных процессах.
- •Тема 4. Второе начало термодинамики
- •20. Круговой процесс. Тепловая машина.
- •21. Второе начало термодинамики. Обратимые и необратимые процессы.
- •22. Цикл Карно.
- •23. Термодинамическая шкала температур. Недостижимость абсолютного нуля.
- •24. Энтропия. Приведенная теплота.
- •25. Изменение энтропии при некоторых процессах.
- •26. Энтропия и термодинамическая вероятность. Теорема Нернста.
- •Тема 5. Реальные газы
- •27. Реальные газы. Уравнение Ван-дер-Ваальса.
- •28. Экспериментальные изотермы реального газа. Критическое состояние вещества.
- •29. Внутренняя энергия реального газа. Эффект Джоуля- Томсона.
- •30. Равновесие жидкости и пара. Уравнение Клапейрона-Клаузиуса.
- •Тема 6. Жидкости
- •31. Свойства жидкого состояния вещества.
- •32. Поверхностный слой. Поверхностная энергия. Поверхностное натяжение.
- •33. Явления на границе жидкости и твердого тела.
- •34. Давление под искривленной поверхностью жидкости.
- •35. Капиллярность.
- •36. Жидкие растворы. Осмотическое давление.
- •Тема 7. Твердые тела
- •37. Кристаллические и аморфные тела. Дальний порядок в кристаллах. Физические типы кристаллов.
- •38. Дефекты в кристаллах.
- •39. Силы, действующие между частицами в твердом теле. Тепловое расширение твердых тел.
- •40. Теплоемкость твердых тел.
- •41. Равновесие фаз. Фазовые переходы. Диаграмма состояния.
- •Оглавление.
- •Молекулярная физика. Термодинамика.
10. Распределение энергии по степеням свободы.
Средняя
энергия (из вывода основного уравнения
кинетической теории газов), приходящаяся
на одну молекулу
![]() .
Если считать молекулу шариком (как в
одноатомном газе), то средняя энергия
такой частицы определяется средней
кинетической энергией ее поступательного
движения. Энергию эту можно представить
как сумму трех слагаемых – кинетических
энергий движения молекулы по трем
взаимно перпендикулярным направлениям:
.
Если считать молекулу шариком (как в
одноатомном газе), то средняя энергия
такой частицы определяется средней
кинетической энергией ее поступательного
движения. Энергию эту можно представить
как сумму трех слагаемых – кинетических
энергий движения молекулы по трем
взаимно перпендикулярным направлениям:
![]() ,
,
где x, , z – составляющие скорости молекул по трем осям координат. Из-за хаотичности молекулярного движения можно считать, что средние значения кинетических энергий по трем направлениям равны друг другу:
![]() .
(1)
.
(1)
Так как согласно основному уравнению кинетической теории
![]() ,
,
то каждое из трех слагаемых равенства (1) равно kT/2. Разделение кинетической энергии частицы на три независимые составляющие связано с тем, что частица рассматривается как свободная материальная точка, обладающая тремя степенями свободы.
Число степеней свободы - наименьшее число линейно независимых координат, которые полностью определяют положение тела в пространстве. Значит, на каждую степень свободы одноатомной молекулы приходится энергия, равная kT/2. В классической статистической физике доказывается теорема, названная теоремой Больцмана:
в совокупности большого числа молекул, находящемся в тепловом равновесии при температуре Т средняя кинетическая энергия равномерно распределена между всеми степенями свободы и для каждой степени свободы молекулы она равна kT/2.
Эта теорема называется законом равномерного распределения кинетической энергии по степеням свободы, или, законом равнораспределения.
Двух- и многоатомные газы отличаются от одноатомных числом степеней свободы. Рассмотрим двухатомную молекулу. Ее можно представить себе в виде системы, состоящей из двух атомов, расположенных на некотором расстоянии друг от друга. Будем считать, что это жесткая молекула, то есть расстояние между атомами не меняется.
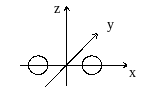
![]() ,
где J
– момент инерции системы, J
mr2.
Величины угловой скорости
вокруг оси 0х, которые могут быть
достигнуты, практически таковы, что
,
где J
– момент инерции системы, J
mr2.
Величины угловой скорости
вокруг оси 0х, которые могут быть
достигнуты, практически таковы, что
![]() значительно меньше кинетической энергии
поступательного движения. Вращение
относительно оси 0х неэффективно. Поэтому
для описания возможных вращений
достаточно двух координат. Следовательно,
число степеней свободы жесткой двухатомной
молекулы равно 5, из них три поступательные
и две вращательные степени свободы. Но
атомы в молекуле не всегда жестко связаны
друг с другом. Об этом мы подробнее
поговорим при изучении теплоемкости
идеального газа. Трехатомный газ имеет
6 степеней свободы. Если молекула состоит
из n атомов, не жестко связанных, то она
имеет 3n степеней свободы (каждый атом
имеет три степени свободы). Из этого
числа три степени свободы поступательные
и три вращательные, за исключением
случая, когда атомы расположены на одной
прямой, – тогда вращательных степени
свободы только две. Остальные 3n-6 степени
свободы являются колебательными.
значительно меньше кинетической энергии
поступательного движения. Вращение
относительно оси 0х неэффективно. Поэтому
для описания возможных вращений
достаточно двух координат. Следовательно,
число степеней свободы жесткой двухатомной
молекулы равно 5, из них три поступательные
и две вращательные степени свободы. Но
атомы в молекуле не всегда жестко связаны
друг с другом. Об этом мы подробнее
поговорим при изучении теплоемкости
идеального газа. Трехатомный газ имеет
6 степеней свободы. Если молекула состоит
из n атомов, не жестко связанных, то она
имеет 3n степеней свободы (каждый атом
имеет три степени свободы). Из этого
числа три степени свободы поступательные
и три вращательные, за исключением
случая, когда атомы расположены на одной
прямой, – тогда вращательных степени
свободы только две. Остальные 3n-6 степени
свободы являются колебательными.
Итак, если
молекула обладает i
степенями свободы, то средняя энергия
молекулы
![]() .
.
