7. Барометрическая формула. Закон распределения Больцмана.

При выводе основного уравнения молекулярно-кинетической теории газов предполагалось, что на молекулы газа внешние силы не действуют, поэтому молекулы равномерно распределены по объему. Если гав находится в силовом поле, то существуют силы, которые сообщают хаотически движущимся молекулам направленное движение.

Молекулы газа, находящиеся в поле тяготения, участвуют в тепловом движении и испытывают действие силы тяжести. Тяготение и тепловое движение приводят к состоянию газа, при котором наблюдается убыль концентрации и давления газа с возрастанием высоты над землей.

Выведем закон изменения давления с высотой, предполагая, что поле тяготения однородно, температура постоянна и масса всех молекул одинакова и равна m₀.

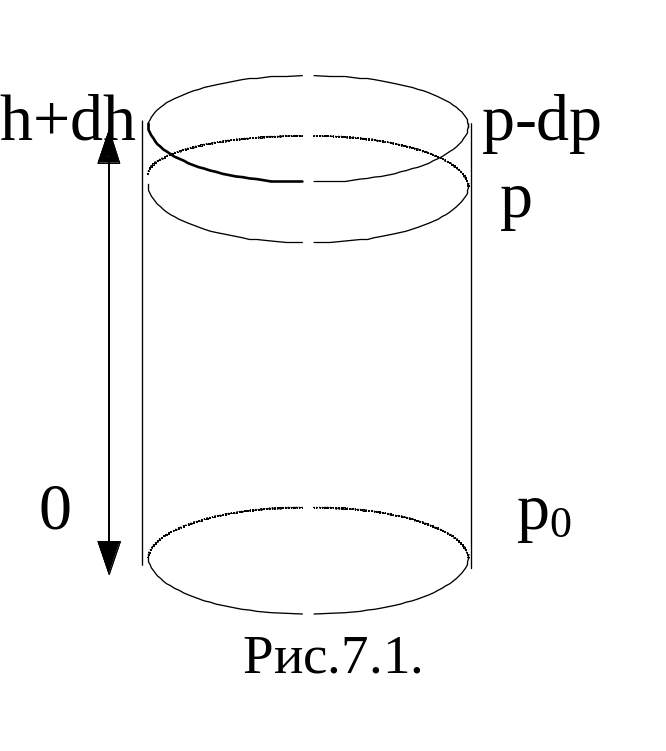
Атмосферное давление на некоторую площадку S обусловлено весом столба воздуха над этой площадкой (т.е. действием силы тяжести). Пусть на высоте h – давление р, а при h=0 – p=p₀. Рассмотрим изменение давления элемента “столба” высотой dh, в пределах которого концентрацию можно считать постоянной. Убыль давления в пределах dh: .

Но , или , поэтому: .

Произведя разделение переменных: , получим

.

Если учесть, что , тогда

.

Зависимость давления атмосферы от высоты над уровнем моря при постоянной температуре называют барометрической формулой.

Пользуясь барометрической формулой , можно получить закон изменения концентрации с высотой. Приняв во внимание и , где n и n₀ – концентрация молекул на высоте h и h₀=0 и подставляя р и р₀ в барометрическую формулу, получим закон распределения концентраций по высоте: ,

Полученное распределение Больцмана справедливо для поля тяготения, для которого – потенциальная энергия на высоте h (на разной высоте молекула обладает различным запасом потенциальной энергии). Однако оно справедливо и для идеального газа, находящегося в любом другом потенциальном поле:

распределение Больцмана в поле с потенциальной энергией U .

При Т , nn₀, то есть происходит выравнивание концентрации газа по всему объему, занимаемому газом. При Т 0, n 0, то есть все молекулы опустятся на поверхность Земли (если речь идет об атмосфере).

8. Определение числа Авогадро из опыта Перрена.

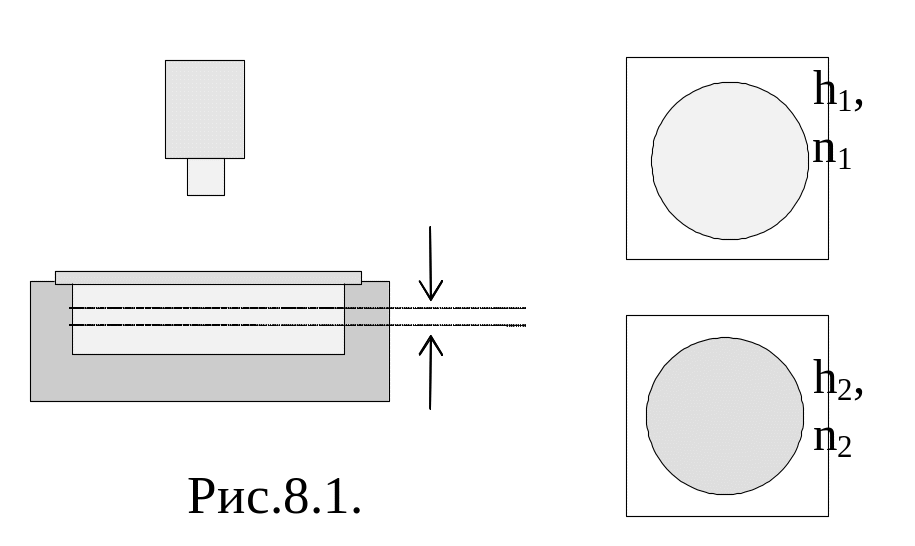Перрен исходил из того, что выводы из молекулярно-кинетической теории справедливы не только для атомов и молекул, но и для броуновских частиц. В подтверждение было показано, что измеренное значение кинетической энергии броуновской частицы действительно оказалось равным .

Перрен предположил, что на “газ” броуновских частиц может быть распространен барометрический закон. Перрен приготовил эмульсию из некоторой смолы (гуммигут - млечный сок деревьев, растущих в Ост.Индии и Цейлоне). Броуновскими частицами были шарики из этой смолы размерами (0,20,5) мкм, причем отделялись (отфильтровывались) частицы с одинаковыми размерами. Эмульсия помещалась в кювету, которая наблюдалась в микроскоп.. Глубина поля зрения порядка одного микрона. Подсчитывалось число частиц на этой высоте. Подсчитывалось число частиц на высотах h₁ и h₂.

, , , .

С учетом Архимедовой силы (на частицу, имеющую плотность порядка =1,2 г/см³ и находящуюся в воде с близкой по величине плотностью ’=1 г/см³, действует выталкивающая сила): .

Таким образом, из эксперимента находится величина k по формуле:

.

Число Авогадро вычисляется из : .

Это был один из первых методов вычисления числа Авогадро. Оно оказалось равным: N_A 6,8.10²³моль^-1. Таким образом, значение, полученное Перреном, находится в согласии с другими полученными значениями, следовательно к броуновским частицам можно применить распределение Больцмана.