25. Изменение энтропии при некоторых процессах.

По первому закону термодинамики: dQ = dU + dА. Известно, что для обратимых процессов: , поэтому dQ=T dS.

Применим эти формулы к идеальному газу: T dS = dU + dА

или .

Используя уравнения Менделеева-Клапейрона: , получим

.

Произведя разделение переменных, получим .

Изменение энтропии при термодинамических процессах в идеальном газе:

.

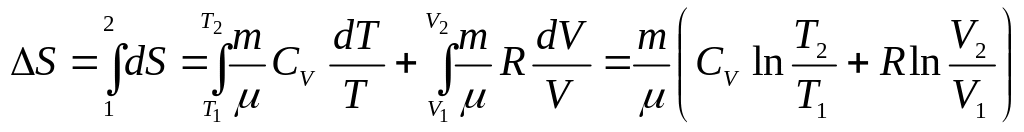Уравнение Менделеева-Клапейрона позволяет выразить изменение энтропии через другие параметры состояния идеального газа:

.

При переходе идеального газа из состояния 1 в состояние 2 изменение энтропии не зависит от типа процесса перехода.

а) Обратимся к изотермическому процессу (Т₁=Т₂) .

Первый закон термодинамики: T dS = dU + dА

dА =T dS - dU=– d(U – T S)= – dF

F= U – T S – третья функция состояния, которая называется свободной энергией.

Свободная энергия – это та часть энергии, которая при обратимом изотермическом процессе может быть полностью обращена в тепло (в работу, так dQ=dA).

б) Для адиабатного процесса: dQ=0, следовательно , то есть при адиабатных процессах энтропия не изменяет своего значения. Поэтому обратимый адиабатный процесс называют также изэнтропическим, а адиабату изэнтропией.

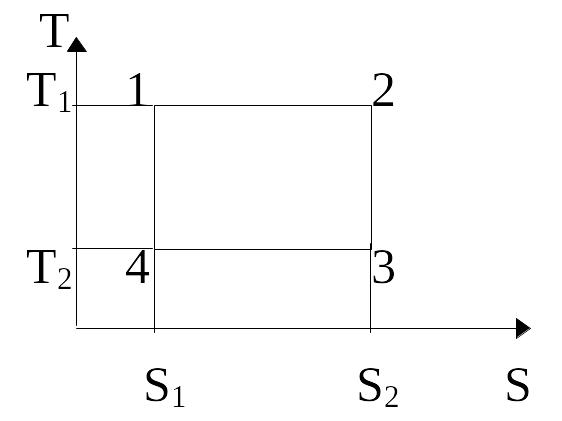
Рассмотрим теперь цикл Карно в переменных не (р, V), а (Т,S).

Q₁₂=T₁(S₂-S₁); Q₃₄=T₂(S₁-S₂)=– T₂(S₂-S₁)

А= Q₁₂ + Q₃₄ =(T₁– T₂)(S₂-S₁)

Мы получили работу идеальной тепловой машины за цикл.

в) При изохорном процессе (V₁=V₂)

г) При изобарном процессе: dQ = dU + pdV

dQ = d(U + pV)=dH, T dS = dH

H= U + pV – четвертая функция состояния – энтальпия.

Изменение энтальпии равно количеству теплоты, которое сообщают системе или отводят от нее при постоянном давлении. DН характеризует тепловые эффекты фазовых переходов, химических реакций и других процессов при постоянном давлении.

26. Энтропия и термодинамическая вероятность. Теорема Нернста.

Понятие энтропии имеет двоякое истолкование: макроскопическое и микроскопическое. Соотношение является макроскопическим определением энтропии. Микроскопический смысл энтропии установил Л.Больцман, который показал, что энтропия является функцией термодинамической вероятности

Термодинамическая система представляет собой ассоциацию громадного числа частиц, микросостояние которых обусловливает состояние макросистемы в целом.

Термодинамическая вероятность системы W- это число всевозможных распределений частиц по координатам и скоростям, соответствующих данному термодинамическому состоянию.

То есть это число микроскопических состояний, которые реализуют данное макросостояние системы. В отличие от математической вероятности, нормированной так, что она не может быть больше единицы, термодинамическая вероятность нормируется так, чтобы все вероятности (если это возможно) выражались целыми числами, то есть W³1.

Для системы, состоящей из  отсеков:

Пусть система мысленно разделена на 2 отсека. Тогда термодинамическая вероятность:

W имеет минимальное значение при n=0 и n=N, то есть когда все частицы в одном отсеке, W максимальна, когда n=N/2, то есть когда частицы распределены по отсекам равномерно.

Таким образом, наиболее вероятное состояние макросистемы соответствует беспорядочному тепловому движению составляющих ее частиц, так как при этом число возможных микросостояний отдельных частиц максимально по сравнению с любыми другими, более упорядоченными формами движения этих частиц. Таким образом, наиболее вероятным является состояние макросистемы, при котором вся энергия переходит в теплоту, равномерно распределенную между телами.

Термодинамическая вероятность и энтропия связаны соотношением (формула Больцмана):

Таким образом, энтропия может рассматриваться как мера вероятности состояния термодинамической системы.

Соответственно второе начало термодинамики может быть сформулировано так: все естественные процессы в изолированной термодинамической системе протекают так, что система переходит от состояний, менее вероятных, к состояниям, более вероятным.

Изменение термодинамической вероятности . Изменение энтропии системы: ,

где W₁ и W₂ - значения термодинамической вероятности в состоянии 1 и 2.

Если процесс обратимый, DW=0 (W=const, )и DS=0, S=const

Если процесс необратимый, DW > 0 ( W – возрастает) и DS > 0 (S – возрастает). Необратимый процесс переводит систему из менее вероятного состояния в более вероятное, в пределе - равновесное состояние, которому соответствует наибольшая термодинамическая вероятность. Энтропия равновесного состояния максимальна. Энтропия является мерой беспорядка системы.

Так как энергия беспорядочного движения частиц газа пропорциональна температуре, то при нуле температуры беспорядочное движение должно прекратиться – частицы будут располагаться наиболее упорядоченным образом. Этой наибольшей упорядоченности расположения частиц должна отвечать наименьшая энтропия. В.Нернст (1864-1941), основываясь на ряде физико-химических наблюдений, высказал положение, часто называемое третьим началом термодинамики: энтропия всех тел в состоянии равновесия стремится к нулю по мере приближения температуры к нулю Кельвина: .

Так как энтропия определяется с точностью до аддитивной постоянной, то эту постоянную удобно взять равной нулю. Отметим, однако, что это произвольное допущение, поскольку энтропия по своей сущности всегда определяется с точностью до аддитивной постоянной. Из теоремы Нернста следует, что теплоемкости С_р и С_V при О К равны нулю.