7.3. Коло з ємністю

Якщо конденсатор ємністю під’єднати до напруги (рис. 7.6), то на пластинах конденсатора зосереджуватиметься заряд, Кл,

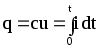. (7.33)

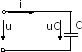
Рис.7.6

Якщо напруга постійна, то при сталому режимі струм у колі не протікатиме, оскільки напруга конденсатора , до якої він зарядився, напрямлена проти прикладеної напруги і врівноважить її. Згідно з другим зако-ном Кірхгофа

. (7.34)

У разі змінної напруги, яка варіює як за величиною, так і за знаком, ємність увесь час перебуватиме в процесі заряджaння або розряджання; при цьому в колі безперервно протікатиме струм, змінюючись як за величиною, так і за напрямком. У провідниках (проводах) протікає струм провідності, у діелектриці конденсатора – струм зміщення, що дорівнює струму провідності.

Диференціюючи математичний вираз (7.33), дістаємо формулу для визначення струму в колі:

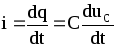(7.35)

Якщо до обкладок конденсатора прикладено синусоїдну напругу

, (7.36)

то струм в даному колі визначиться згідно з (7.35):

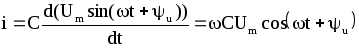(7.37)

або, виразивши через синус, дістанемо

, (7.38)

де

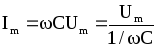; (7.39)

(7.40)

Із (7.40) знаходимо, що кут зсуву фаз між напругою і струмом

. (7.41)

Отже, напруга на ємності відстає від струму, що протікає через цю ємність, на кут, тобто на чверть періоду (рис.7.7). Поділимо обидві частини рівняння (7.39) на :

; (7.42)

де , – діюче значення відповідно струму, що протікає через конденсатор, і напруги на обкладках даного конденсатора. Математичні форму-ли (7.39) і (7.42) – це закон Ома для розглянутого кола.

У розглядуваному випадку величина відіграє роль опору: її називають ємнісним опором, позначають і вимірюють в омах:

; (7.43)

.

Із (7.43) випливає, що ємнісний опір обернено пропорційний до частоти . Зазначимо, що ємнісний опір, як і індуктивний, можна використовувати лише для співвідношень між максимальними та діючими значеннями напруги і струму

Рис.7.7

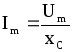(7.44)

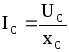(7.45)

і неможливо для миттєвих значень.

Миттєве значення струму та напруги взаємопов’язані диференціальним рівнянням (7.35). Фізично ємнісний опір є протидією сил електричного поля, створеного струмом, що протікає через дану ємність під дією напруги джерела, цьому ж струму.

Енергія, яка нагромаджується в електричному полі ємності дорівнює .

Миттєва потужність

(7.47)

визначає швидкість перетворення енергії джерела на енергію електричного поля конденсатора. Її можна визначити ще й так:

.

Замінимо і діючими значеннями і :

, (7.48)

або

, (7.49)

Із рівняння (7.48) і (7.49) бачимо, що миттєва потужність , так само як і , змінюється за гармонійним законом з подвійною кутовою частотою порівняно з кутовою частотою напруги ( або струму) і коливається в межах від нуля до амплітудного значення

. (7.50)

При цьому, протягом першої і третьої чвертей миттєва потужність додатна (>0). У цьому разі енергія від джерела надходить у коло і нагромаджується у вигляді електричного поля в конденсаторі. Конденсатор при цьому заряджається. У другій і четвертій чвертях періоду миттєва потужність від’ємна (< 0 ). У цьому разі енергія, яку нагромаджено в конденсаторі, повертається знову до джерела. Конденсатор при цьому розряджається. Отже, ємнісний опір, так само як і індуктивний, єнергію, одержану від джерела, не витрачає, а лише нагромаджує в електрично-му полі, а потім повертає назад до джерела. Отже, ємнісний опір нале-жить до реактивних опорів. Середня потужність за період , що одержує коло змінного струму з ємністю ,

=. (7.51)

Отже, в електричному колі змінного струму з ємністю відбувається лише періодичний обмін енергією між джерелом та електричним полем конденсатора без перетворення енергії на теплову або механічну. Струм у такому колі випереджає за фазою напругу на кут і його називають реактивним ємнісним.

Добуток діючих значень напруги та струму називають ємнісною потужністю і позначають :

[вар] (7.52)

Цій потужності приписують знак “ – ”.

Так, якщо поєднати за фазою струм та на рис 7.4 і 7.7, тобто щоб вони збігалися за часом, то неважко переконатися , що чвертям періоду, яким відповідає додатнє значення потужності , відповідатиме від’ємне значення потужності , і навпаки.

Енергія , пов’язана з електричним полем,

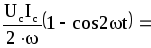
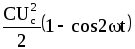==. (7.53)

Тут вважатимемо кут .

Одиниці : 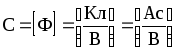, отже,.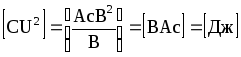

Таким чином, енергія має пульсуючий характер і через кожну половину періоду основної частоти зменьшується до нуля (див. рис. 7.7).