
- •Тема 4. Зображення сигналів змінного струму.
- •Тема 5 Пасивні елементи в найпростіших електричних колах.
- •Лекція 3 Розділ 2 електричні кола змінного струму
- •Тема 6.Основні визначення.
- •6.1. Гармонійні електричні величини
- •Наприклад, для двох синусоїдних функцій часу
- •6.2. Середні та діючі значення періодичних ерс, напруги і струму
- •6.4. Зображення синусоїдних ерс, напруги та струму обертовими векторами. Векторні діаграми
- •Тема 7. Пасивні елементи в найпростіших електричних колах
- •7.1. Коло з активним опором
- •7.2. Коло з індуктивністю
- •Використовуючи для кола (рис. 7.3) другий закон Кірхгофа, дістаємо
- •7.3. Коло з ємністю
Використовуючи для кола (рис. 7.3) другий закон Кірхгофа, дістаємо
![]() .
.
Звідки
![]() .
.
Отже
![]() .
(7.16)
.
(7.16)
Індекс
![]() біля
струму
біля
струму
![]() не пишемо, але пам’ятаємо,
що це струм в індуктивності
не пишемо, але пам’ятаємо,
що це струм в індуктивності
![]() .
.
Припустимо,
що під дією прикладеної до затискачів
(рис. 7.3) напруги через індуктивність
![]() протікає
синусоїдний струм
протікає
синусоїдний струм
![]() .
Знайдемо
напругу
.
Знайдемо
напругу
![]() ,
що спричиняє даний струм. Для цього в
(7.16) підставимо значення струму
,
що спричиняє даний струм. Для цього в
(7.16) підставимо значення струму
![]() і в результаті дістанемо
і в результаті дістанемо
![]()
![]()
![]() .
(7.17)
.
(7.17)
Або
виразимо
![]() через
синус
через
синус
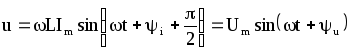 ,
(7.18)
,
(7.18)
де
![]() ;
(7.19)
;
(7.19)
![]() .
(7.20)
.
(7.20)
Із
формули ( 7.20) знаходимо
![]() .
.
Тоді
кут зсуву фаз
![]() .
(7.21)
.
(7.21)
Отже,
напруга на індуктивності випереджає
за фазою струм у ній на кут
![]() ,
тобто на чверть періоду (рис. 7.4,а). Із
формули (7.19) маємо
,
тобто на чверть періоду (рис. 7.4,а). Із
формули (7.19) маємо
![]() .
(7.22)
.
(7.22)
або,
поділивши обидві частини рівняння на
![]() ,
дістанемо
,
дістанемо
![]() .
(7.23)
.
(7.23)
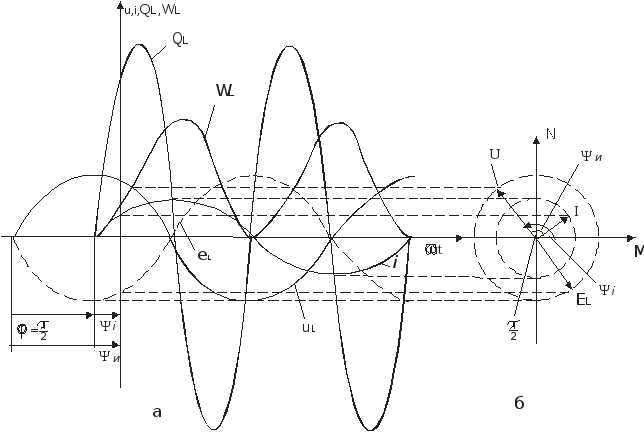
Рис.7.4
Індекси
![]() біля
діючих значень струму і напруги поставлені
для того, щоб
біля
діючих значень струму і напруги поставлені
для того, щоб
підкреслити,що напругу прикладено до котушки індуктивності і струм протікає саме в ній. Формули (7.22) і (7.23) – це закон Ома для досліджу-ваного кола.
Часові та векторні діаграми цього кола показано на рис. 7.4.
Величина
![]() відіграє
роль опору. Її називають індуктивним
опором, позначають
відіграє
роль опору. Її називають індуктивним
опором, позначають
![]() і
вимірюють в омах:
і
вимірюють в омах:
![]() ;
(7.24)
;
(7.24)
[ω] =[1/c]; [L]=[Гн]=[Ом∙с], отже, [1/c∙Ом∙с]=[Ом].
Величина
![]() зростає
зі збільшенням
зростає
зі збільшенням
![]() у прямій
пропорції (рис.7.5).
у прямій
пропорції (рис.7.5).
Фізично індуктивний опір виражає протидію ЕРС самоіндукції змінному струму, яка виникає при протіканні останнього через індуктивність.
Енергія,
що нагромаджується
в магнітному колі індуктивності,
дорівнює
![]() .
.
Миттєва потужність
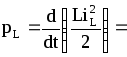
![]() .
(7.26)
.
(7.26)
визначає швидкість перетворення енергії джерела (генератора) на енергію магнітного поля індуктивності. Визначимо її:
![]()
![]() .
.
Замінивши
![]() і
і
![]() діючими значеннями
діючими значеннями
![]() і
і
![]() ,
дістаємо
,
дістаємо
![]() (7.27)
(7.27)
або
![]() .
(7.28)
.
(7.28)
Із
рівняння (7.27) і (7.28) бачимо, що миттєва
потужність
![]() змінюється
згідно з гармонійним законом з подвійною
кутовою частотою струму
змінюється
згідно з гармонійним законом з подвійною
кутовою частотою струму
![]() порівняно
з кутовою частотою струму (або напруги)
і коливається в межах від нуля до
амплітудного значення
порівняно
з кутовою частотою струму (або напруги)
і коливається в межах від нуля до
амплітудного значення
![]() .
(7.29)
.
(7.29)
Зазначимо,
що протягом першої і третьої чвертей
періоду миттєва потужність додатня
![]() >0.
При цьому енергія від джерела надходить
у коло і нагромаджується у вигляді
енергії магнітного поля в котушці
індуктивності. У другій і четвертій
чвертях періоду миттєва потужність
від’ємна (
>0.
При цьому енергія від джерела надходить
у коло і нагромаджується у вигляді
енергії магнітного поля в котушці
індуктивності. У другій і четвертій
чвертях періоду миттєва потужність
від’ємна (![]() <
0). При цьому вся нагромаджена в
індуктивності енергія повертається
назад до джерела (див. рис. 7.4).
<
0). При цьому вся нагромаджена в
індуктивності енергія повертається
назад до джерела (див. рис. 7.4).
Опори,
в яких не витрачається одержана від
джерела енергія, а лише нагромаджується,
а потім повертається назад до джерела,
називають реактивними. Отже, індуктивний
опір
![]() належить
до реактивних опорів.
належить
до реактивних опорів.
Середня,
тобто активна, потужність
![]() за
період
за
період
![]() ,
яку одержує коло змінного струму з
індуктивністю
,
яку одержує коло змінного струму з
індуктивністю
![]() ,
,
![]() .
(7.30)
.
(7.30)
Отже,
в електричному колі змінного струму з
індуктивністю
![]() відбувається лише періодичний обмін
енергією між джерелом і магнітним полем
котушки без перетворення електромагнітної
енергії на теплову або механічну.
відбувається лише періодичний обмін
енергією між джерелом і магнітним полем
котушки без перетворення електромагнітної
енергії на теплову або механічну.
Струм,
який протікає в такому колі, відстає
від напруги за фазою на кут
![]() і його
називають реактивним.
і його
називають реактивним.
Добуток
діючих значень напруги
![]() і
струму
і
струму
![]() називають
реактивною потужністю і позначають
називають
реактивною потужністю і позначають
![]() :
:
![]() .
(7.31)
.
(7.31)
Реактивну потужність вимірюють у вольт-амперах реактивних (вар).
Енергія, пов’язана з магнітним полем котушки індуктивності,
![]() =
=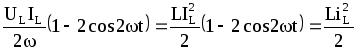 =
=![]() (7.32)
(7.32)
Тут
вважатимемо кут
![]() .
.
Одиниці
![]()
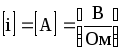 ,
,
Таким
чином, енергія
![]() має
пульсуючий характер і через кожну
половину періоду основної частоти
має
пульсуючий характер і через кожну
половину періоду основної частоти
![]() зменшується
до нуля (див. рис. 7.4).
зменшується
до нуля (див. рис. 7.4).
