
- •Содержание
- •Введение в анализ
- •§ 1. Функции и последовательности
- •§ 2. Предел функции
- •Окрестности точек числовой прямой
- •Определение предела функции
- •Основные свойства пределов
- •§ 3. Бесконечно малые функции
- •1. Бесконечно малые и их свойства
- •2. Бесконечно большие функции
- •3. Виды неопределенностей и замечательные пределы
- •4. Вычисление пределов с помощью эквивалентных бесконечно малых
- •§ 4. Непрерывность функций
- •1. Понятие непрерывной функции
- •2. Свойства функций, непрерывных в точке
- •3. Точки разрыва и их классификация
- •4. Односторонняя непрерывность
- •5. Свойства функций, непрерывных на отрезке
3. Точки разрыва и их классификация
Если функция f(x) не является непрерывной в точке x0, то точка x0 называется точкой разрыва функции f(x).
Согласно определению функции, непрерывной в точке x0, в точке разрыва функция либо не определена, либо не имеет в этой точке конечного предела, либо конечный предел функции в точке x0 существует, но не совпадает со значением f(x0) функции f(x) в этой точке.
Точка разрыва x0 функции f(x) называется точкой разрыва первого рода, если f(x) имеет в этой точке конечные односторонние пределы и . При этом если в точке разрыва x0 = , то разрыв называется устранимым, если же , то разрыв называется неустранимым. Разность – называется скачком функции f(x) в точке x0.
Все точки разрыва, не являющиеся точками разрыва первого рода называются точками разрыва второго рода. В точке разрыва второго рода хотя бы один из односторонних пределов не существует или является бесконечным.
20
Разрывы I рода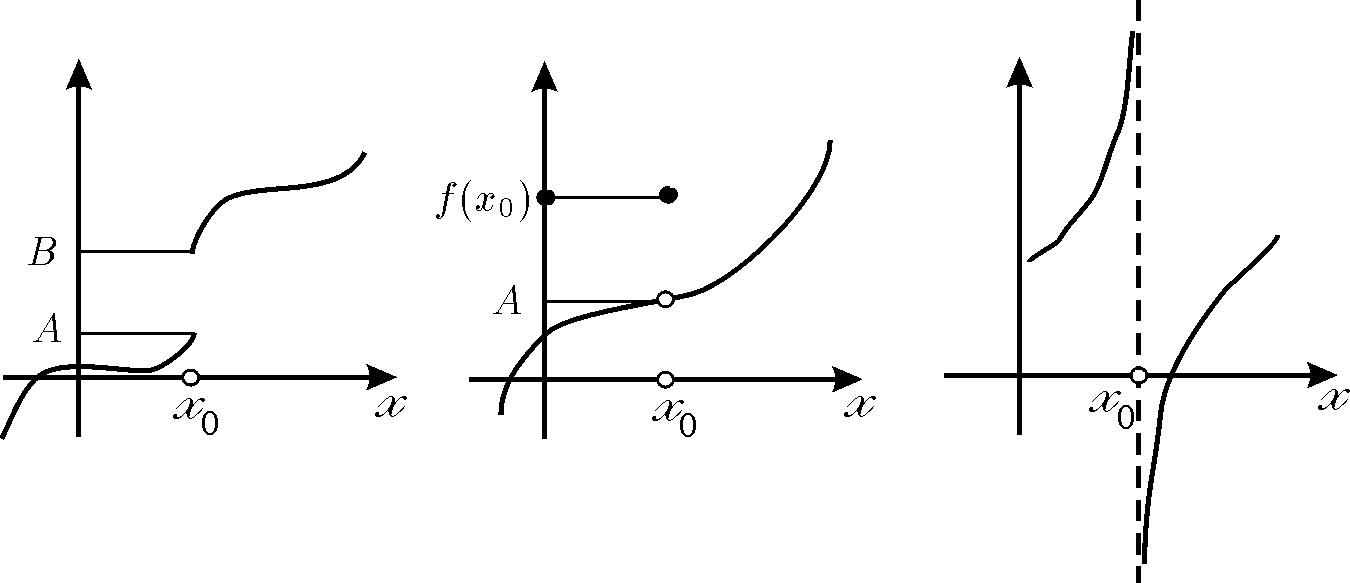
Разрыв неустранимый Разрыв устранимый Разрыв II рода
Если функция f(x)
имеет в некоторой точке x0
устранимый разрыв, то его можно устранить,
переопределив или доопределив функцию
в точке x0.
Например, функция
![]() не определена в точке x
= 0, но имеет в этой точке конечные
односторонние пределы
не определена в точке x
= 0, но имеет в этой точке конечные
односторонние пределы
![]() =
=![]() =
1, так как
.
Значит эта функция имеет в точке x
= 0 устранимый разрыв. Доопределив эту
функцию в точке x = 0
значением 1, то есть, задав значение f(0)
= 1, получим непрерывную в точке x
= 0 функцию.
=
1, так как
.
Значит эта функция имеет в точке x
= 0 устранимый разрыв. Доопределив эту
функцию в точке x = 0
значением 1, то есть, задав значение f(0)
= 1, получим непрерывную в точке x
= 0 функцию.
4. Односторонняя непрерывность
Введем понятие односторонней непрерывности.
Функция f(x) называется непрерывной в точке x0 справа (слева), если выполнены условия:
1. f(x) определена в точке x0,
2. существует конечный предел
![]()
![]() ,
,
3.
=
f(x0)
![]() .
.
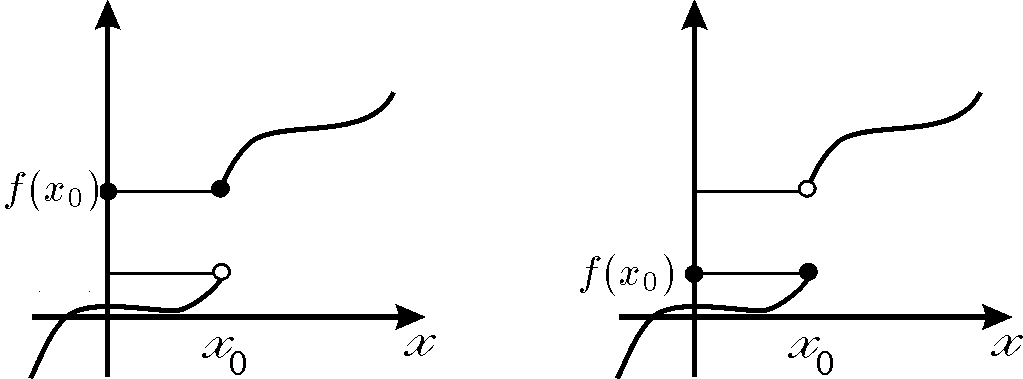
Непрерывность справа Непрерывность слева
21
ТЕОРЕМА. Для того чтобы функция f(x) была непрерывной в точке x0 необходимо и достаточно, чтобы она была в этой точке непрерывной справа и слева.
Доказательство проведите самостоятельно.
5. Свойства функций, непрерывных на отрезке
Если функция f(x) непрерывна в каждой точке некоторого множества D, то она называется непрерывной на этом множестве. Особенно важными являются свойства функций, непрерывных на отрезке. Функция является непрерывной на отрезке [a, b], если она непрерывна в каждой точке интервала (a, b), непрерывна справа в точке a и непрерывна слева в точке b.
ТЕОРЕМА Вейерштрасса.
Всякая непрерывная на отрезке [a, b] функция ограничена на нем и достигает в некоторых точках этого отрезка своего наибольшего и своего наименьшего значений.
Вместо доказательства дадим геометрическую интерпретацию теоремы.

Рис. 1 Рис. 2.
На рис. 1. функция непрерывна на [a, b], ограничена на этом отрезке числами m и M, достигает наибольшего значения M в точке x0, наименьшего значения m в точке a.
На рис. 2. изображена функция, непрерывная
на промежутке [a, b).
В точке b непрерывности
нет, поскольку
![]() .
Функция не ограничена сверху, не имеет
наибольшего значения. Как видим, условие
непрерывности функции на всем отрезке,
включая концы, является существенным.
.
Функция не ограничена сверху, не имеет
наибольшего значения. Как видим, условие
непрерывности функции на всем отрезке,
включая концы, является существенным.
ТЕОРЕМА Больцано-Коши.
Если функция f(x) определена и непрерывна на отрезке [a, b] и принимает на концах отрезка значения A и B (A B), тогда для любого числа C, находящегося между A и B, найдется такое число c, принадлежащее интервалу (a, b), что f (c) = C.
Вместо доказательства дадим геометрическую интерпретацию теоремы.
22

Рис. 3 Рис. 4.
На рис. 3. функция непрерывна на [a, b] и принимает значение C в точке c.
На рис. 4. функция определена на отрезке [a, b] и непрерывна во всех точках этого промежутка, кроме точки x0. Поэтому число C, находящееся между A и B, не является значением данной функции ни в одной точке интервала (a, b).
23
