Глава 1. Задача контактного кручения для стержня

1.1 Постановка задачи

В настоящей работе нас будут интересовать максимальные локальные нормальные и касательные напряжения, возникающие в зоне контакта приложенных напряжений с цилиндром. Величина этих напряжений будет зависеть от степени деформации и от упругих свойств материала стержня. Поэтому изначально решение будем строить в перемещениях, а затем, используя реологическую модель линейного упругого тела, найдем компоненты тензора искомых напряжений внутри тела.

Уравнения равновесия в перемещениях, записанные в цилиндрических координатах, имеют вид [1]:

. (1)

, (2)

. (3)

u,v, w– окружное, радиальное и осевое смещения точки; r, φ, z – цилиндрические координаты; ρ – плотность среды; f_r, f_φ, f_z – проекции массовой силы на оси выбранной системы координат; – объемная деформация; ; – модуль упругости при сдвиге; ν – коэффициент Пуассона; E – модуль Юнга; – оператор Лапласа.

В дальнейшем будем полагать, что нагрузки, прилагаемые к контактирующим элементам системы, настолько значительны, что их собственным весом по сравнению с нагрузками можно пренебречь, а силы электромагнитной природы вообще отсутствуют, так что

.

Следует сказать, что при формулировке задач теории упругости в компонентах перемещений как основных функций уравнения совместности деформаций удовлетворяются автоматически [2, с. 50].

1.2 Разностная схема

Аппроксимируя уравнения (1)– (3)симметричными разностями на неравномерной сетке, получим

. (4)

, (5)

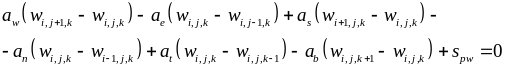. (6)

где , ,

, ,

, ;

Рис 1. Шаблон разностной сетки. Стрелками показаны направления возрастания индексов

Из разностных уравнений (4), (5) получаем следующие рекуррентные формулы для определения значений перемещений во внутренних точках:

, (7)

, (8)

, (9)

которая может быть использована при проведении расчетов по методу простой итерации. Здесь .

1.3 Построение разностной сетки

Строим экспоненциально сгущающуюся на пятне контакта сетку, следуя преобразованиям

(10)

Пусть N – число точек разбиения по радиусу, M₁ – 1 – число секторов впервой четверти, K – число точек разбиения по осевой координате. Тогда

(11)

(12)

(13)

Здесь h, R – высота и радиус цилиндра; δ, ε, γ – параметры преобразования (малые величины).

Рис. 2. Сгущение плоской сетки в окрестности зон контакта

Глава 2. Плоская задача «чистого» контактного кручения

2.1 Постановка плоской задачи.

Рассмотрим деформацию стержня в случае, когда контактные напряжения направлены по касательной к боковой поверхности стержня и перпендикулярно его оси, тогда v = w = 0 и возможен режим «чистого» кручения, то есть когда для решения задачи достаточно проинтегрировать лишь уравнение (1). Если при этом ещё граничные условия не зависят от z-координаты, то задача становится плоской, то есть . В этом случае тензоры деформаций и напряжений будут иметь в качестве ненулевых лишь компоненты:

, (14)

а также σ_φφ и σ_rφ.

Запишем обобщенный закон Гука [2]:

(15)

Здесь предполагается, что по индексу k выполнено суммирование. При этом , – коэффициенты Ляме. Из последнего соотношения находим, что

. (16)

В рассматриваемом нами случае «чистого» кручения уравнение (1) принимает вид

. (17)

Причем . Учитывая последнее обстоятельство, вместо (17) окончательно получим:

. (18)

Здесь введено обозначение .

Уравнение (18) будем интегрировать при следующих граничных условиях:

; (19)

, (20)

. (21)

Причем параметр φ₀ определяет размер пятна контакта.

Заметим, что при интегрировании уравнения (18) на круге или кольце необходимо использовать условие периодичности:

. (22)

Таким образом, речь идет о решении первой граничной задачи, состоящей в определении перемещений и напряжений внутри тела, если известны напряжения на его границе.