Лабораторная работа № 2 исследование приемников однофазного синусоидального тока

Цель работы: экспериментальное определение параметров пассивных элементов электрической цепи; исследование цепи при смешанном соединении приемников.

Теоретические сведения

Пассивными элементами являются: резисторы, катушки индуктивности, конденсатора.

Индуктивная катушка обладает активным сопротивлением R _к и индуктивностью L (рис.1, а), поэтому катушку на схеме замещения представляют последовательной R, L -цепью рис. 1, б).

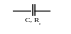
а) б) в)

Рис.1

Параметры R_к, L вычисляются по измеренным значениям напряжения, тока и сдвигу фаз между ними по формулам: полное сопротивление катушки

активное сопротивление катушки

реактивное сопротивление катушки

индуктивность катушки .

Параметрами конденсатора являются активное сопротивление R и емкость С (рис.1,в), которые можно определить, измерив напряжение на конденсаторе ток и сдвиг фаз между ними:

Разветвленная цепь однофазного синусоидального

тока

Расчет цепи переменного тока существенно облегчается, если синусоидально изменяющиеся токи, напряжения, ЭДС и т.д. изображать векторами и комплексными числами. Тогда все методы расчета цепей постоянного тока применимы к расчету цепей синусоидального тока.

Н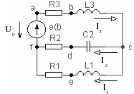 а примере смешанного соединения элементов цепи покажем определение всех токов и напряжений в ней. Токи в такой цепи проще всего рассчитать путем преобразования схемы. Пусть заданы сопротивления всех ее элементов и напряжение U на ее входе (рис. 2); требуется определить токи во всех ветвях цепи.

Рис.2

Преобразуем схему электрической цепи в эквивалентную (рис.3), для этого определим комплексные сопротивления ветвей в алгебраическом и показательном виде:

первой ветви Z₁= R₁ +jX_L1= = z₁e^jφ1,

второй ветви Z₂ = R₂ - jX_C2 = = z₂e^jφ2,

третей ветви Z₃= R₃ + jX_L3 = = z₃e^jφ3 .

Заменим параллельно соединенные первую и вторую ветви одной эквивалентной ветвью с комплексным сопротивлением:

После этого преобразования схема состоит из двух последовательно соединенных сопротивлений Z₃ и Z`(рис. 4).

Общее эквивалентное сопротивление цепи найдем по формуле: Z = Z₃ + Z₁₂` = (R<sub>3</sub> + j X<sub>L3</sub> ) + Z<sub>12</sub>`.

Ток в неразветвленной части цепи определяем по закону Ома

İ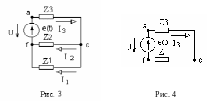 ₃ = Ù / Z.

Напряжение на параллельном соединении ветвей

Ù_{c f} = Z₁₂` İ ₃.

Токи в параллельно соединенных приемниках

İ₁ = Ù_сf / Z ₁, İ₂ = Ù_cf / Z ₂.

Построение векторной диаграммы

Векторной диаграммой называется совокупность векторов на комплексной плоскости, изображающих синусоидально изменяющиеся функции времен одной и той же частоты и построенные с соблюдением правильной ориентации их относительно друг друга по фазе. Вектора на комплексной плоскости откладывают из начала координат. Длина вектора соответствует в масштабе значению функции, угол – начальной фазе. Например, рассчитанный ток равен İ = I e^jφ_i = 2 е^j30°А, построение векторной диаграммы на комплексной плоскости приведен на рис.5 а. Векторные диаграммы тока и напряжения удобнее строить в одних осях координат. Напряжение на резисторе совпадает по направлению с током, протекающим через него, поэтому вектор напряжения изображается одинаково направленным с вектором тока (рис. 5, б).

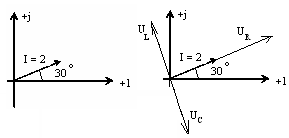
а) б)

в)

Рис.5

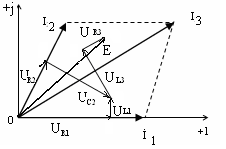
Напряжение на конденсаторе отстает тока на 90°, поэтому U_с сдвигается относительно тока на 90°(по направлению часовой стрелки, рис.5, б) Напряжение на индуктивности опережает ток на 90°, поэтому U_L сдвигается относительно тока на 90°(против направления движения часовой стрелки, рис.5,б). По векторной диаграмме можно проверить выполнение первого и второго законов Кирхгофа. Для проверки второго закона строится цепочка из векторов, следующих один за другим по обходу контура. Вектора переносятся параллельно себе так, чтобы конец одного совпадал с началом другого. Для электрической цепи (рис.2) векторная диаграмма приведена на рис.5, в.