
- •Матрицы. Системы линейных уравнений
- •1. Матрицы
- •1.1. Основные понятия
- •1.2. Действия с матрицами
- •1.3. Задачи
- •2. Определители
- •2.1. Основные понятия
- •2.2. Свойства определителя
- •2.3. Алгебраические дополнения. Миноры. Формулы разложения определителя по столбцу или строке
- •2.4. Вычисление определителей
- •2.5. Задачи
- •3. Обратная матрица
- •3.1. Задачи
- •4. Ранг матрицы
- •4.1. Основные понятия
- •4.2. Вычисление ранга матрицы
- •4.3. Задачи
- •5. Системы линейных уравнений
- •5.1. Основные определения
- •5.2. Квадратные системы. Формулы Крамера
- •5.3. Метод Гаусса
- •5.4. Задачи
- •6. Однородные линейные системы
- •6.1. Общее решение однородной системы
- •6.2. Задачи
- •7. Неоднородные системы
- •7.1. Общее решение неоднородной системы
- •7.2. Задачи
- •Литература
![]() Федеральное
агентство по образованию РФ
Федеральное
агентство по образованию РФ
ТОМСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ
УТВЕРЖДАЮ
Декан ФПМК
________ А. М. Горцев
26 февраля 2007 г.
Матрицы. Системы линейных уравнений
Учебно-методическое пособие
Томск
2007
РАССМОТРЕНО и УТВЕРЖДЕНО методической комиссией факультета прикладной математики и кибернетики.
ПРОТОКОЛ № 26 от 26 января 2007 г.
Председатель комиссии
профессор С.Э.Воробейчиков
В учебно-методическом пособии приведены краткие теоретические сведения и даны практические рекомендации к решению задач по курсу «Линейная алгебра и аналитическая геометрия».
Пособие разработано для студентов факультета прикладной математики и кибернетики дневной формы обучения.
Составители: К.И.Лившиц
Л.Ю.Сухотина

1. Матрицы
1.1. Основные понятия
Определение.
Пусть
![]() — множество чисел и
— множество чисел и
![]() — набор из
— набор из
![]() элементов множества
.
Прямоугольная таблица
элементов множества
.
Прямоугольная таблица
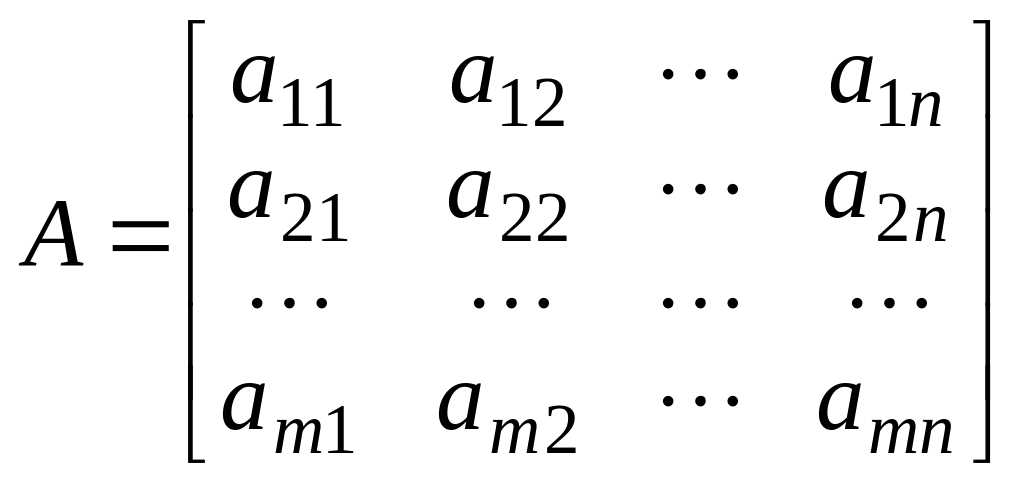 ,
,
состоящая из
![]() строк и
строк и
![]() столбцов, называется матрицей.
столбцов, называется матрицей.
Числа
,
входящие в состав данной матрицы,
называются ее элементами.
Совокупность элементов
![]() образуют
образуют
![]() ю
строку
матрицы, а совокупность элементов
ю
строку
матрицы, а совокупность элементов
![]() образует
образует
![]() й
столбец
матрицы. Величины
и
называются порядками
матрицы.
й
столбец
матрицы. Величины
и
называются порядками
матрицы.
Две матрицы, имеющие
одинаковое число
строк и одинаковое число
столбцов называются матрицами одинакового
типа. Две матрицы
![]() и
и
![]() называются равными,
если они имеют одинаковые порядки и
называются равными,
если они имеют одинаковые порядки и
![]() .
.
Если
![]() ,
матрица называется квадратной.
Совокупность элементов
,
матрица называется квадратной.
Совокупность элементов
![]() называется главной
диагональю матрицы.
Квадратная матрица, у которой отличны
от нуля лишь элементы главной диагонали,
называется диагональной.
Если все диагональные элементы
диагональной матрицы
называется главной
диагональю матрицы.
Квадратная матрица, у которой отличны
от нуля лишь элементы главной диагонали,
называется диагональной.
Если все диагональные элементы
диагональной матрицы
![]() ,
то диагональная матрица называется
единичной
и обозначается символом
,
то диагональная матрица называется
единичной
и обозначается символом
![]() .
.
Матрица, у которой
все элементы равны нулю, называется
нулевой
матрицей и обозначается
![]() .
Нулевые матрицы различных порядков
считаются различными, так как состоят
из разного числа элементов.
.
Нулевые матрицы различных порядков
считаются различными, так как состоят
из разного числа элементов.
Квадратная матрица
называется верхней
треугольной,
если из
![]() следует, что
следует, что
![]() и нижней
треугольной,
если из
и нижней
треугольной,
если из
![]() следует, что
.
следует, что
.
Матрицу, состоящую
из одной строки, называют вектор
— строкой,
а матрицу, состоящую из одного столбца,
называют вектор
— столбцом.
Например, матрица
![]() вектор — строка размера
вектор — строка размера![]() .
.
1.2. Действия с матрицами
1. Транспонирование
матриц.
Операция транспонирования матриц
состоит в перемене местами строк и
столбцов с сохранением их номеров. Пусть
дана матрица
порядка
![]() .
Тогда транспонированной
по отношению матрице
.
Тогда транспонированной
по отношению матрице
![]() называется матрица
порядка
называется матрица
порядка
![]() ,
элементы которой
,
элементы которой
![]() .
Транспонирование матрицы обозначается
как
.
Транспонирование матрицы обозначается
как
![]() .
.
Пример.
Пусть
![]() Тогда
Тогда

2. Сложение матриц.
Операция
сложения вводится только для матриц
одинакового типа. Суммой
двух матриц
и
одинакового типа называется матрица
![]() того же типа, элементы которой
того же типа, элементы которой
![]() Используется обозначение
Используется обозначение
![]() .
.
3. Умножение
матрицы на число. Произведением
матрицы
порядка
и числа
![]() называется матрица
называется матрица
![]() того же типа, элементы которой
того же типа, элементы которой
![]() .
Используется обозначение
.
Используется обозначение
![]() .
.
Пример. Пусть
![]()
Тогда матрица
![]()
4. Умножение
матрицы на матрицу.
Операция умножения матрицы
![]() на матрицу
вводится для прямоугольных матриц при
условии, что число столбцов матрицы
равно числу строк матрицы
на матрицу
вводится для прямоугольных матриц при
условии, что число столбцов матрицы
равно числу строк матрицы
![]() .
Произведением
матрицы
порядка
.
Произведением
матрицы
порядка
![]() и матрицы
порядка
и матрицы
порядка
![]() ,
заданных в определенном порядке (
— первая,
— вторая), называется матрица
,
заданных в определенном порядке (
— первая,
— вторая), называется матрица
![]() порядка
,
элементы которой
порядка
,
элементы которой
![]()
Таким образом,
элемент
![]() матрицы
матрицы
![]() есть сумма произведений элементов
есть сумма произведений элементов
![]() - й строки матрицы
на соответствующие элементы
- й строки матрицы
на соответствующие элементы
![]() - го столбца матрицы
.
- го столбца матрицы
.
Пример 1.
Пусть
![]() .
Тогда
.
Тогда
![]() ,
,
![]() .
.
Пример 2. Пусть
![]() .
Тогда
.
Тогда
![]() .
.
