ФСС 3, 4

(Конспект)

©В.Е.Рок 2011

Деформации сплошной среды

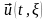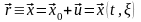При деформации сплошной среды в окрестностях некоторой точки P₀ (при t=0) эта точка в эйлеровой СК переместится к моменту t>0 в положение P, а соседняя с P₀ точка P’₀ - в P’. Зная векторное поле смещений в лагранжевой СК для эйлеровых координат точки P справедливо: а смещение из т. P в т. P’, учитывая их исходную близость в лагранжевой СК :

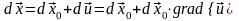
(градиент вектора смещения вычисляется в лагранжевых координатах, сопутствующих частицам сплошной среды).

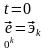
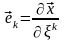
С помощью оператора Гамильтона «набла» можно записать

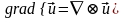
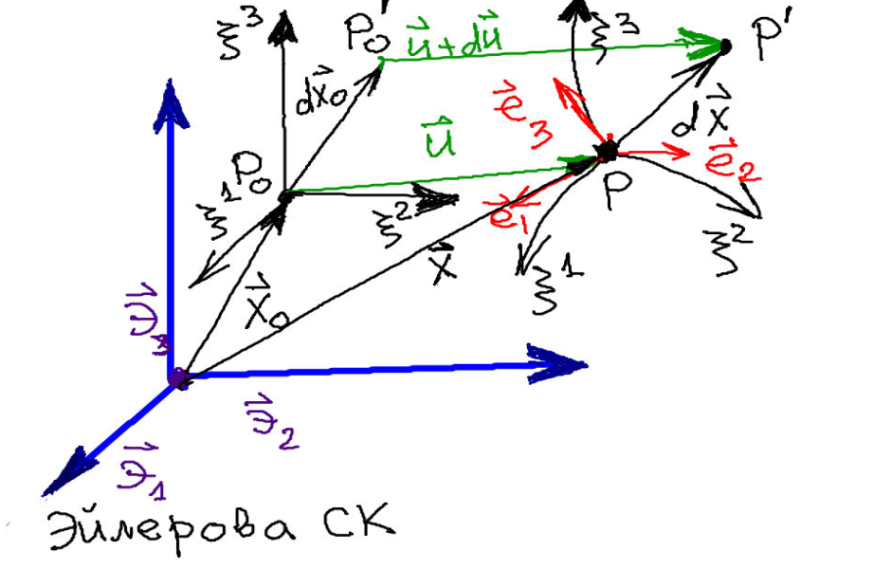
с другой стороны в начальном положении

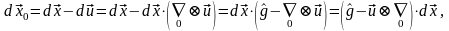
где градиент 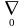вычисляется по координатам в момент t=0, совпадающим с эйлеровыми!

Квадрат расстояния между точками P’ и P в момент t:

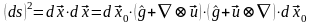
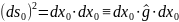
Его изменение к моменту t от момента t=0:

Где

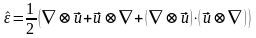
- тензор деформации Грина

Аналогично можно получить в переменных Эйлера:

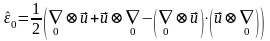
- тензор деформации Альманса.

Если тензоры деформации равны нулю, то расстояния между близкими точками тела не меняются, то есть тело движется как абсолютно твёрдое.

В компонентах разложения по соответствующим базисам приведённые выше формулы имеют вид:

Символ «,i» означает, как обычно, ковариантное дифференцирование по

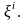
Поскольку при t=0 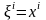то «0,i» соответствует дифференцированию по эйлеровой переменной

.

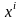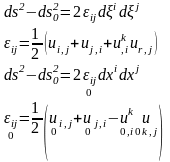
Для твёрдых (упругих, пластических и т.п. – то есть таких, частицы которых не могут свободно перемещаться по внутреннему объёму тела) тел удобнее пользоваться лагранжевыми переменными, в которых естественно задавать граничные условия на их собственных границах этих тел, поскольку образующие их частицы тела при любых непрерывных деформациях остаются всегда на его границах.

Для точки P’₀ с радиус-вектором перемещение можно записать в виде

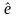Введём симметричную и антисимметричную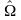 части тензора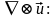

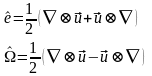
Тогда

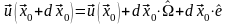
Антисимметричный тензор второго ранга в трехмерном пространстве можно заменить аксиальным вектором

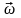
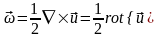
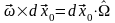
То есть смещение окрестности точки P₀ представляет собой перенос вместе с этой точкой на вектор 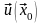поворот вокруг неё как твёрдого целого, определяемый вектором (то есть антисимметричной частью тензора градиента векторного поля деформаций) и объемную деформацию, меняющую расстояния между точками этой окрестности, определяемую тензором 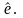Этот вывод называется теорема Коши-Гельмгольца.

Малые деформации

Если деформации малы и все компоненты градиента вектора смещений являются малыми величинами, то выражения для вычисления его симметричной и антисимметричной частей можно упростить, отбросив слагаемые более высокого порядка малости, тогда:

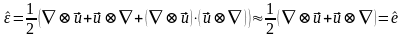
_{В этом случае и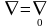} , то есть дифференцирование по совпадает с дифференцированием по 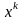поскольку

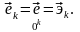
_{ЗАМЕЧАНИЕ. Точное выражение для тензора деформации можно представить в виде}

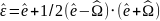
Если растяжения и сдвиги имеют второй порядок малости по отношению к поворотам и смещениям (так деформируются стержни, пластинки и оболочки), то следует считать 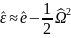(оба слагаемых одного порядка величины).

Тензор деформации симметричен, поэтому его можно привести к главным осям (своим в каждой точке сплошной среды), которые могут быть выбраны взаимноортогональными. В этом собственном ортогональном базисе компоненты тензора деформации образуют диагональную матрицу

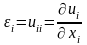
Для обозначения компонентов тензора деформации в произвольной системе координат Теодором фон Карманом были введены названия деформации для диагональных компонентов и сдвиги для половин внедиагональных. В декартовых СК компоненты деформации индексируются одним индексом, соответствующим положению элемента на главной диагонали матрицы 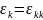(нет суммирования по k!), компоненты сдвигов 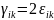. Эти термины используются в литературе по механике сплошных сред. Не следует путать полный тензор деформации, с деформациями по осям координат в смысле Т. Кармана и сдвиги в смысле Т. Кармана с деформацией сдвига (сдвиговой деформацией), которая представляет собой результат равномерного «послойного» смещения слоев сплошной среды!

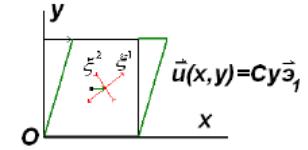
То есть в декартовой системе координат с началом в левом нижнем углу деформируемого квадратного сечения и осями, направленными вдоль его рёбер, смещения вдоль оси OX линейно зависят от ординаты точек среды u_x=Cy, а u_y=0. Компоненты тензора деформаций в этом базисе: 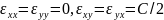. Этому тензору соответствуют собственные векторы

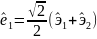
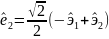. В базисе матрица компонентов тензора деформаций приобретает диагональный вид, соответствующий растяжению по оси 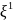и сжатию по оси 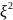: . Псевдовектор поворота при этом движении :

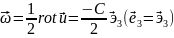Как любой тензор второго ранга, тензор деформации может быть единственным образом представлен в виде суммы шаровой и девиаторной частей:

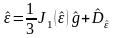, где

В собственном базисе относительное изменение расстояния между близкими точками вдоль каждой оси координат:

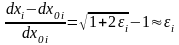
Элемент объёма 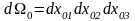после деформации занимает объём

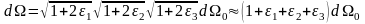
Относительное (по отношению к первоначальному объёму) изменение объёма элемента сплошной среды составит