20

ФЕДЕРАЛЬНОЕ АГЕНТСТВО ПО ОБРАЗОВАНИЮ

ГОСУДАРСТВЕННОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ

ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ

ВЯТСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ

Электротехнический факультет

Кафедра электротехники и электроники

ИССЛЕДОВАНИЕ МАГНИТНЫХ ПОЛЕЙ

ИНДУКТИВНых КАТУШЕК

Методические указания

к лабораторной работе №4

Дисциплина «Теоретические основы электротехники»

Часть 3

Для студентов всех

специальностей ЭТФ и

специальности ЭП

Киров 2010

Печатается по решению редакционно-издательского совета Вятского

государственного университета

УДК 621.3.011.7 (0.76)

Э 45

Составители: Л.М. Агалакова, Г.Г. Гаврилов, А.Л. Козлов, А.А. Красных

Рецензент: кандидат технических наук, доцент Р.В. Хомяков

Подписано в печать Усл.печ.л.

Бумага офсетная Печать матричная

Заказ № Тираж Бесплатно.

Текст напечатан с оригинал-макета, предоставленного авторами

6 10 000, г. Киров, ул. Московская, 36.

Оформление обложки, изготовление – ПРИП ВятГУ

© Вятский государственный университет, 2010

Лабораторная работа №4 исследование магнитных полей катушек индуктивности

4.1. Цель работы

Определение параметров магнитных полей, создаваемых токами, протекающими по индуктивным катушкам.

4.2. Предварительные сведения

4.2.1. Магнитные поля индуктивных катушек

Сведения об основных законах и характеристиках магнитного поля изложены в методических указаниях к лабораторной работе № 3.

В данной лабораторной работе исследуется, как изменяется индукция магнитного поля вдоль оси цилиндрической и кольцевой катушек (рис. 4.1).

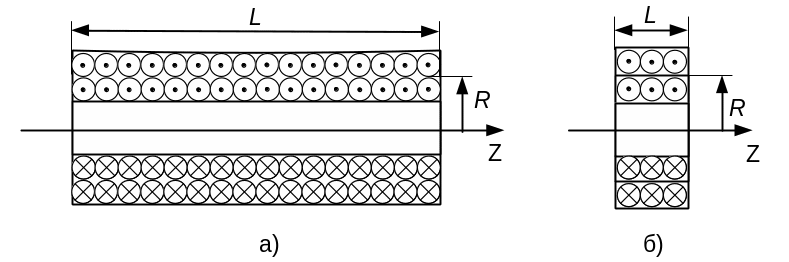
Рис. 4.1. Цилиндрическая (а) и кольцевая (б) индуктивные катушки

Рассмотрим магнитное поле проводника, свернутого в виде спирали. Если длина спирали больше ее диаметра, то такую спираль в физике называют соленоидом (рис. 4.2). Также соленоидом можно назвать индуктивную катушку, намотанную изолированным проводом на цилиндрическую поверхность (рис. 4.1 а).

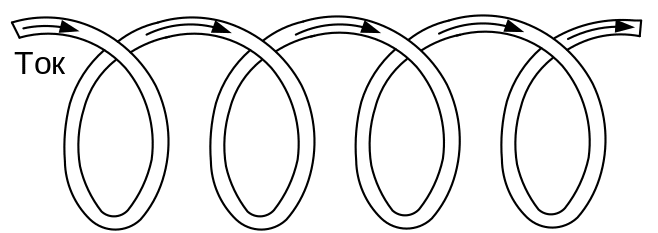
Рис. 4.2. Соленоид

Магнитное поле соленоида создается протекающим по его виткам током. Направление силовых линий магнитного поля определяется по правилу правоходового винта (буравчика).

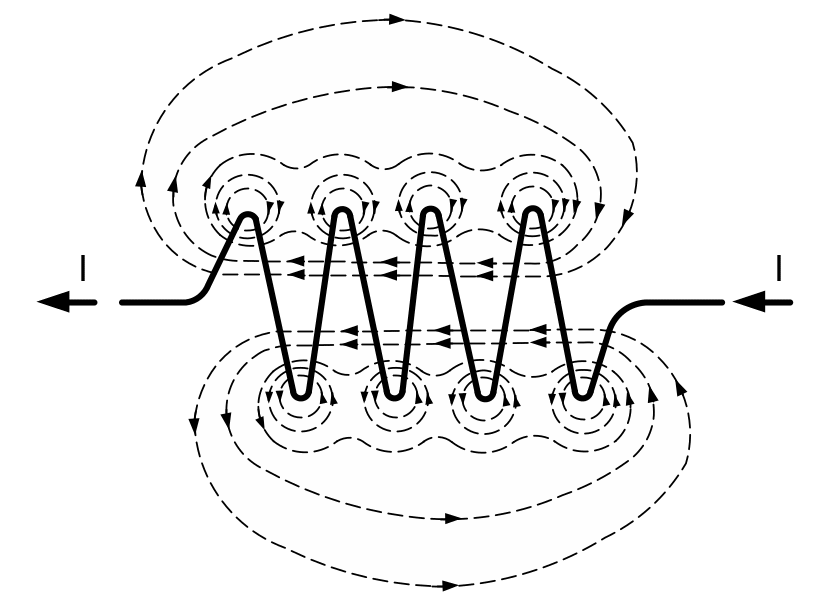
Рис. 4.3. Магнитное поле соленоида

Между каждой парой соседних проводников силовые линии направлены встречно. Это означает, что магнитные поля на данных участках взаимно компенсируются. В результате силовые линии магнитного поля соленоида в целом выходят из одного его конца и входят в другой (рис. 4.4.), то есть соленоид можно рассматривать как магнит.

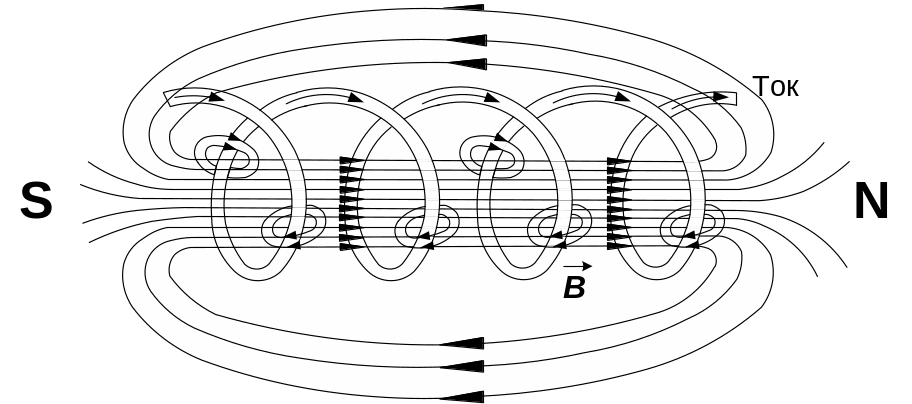
Рис. 4.4. Полюса и силовые линии магнитного поля соленоида (цилиндрической катушки)

Направление поля внутри соленоида и положение полюсов находятся с помощью правила правой руки:

Если наложить на соленоид правую руку с отогнутым большим пальцем так, что бы ток как бы «выходил из пальцев», то отогнутый большой палец укажет северный полюс соленоида.

В средней части внутренней полости соленоида, длина которого значительно больше его диаметра, магнитное поле направлено параллельно оси цилиндра и однородно (рис. 4.4, 4.5). При уменьшении длины соленоида участок с однородным полем внутри его сужается.

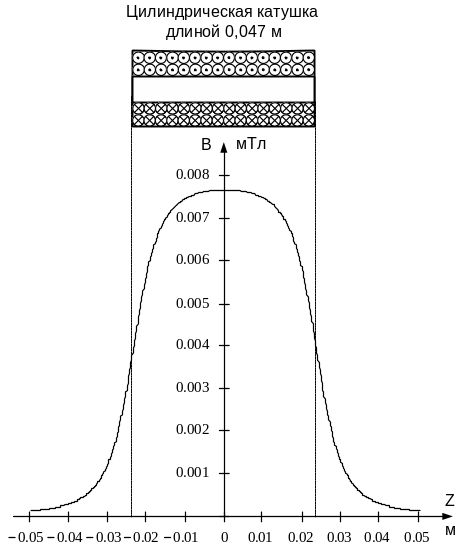
Рис. 4.5. Изменение магнитной индукции на оси цилиндрической катушки

Кольцевая катушка (рис. 4.1б) представляет собой совокупность определенного числа круговых витков, навиваемых на каркас вплотную друг к другу. Ее магнитное поле неоднородно, магнитная индукция имеет ярко выраженный максимум в центре катушки (рис. 4.6).

Если расположить на одной оси две одинаковые кольцевые катушки, соединить их последовательно и согласно, то магнитная индукция (рис. 4.7) на оси катушек будет иметь два максимума в тех местах, где расположен центр каждой катушки.

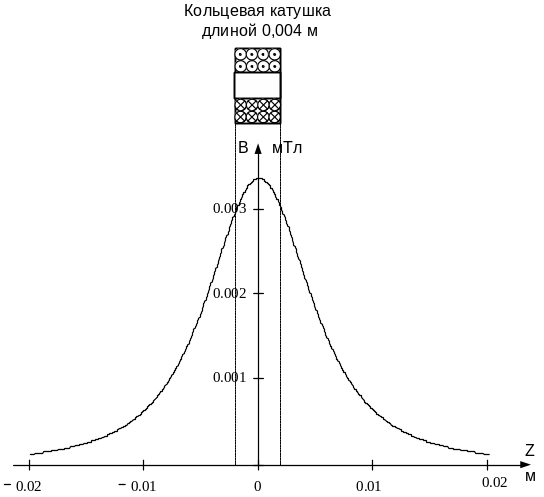
Рис. 4.6. Изменение магнитной индукции на оси кольцевой катушки

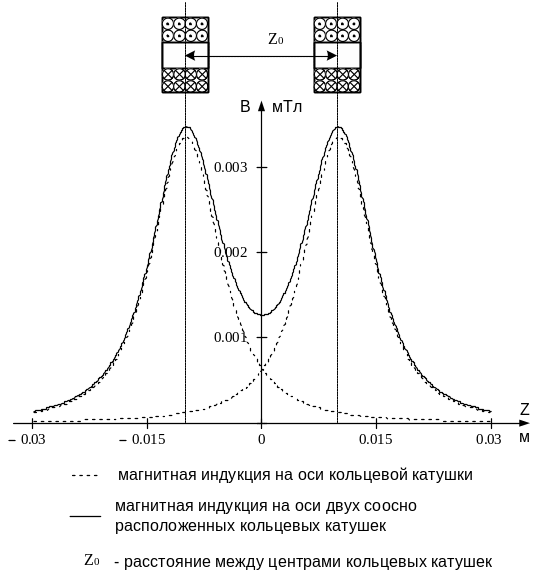
Рис 4.7 Изменение магнитной индукции на оси двух последовательно соединенных соосно расположенных кольцевых катушек (согласное включение)

Одним из законов, используемых при расчетах магнитных полей, в том числе и полей индуктивных катушек, является известный из физики закон Био-Савара-Лапласа. Согласно ему элемент линейного провода (рис. 4.8) с текущим в направлении током I создает в точке М, удаленной на расстояние R от точки А, магнитную индукцию:

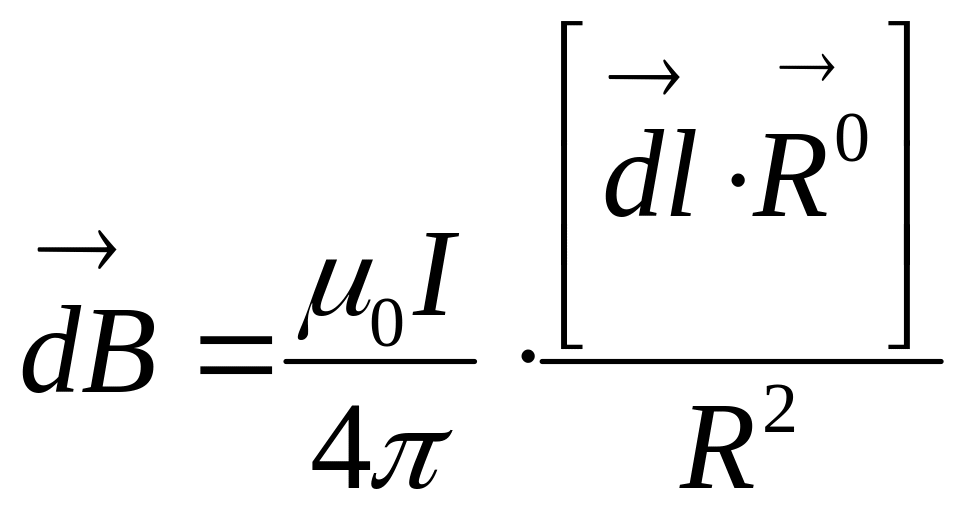, (4.4)

где – единичный вектор, проведенный от точки А к точке М, в которой определяется магнитная индукция.

Рис. 4.8. Ориентация векторов в законе Био-Савара-Лапласа.

Вектор перпендикулярен к плоскости, в которой лежат векторы и , и направлен (согласно определению векторного произведения) так, что совпадает с направлением движения острия правоходового винта, если головку последнего вращать по кратчайшему направлению от к . Такое же направление следует из правила буравчика.

По принципу суперпозиции полей, который справедлив так же для магнитного поля, магнитная индукция в любой точке магнитного поля проводника с током I равна векторной сумме индукций элементарных полей, создаваемых всеми участками проводника.

При , где интегрирование распространяется на всю длину l проводника. Тогда результирующая индукция в точке М:

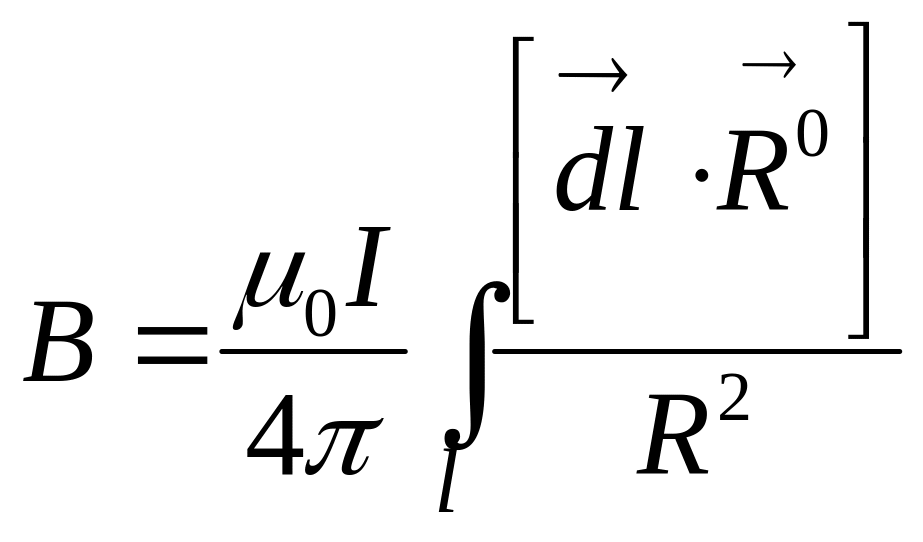. (4.5)

Если сравнивать закон Био-Савара-Лапласа с законом полного тока, то следует отметить, что закон полного тока применим только к замкнутым контурам с токами, тогда как закон Био – Савара – Лапласа применим и к отрезкам проводов с токами (к элементам тока), то есть более универсален.

С помощью закона Био – Савара – Лапласа получены формулы для расчета индукции и напряженности магнитных полей, создаваемых в точках на оси контурами различной конфигурации, в частности, многоугольными рамками, круговым витком (4.6), кольцевой катушкой (4.7), цилиндрической катушкой (4.8).

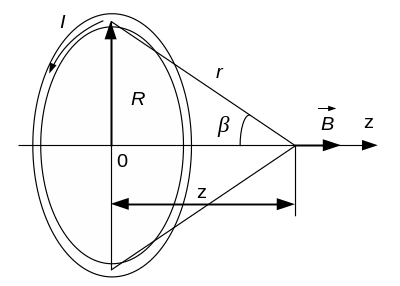
Формула для расчета магнитной индукции в точках на оси кругового витка с током I (рис. 4.9):

, (4.6)

где R – радиус витка;

z – расстояние от центра витка до точки на его оси, в которой определяется значение индукции В.

Рис. 4.9. К расчету магнитной индукции на оси кругового витка	Рис. 4.10. К расчету магнитной индукции на оси цилиндрической катушки

Формула для расчета магнитной индукции в точках на оси кольцевой катушки со средним радиусом R и током I при (при RL):

, (4.7)

где W – количество витков катушки.

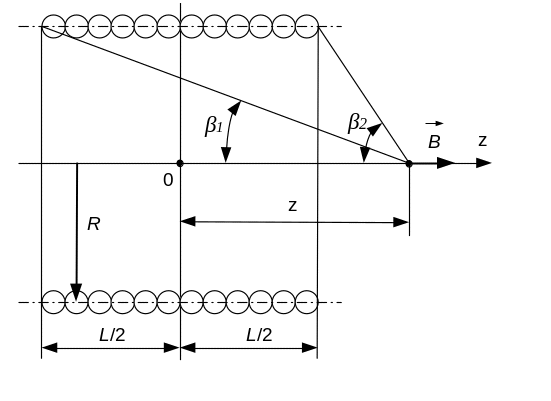
Индукцию в точках на оси однослойной цилиндрической катушки (рис. 4.10) с током I можно рассчитать по формуле:

, (4.8)

где L – длина катушки.

Формулы 4.7 и 4.8 с некоторой погрешностью пригодны и для вычисления магнитной индукции на оси многослойных индуктивных катушек, если толщина обмотки мала по сравнению с радиусом R. При использовании формулы 4.7 для расчета магнитной индукции делается допущение, что длина L кольцевой катушки (рис. 4.1б) по сравнению с радиусом R мала, стремится к нулю. В связи с этим можно считать, что расстояние z₀ между центрами кольцевых катушек (рис. 4.7) практически равно расстоянию между их ближними друг к другу торцами (рис. 4.17).

Следует отметить, что существуют формулы, позволяющие точнее учесть габариты реальных катушек, но они гораздо сложнее формул 4.7, 4.8 и в данной лабораторной работе не используются.

4.2.2. Индуктивность

Возникновение ЭДС индукции в цепи в результате изменения тока в этой цепи называется явлением самоиндукции. Собственное магнитное поле тока в контуре создает магнитный поток Ф сквозь поверхность S, ограниченную самим контуром:

. (4.9)

Магнитный поток Ф называют потоком самоиндукции контура. Если контур находится в неферромагнитной среде или ферромагнитный сердечник незамкнут, то его поток самоиндукции прямопропорционален току i в контуре:

, (4.10)

где L – коэффициент пропорциональности, [Гн]; i – электрический ток;

W – число витков индуктивной катушки;

– потокосцепление индуктивной катушки.

Величину L называют индуктивностью контура. Она численно равна потоку самоиндукции контура при токе 1 А. Индуктивность зависит от геометрической формы контура, его размеров и относительной магнитной проницаемости той среды, в которой он находится.

ЭДС самоиндукции определяется по закону Фарадея:

. (4.11)

Индукционный ток, возникающий вследствие самоиндукции, по правилу Ленца противодействует изменению тока в цепи, замедляя его возрастание или убывание. Индуктивность контура является мерой его инерционности по отношению к изменению тока.

Явление взаимной индукции заключается в наведении ЭДС индукции в проводниках, находящихся вблизи других проводников, токи в которых изменяются с течением времени.

Если две цепи или катушки, например контур 1 и контур 2 (рис. 4.11), расположены друг относительно друга так, что магнитный поток одного из них частично пронизывает и другой, то всякое изменение тока в первой цепи приведет к изменению потока, пронизывающего вторую цепь, и появлению в ней ЭДС взаимоиндукции. И обратно, изменение тока во второй цепи приведет к изменению магнитного потока, связанного с первой цепью, и к возникновению в ней ЭДС взаимоиндукции.

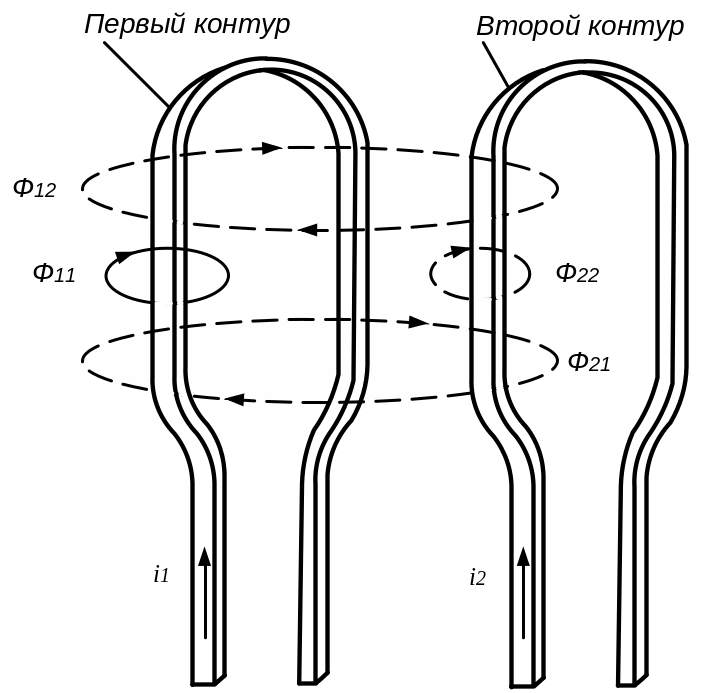
Рис. 4.11. Магнитосвязанные контура

Предположим, что ток i₁ контура 1 создает в контуре 2 магнитный поток Ф₁₂, образующий с витками контура 2 потокосцепление , пропорциональное току i₁. Коэффициент пропорциональности М между потокосцеплением контуров и создавшим его током i₁ называется взаимной индуктивностью контуров 1 и 2 или коэффициентом взаимной индуктивности двух контуров. Он имеет такую же размерность, что и индуктивность:

. (4.12)

Взаимная индуктивность М двух контуров или катушек зависит от числа витков того и другого контура (катушки), их размеров и взаимного расположения, а так же от магнитной проницаемости среды. В неферромагнитной среде, т.е. при постоянной, не зависящей от интенсивности магнитного поля, магнитной проницаемости и неизменном взаимном расположении катушек, их взаимная индуктивность М постоянна и не зависит от тока в той или другой катушке.

Известно, что взаимная индуктивность будет одной и той же независимо от того, связывает ли она потокосцепление контура 2 с создающим его током i₁ в контуре 1, или, наоборот, потокосцепление контура 1 с создающим его током i₂ в контуре 2.

Наведённая ЭДС взаимоиндукции:

, (4.13)

где знак «+» ставят при встречном направлении потоков самоиндукции и взаимоиндукции, а «–» берется при согласном направлении потоков.

Таким образом, взаимную индуктивность можно рассматривать как коэффициент пропорциональности между возникающей ЭДС взаимоиндукции в одной цепи и скоростью изменения тока в другой.

Для определения коэффициента взаимоиндукции М (взаимной индуктивности) контуров или катушек последние следует включить по трансформаторной схеме (рис. 4.12). В первичную цепь включается амперметр, а на зажимы вторичной цепи подключается вольтметр.

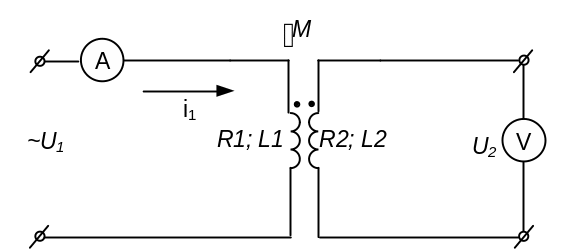
Рис. 4.12. Трансформаторная схема включения магнитосвязаных

контуров

На схеме R1 и R2 – активные сопротивления обмоток взаимодействующих катушек, L1 и L2 – индуктивности взаимодействующих катушек.

Вольтметр будем считать идеальным ( ), поэтому тока во вторичной цепи не будет. В режиме холостого хода во вторичной цепи по закону электромагнитной индукции наводится напряжение

. (4.14)

После перехода к комплексам действующих значений

, (4.15)

где - циклическая частота питающей сети.

Для действующих значений тока и напряжения это будет выглядеть следующим образом:

, (4.16)

следовательно

. (4.17)

При изменении расстояния z между катушками изменяется коэффициент взаимоиндукции M. График M = f(z) изображен на рис. 4.13.

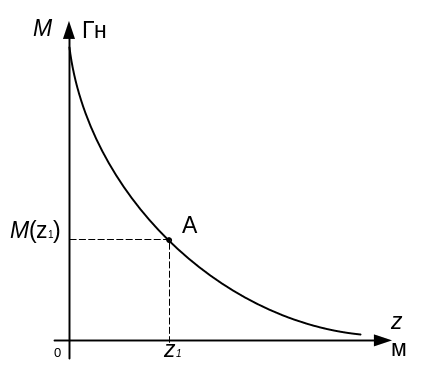
Рис. 4.13. Зависимость взаимной индуктивности М магнитосвязанных контуров от расстояния z между ними