1.4. Максимально-допустимый риск аварии объекта

Обоснованием для назначения максимально-допустимого риска аварии объекта может служить только закон, который характеризует распределение плотности вероятностей риска аварии на неограниченном множестве новых зданий и сооружений. Теоретически, кривая распределения для плотности вероятностей риска аварии существует, но построить её обычными в инженерной практике методами теории вероятностей и математической статистики не представляется возможным из-за полного отсутствия статистических данных о возможных значениях риска аварии. Однако, исходя из физических соображений, на основе нечеткой логики, можно ввести две аксиомы относительно распределения случайной величины r = Р_Ф/Р_Т:

1. Вероятности значений r  1 равны нулю, поскольку обеспечить в процессе строительства теоретическую вероятность аварии Р_Т не удается по целому ряду объективных причин.

2. Кривая распределения случайной величины r является асимметричной, так как из-за естественного стремления общества обеспечить безопасность среды своего обитания значение r с максимальной плотностью вероятности (мода случайной величины) сдвинуто влево от среднего значения.

В [6] для описания случайных величин, принимающих лишь положительные значения, рекомендованы законы, основанные на распределениях Пирсона. Из них принятым выше аксиомам отвечает однопараметрическое распределение Рэлея, имеющее вид: f(r)=(r–1)/² ехр –(r–1)²/2². Также известно [6], что параметр  в распределении Рэлея – это среднеквадратичное отклонение, и связано оно с математическим ожиданием (средним значением) риска аварии R и модой  r  соотношениями: R = 1 + 1,25 ;  r  =  + 1. Этот факт означат, что для полного описания закона распределения случайной величины r достаточно знать значение одной из величин: , R, или  r .

Определить среднее значение риска аварии R на неограниченном множестве новых зданий и сооружений можно. Для этого следует воспользоваться вытекающим из формулы r = 1/ соотношением, связывающим математические ожидания двух случайных величин – риска аварии и показателя  надежности несущего каркаса объекта и имеющим вид: R = 1/М. Численные значения случайной величины  находятся в пределах от 1 до 0. Очевидно, что на том же множестве новых зданий закон ее распределения является симметричным относительно значения  = 0,5. Отсюда следует, что, независимо от вида кривой ее распределения, математическое ожидание случайной величины  будет равно 0,5. Следовательно, среднее значение риска аварии R в естественных условиях (естественный риск аварии объекта), вокруг которого группируются возможные значения случайной величины r, для новых зданий равно числу 2.

По логике, допустимый риск не может быть выше риска в естественных условиях, на который у людей спокойная реакция. Исходя из этой позиции, максимально-допустимый риск аварии построенного здания (сооружения) не должен превышать величины R_макс = 2.

1.5. Пороговые риски аварии и закон деградации объекта

Среднее значение риска аварии в процессе эксплуатации объекта, из-за износа и старения конструкций его несущего каркаса, постепенно увеличивается. При этом растет степень неопределенности технического состояния несущего каркаса, показателем которой служит информационная энтропия закона, характеризующего распределение риска аварии объекта. В общем случае (при любом законе распределения) информационная энтропия определяется по формуле [9]:

Н = – ∑P(A_i )log₂P(A_i), где P(A_i) – вероятность события, определяемая из закона распределения и заключающаяся в том, что риск аварии находится в i-м диапазоне значений.

На рис.2 приведен график функции Н(R), показывающий зависимость информационной энтропии Н от величины математического ожидания R закона распределения риска аварии объекта. Он построен на основе компьютерного эксперимента и его при построении предполагалось, что приведенный выше закон распределения риска аварии, характерный для новых зданий, в процессе эксплуатации объекта не изменяется.

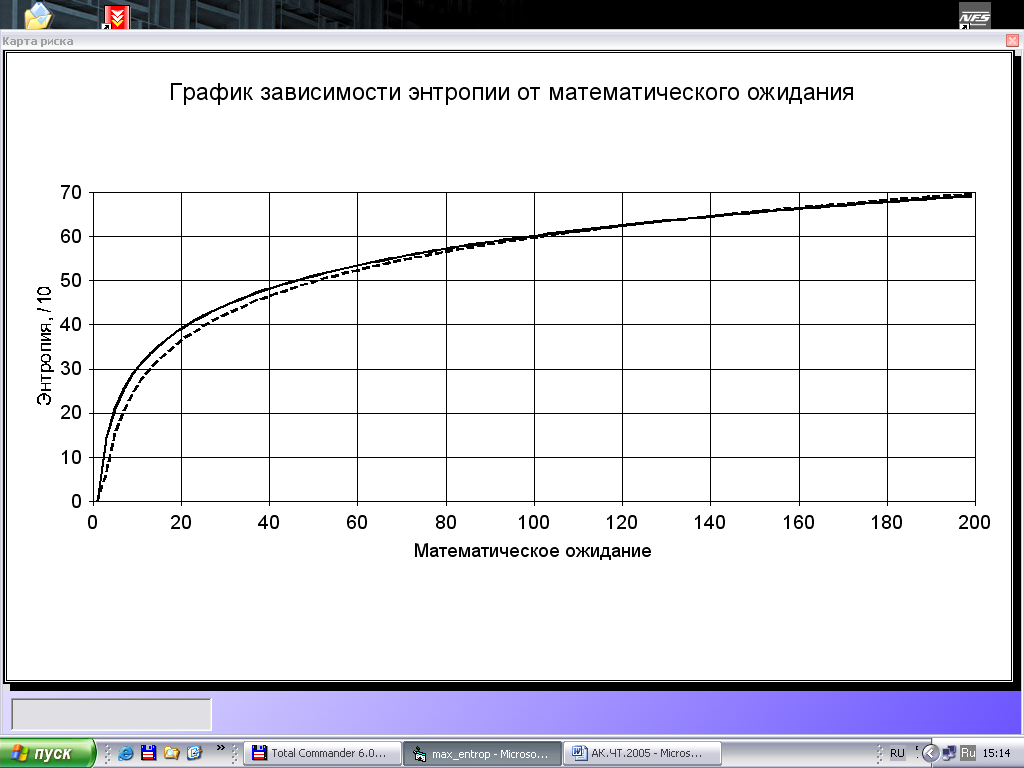
Рис. 2. Зависимость информационной энтропии от величины

среднего риска аварии строительного объекта

Кривая на рис. 2 по существу является законом деградации несущего каркаса строительного объекта. Известно [49], что всякое изменение интенсивности роста скорости энтропии информирует об изменении вида его технического состояния. Для построения графика зависимости скорости и интенсивности скорости роста энтропии от среднего значения риска аварии график на рис. 1 аппроксимирован уравнением Н(R)= log_2,15 ·R (пунктирная линия на рисунке). Полученные по этому уравнению графики зависимости скорости и интенсивности скорости роста энтропии показаны на рис. 3.

Примечание. В исследованиях энтропии участие принимал инж. Косогоров В.Г.

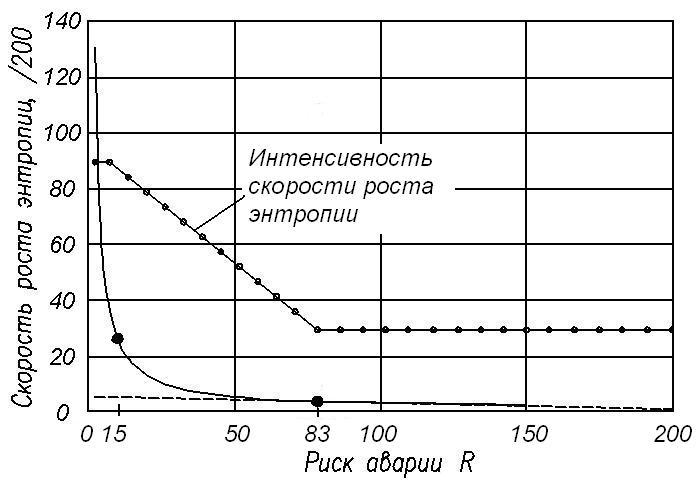
Рис.3 Зависимость скорости и интенсивности скорости роста энтропии

от среднего значения риска аварии объекта.

Из этого рисунка следует, что после значения среднего риска аварии R=15 интенсивность скорости роста энтропии начинает снижаться. Этот факт означает, что объект постепенно переходит из безопасного состояния в состояние аварийное. Интенсивность скорости роста энтропии вновь претерпевает изменение при значении среднего риска, равного 83. После этой величины риска аварии интенсивность скорости роста энтропии вновь становится постоянной. При превышении средним значением риска аварии величины риска, равного 83, объекта начинает переход в ветхо-аварийное состояние. В ветхо-аварийном состоянии равновесие несущего каркаса объекта становится неустойчивым, при котором даже слабые воздействия на объект могут привести к его обрушению. Именно этим подтверждается бытующее в среде строительных экспертов мнение, что дата наступления аварии ветхо-аварийного здания (сооружения) открыта.

По информации этого раздела можно сделать следующие выводы:

1. Существуют пороговые значения риска аварии, при достижении которых строительный объект переходит в качественно иное техническое состояние – из безопасного в аварийное, а из аварийного состояния в ветхо-аварийное.

2. Пороговые значения риска аварии не зависят ни от конструктивного типа здания (сооружения), ни от его этажности, то есть являются инвариантами, что вытекает из способа доказательства их существования.

3. Пороговые значения риска аварии объекта являются неотъемлемой частью закона деградации несущего каркаса здания, представленного на рис.2 в форме диаграммы «энтропия – средний риск аварии».