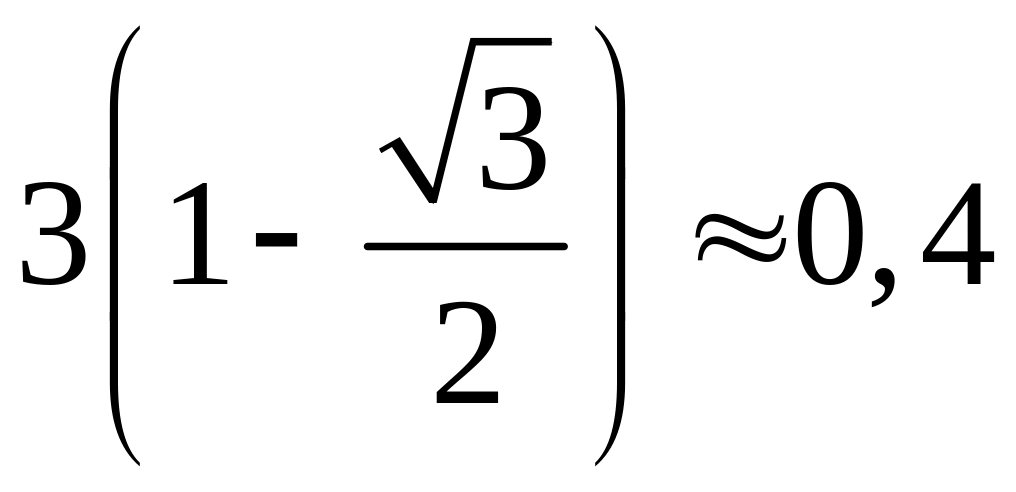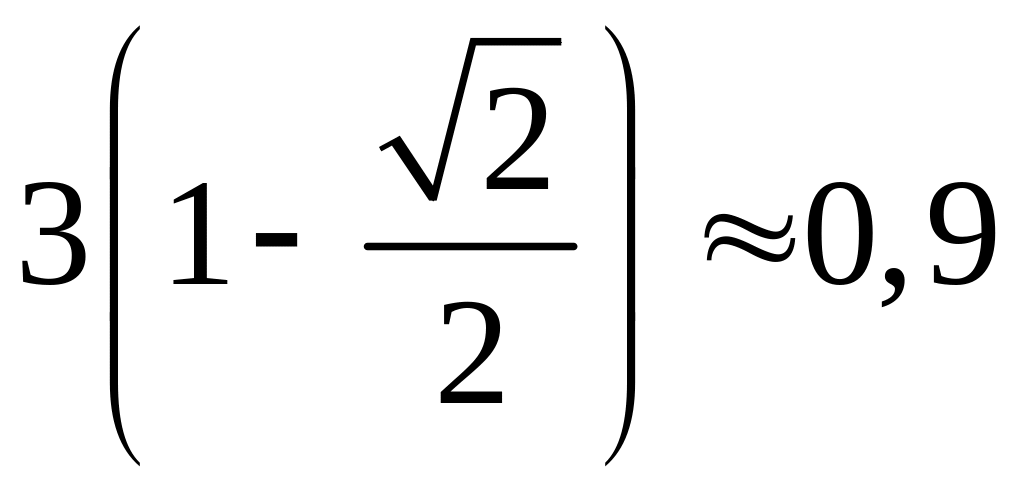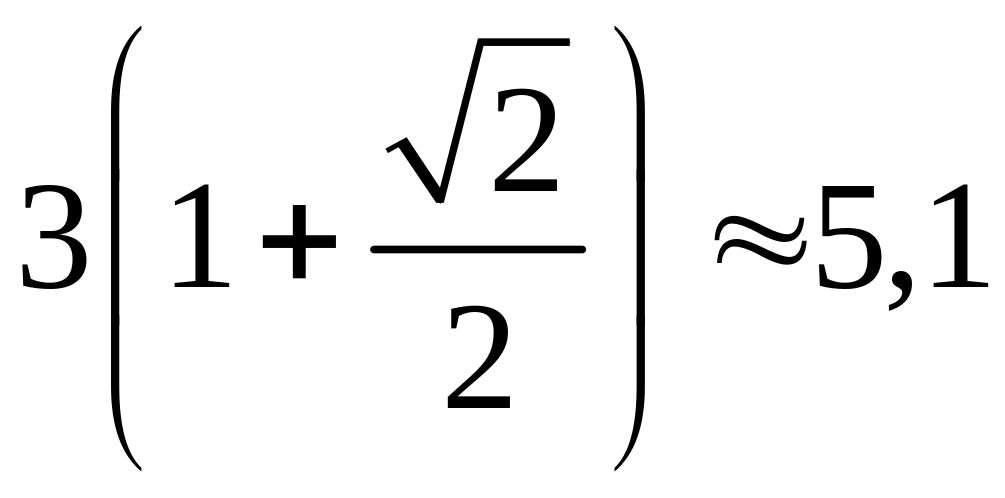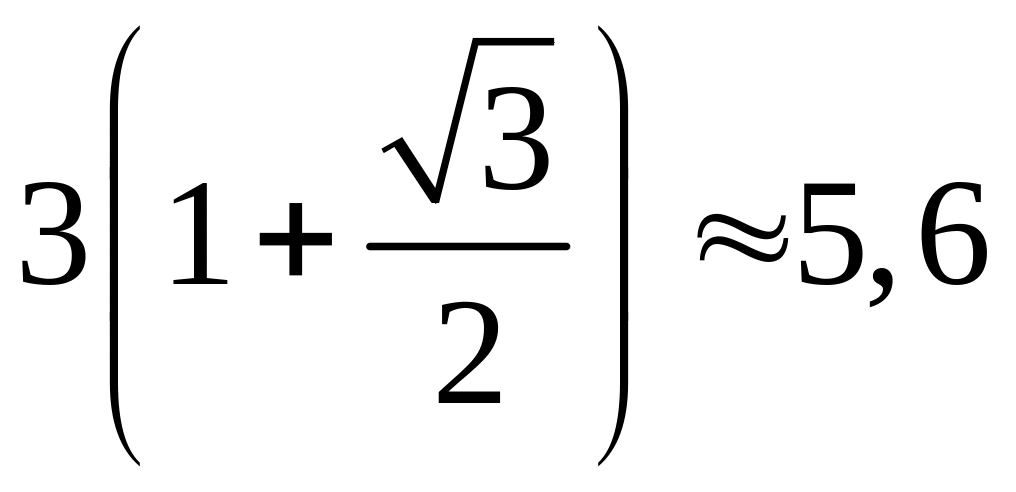3.2. Примеры выполнения заданий типового расчета

Задание 1. Заданы координаты точек в полярной системе координат: : 1) построить точки в ПСК; 2) найти их координаты в ДПСК.

Решение.

1) Сначала надо задать ПСК, используя определение 4 п. 1.2. Для этого:

1. Отмечаем на плоскости точку О – начало координат (полюс).

2. Проводим через точку О луч ОР (полярная ось).

3. От полюса в направлении полярной оси откладываем произвольной длины отрезок – принимаем его за единицу масштаба.

Чтобы изобразить в заданной ПСК точку , проводим через полюс О луч (полуось) под углом к полярной оси ОР (или повернем полярную ось на угол вокруг точки О против часовой стрелки замечание 2, п. 1.2). Затем отложим на полученном луче от точки О в положительном направлении отрезок длины (две единицы выбранного масштаба). Его конец – точка .

Для построения точки надо провести луч под углом к полярной оси ОР (или повернуть полярную ось на угол вокруг точки О по часовой стрелке) и отложить на нем от точки О отрезок длины (три единицы масштаба). Его конец – точка .

Для построения точки нужно провести луч , составляющий с полярной осью угол или, что тоже, и отложить на нем от полюса 3/2 единицы масштаба. Все три заданные точки построены на рис. 10.

2) Выполним вторую часть задания. Найдем прямоугольные декартовы координаты точек. Необходимо воспользоваться формулами (1) п. 1.3. Подставляя вместо координаты точки , получим:

Итак, в ДПСК координаты . Аналогично получим координаты точек (рис.11).

Совместим рис.10 и рис.11 так, чтобы начало координат ДПСК совпало с полюсом ПСК, а направление полярной оси ОР – с направлением оси Ох. Очевидно, что построенные точки совпали.

Задание 2. Заданы координаты точек в ДПСК: . 1) Найти их полярные координаты; 2) построить точки в ПСК и ДПСК, совместив эти системы координат.

Решение.

1) Для нахождения полярных координат заданных точек воспользуемся формулами (2) и (3).

Для точки имеем: , тогда . Так как , то . Таким образом в полярных координатах .

Для точки имеем: , тогда . Так как , то Таким образом в полярных координатах .

Для точки : , . Так как , то . Полярные координаты .

2) Совместим ПСК с ДПСК и построим точки с заданными и полученными координатами. Построение точек в ПСК рассмотрено в задании 1.

Задание 3. Даны уравнения кривых в ПСК . Построить кривую в ПСК и получить её уравнение в ДПСК: а) ; б) ; в) ; г) .

Решение. а) - спираль Архимеда (п. 2.2)

Для построения кривой воспользуемся правилом п. 2.6:

1) Найдем пределы изменения полярного угла, решая неравенство . Тогда

2) Выберем главное значение угла . Поскольку - функция не периодическая, то , с учетом , имеем ;

3) Составим таблицу значений и . Будем придавать значения полярному углу через промежуток (выбран произвольно).

Например, при ,

при ,

при ,

при .

Полученные значения записываем в таблицу:

	0
	0

3. По таблице строим точки с найденными полярными координатами : 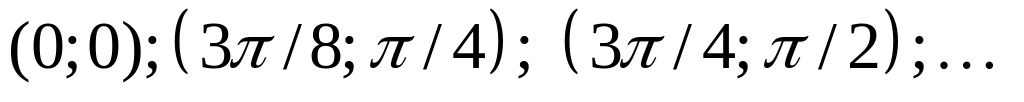Построение точек в ПСК было рассмотрено в задании 1.

4. Соединим построенные точки плавной линией, получим приближенно спираль Архимеда.

Запишем уравнение в ДПСК, используя формулы (2) и (3): .

Б) - окружность со смещенным центром, R = 2 (п.2.1).

Построим её в ПСК , пользуясь правилом п. 2.6.

1. Найдем пределы изменения полярного угла, решая неравенство . Тогда (табл.2)

2. Функция периодическая. Выберем главные значения углов: при n = 0 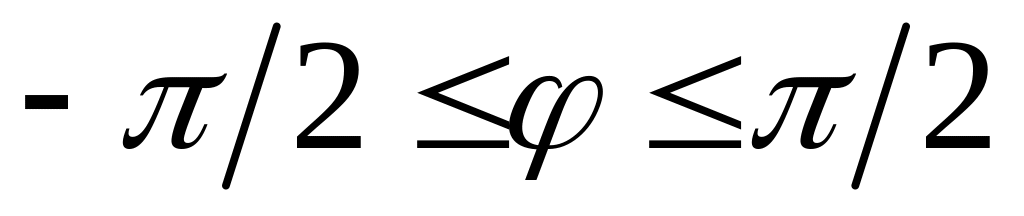(т.е. угол берем в I и IV четвертях). При n = 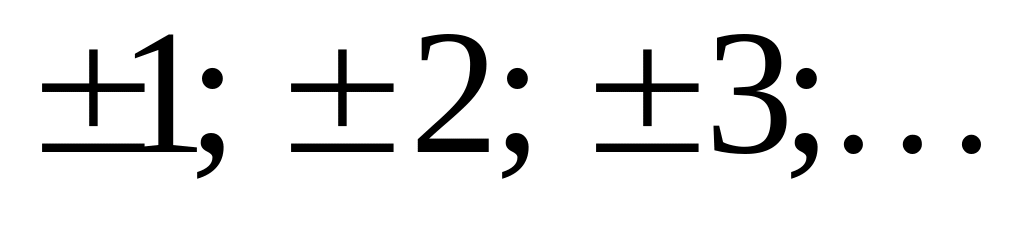значения угла выходят за промежуток 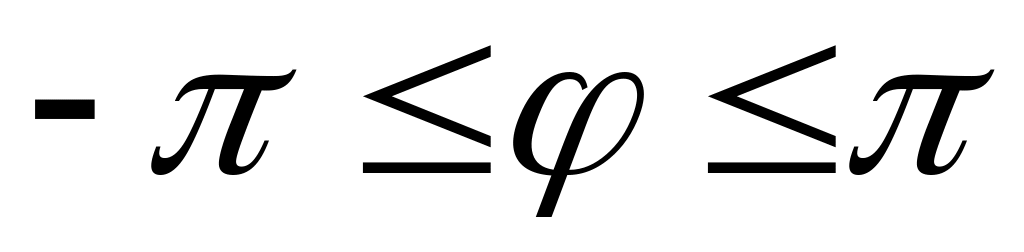или .

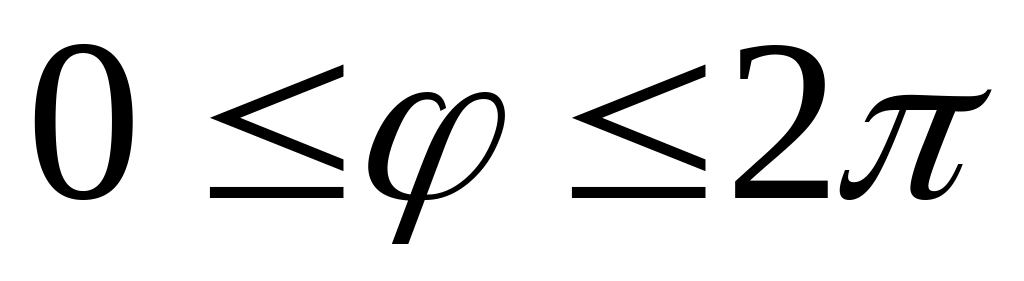3. Составим таблицу значений и .

	0	2			4			2	0

4. Строим точки с найденными координатами

5. Соединим точки плавной линией, получим приближенно окружность радиусом R = 2.

Замечание: построение графика можно провести другим способом. Так как функция четная, т.е. , при построении достаточно ограничиваться значениями , а затем отразить график симметрично относительно полярной оси для углов .

Составим уравнение данной окружности в ДПСК. В силу формул (2) имеем: 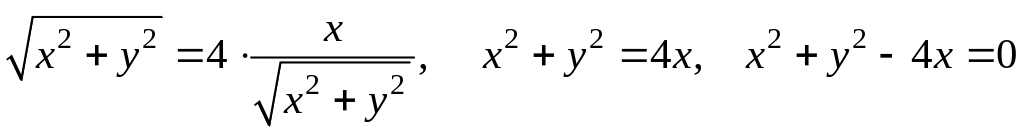. Приведем к каноническому виду: - окружность со смещенным вдоль оси Ох центром (2;0) и радиусом 2.

В) - кардиоида (п. 2.3).

Строим заданную кривую:

1. Найдем пределы изменения полярного угла, решая неравенство . Тогда 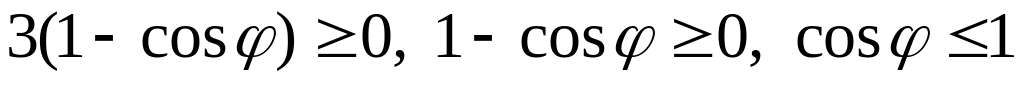. Воспользуемся табл.2.

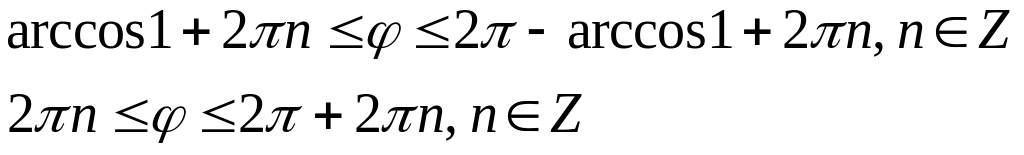
2. Функция периодическая. Выберем главные значения полярных углов, т.е. или . При n = 0 : . При n = значения угла выходят за промежуток .

3. Составим таблицу значений и .

	0
	0			1,5		4,5

		6	4,5	3	1,5			0

При вычислении значений мы пользовались формулами приведения:

.

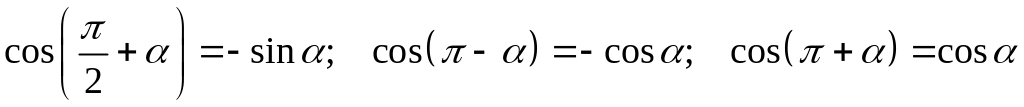Например, ,

,

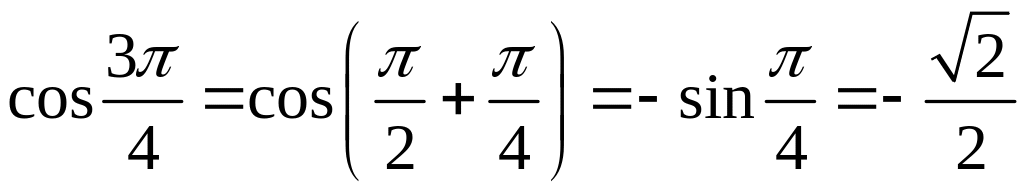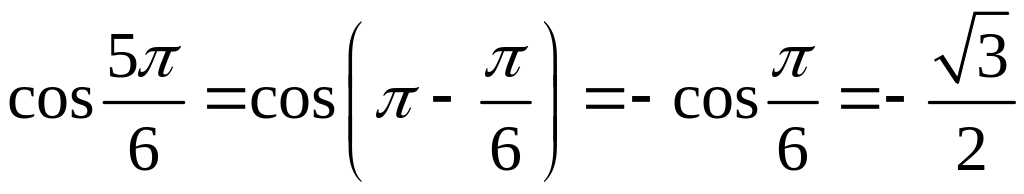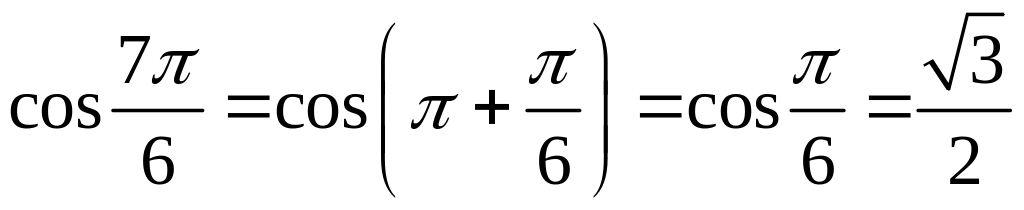и т.д.

Можно вычислять значения на калькуляторе.

4. Строим точки с найденными координатами

5. Соединим точки плавной линией, получим приближенно кардиоиду.

Замечание: построение графика можно провести другим способом. Так как функция четная, т.е. , при построении достаточно ограничиваться значениями , а затем отразить график симметрично относительно полярной оси для углов .

При переходе к ДПСК уравнение кардиоиды примет вид: умножим обе части равенства на , получим или .

Задание 4. Даны уравнения кривых в ДПСК . Получить их уравнения в ПСК и построить в ПСК. А) ; б) .

Решение. а) - это окружность с центром в начале координат и радиусом . В ПСК уравнение примет вид: , т.к. . При любом значении полярного угла полярный радиус постоянный и равен .

Б) - это окружность со смещенным центром. Выделяя квадрат в левой части равенства получим каноническое уравнение: . Координаты центра О(0; -3), радиус R = 3. Формулы (2) позволяют найти уравнение этой окружности в ПСК: . Это уравнение распадается на два: и . Первое уравнение представляет при любом полюс – точку О. Второе уравнение: дает все точки окружности (в том числе полюс), поэтому первое уравнение можно опустить. Строим кривую в ПСК.