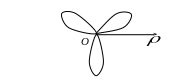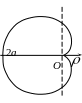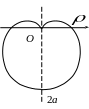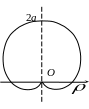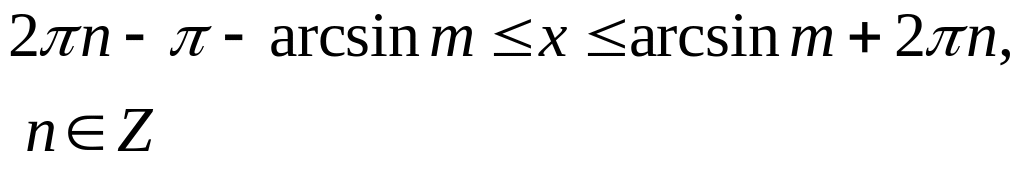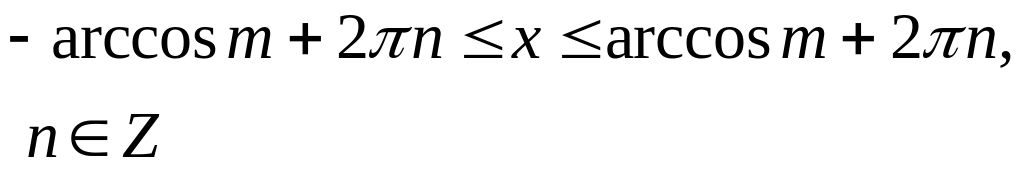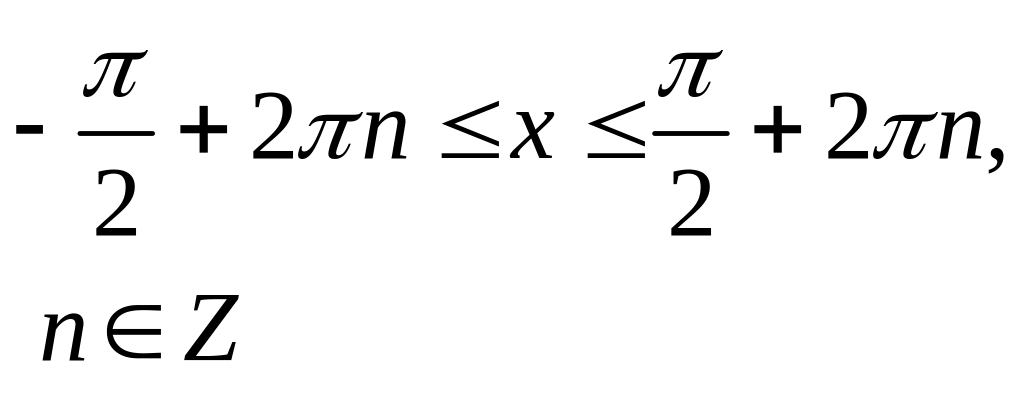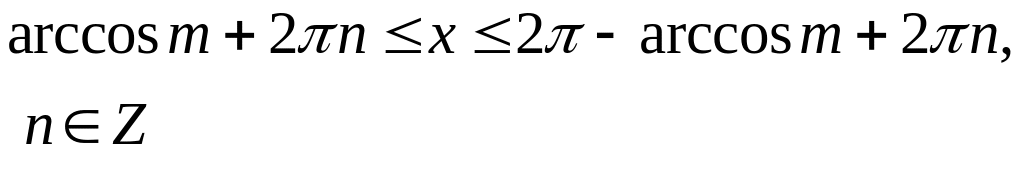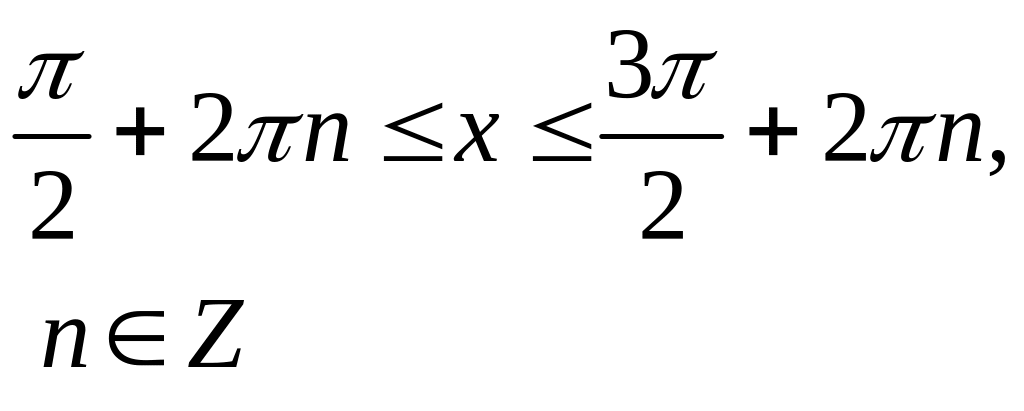- •Полярная система координат
- •1.1. Прямоугольная система координат на плоскости
- •1.2. Полярные координаты точек на плоскости
- •1.3. Связь между прямоугольными декартовыми и полярными координатами точек на плоскости
- •Некоторые линии в полярной системе координат
- •2.1 Окружность
- •2.2 Спираль Архимеда
- •2.3. Розы
- •2.4. Кардиоида
- •2.5. Лемниската Бернулли
- •2.6 Правило построения кривых в полярной системе координат
- •3.1. Варианты типового расчета «Полярная система координат»
- •3.2. Примеры выполнения заданий типового расчета
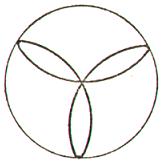
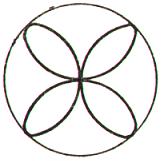
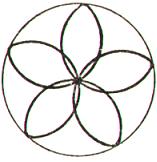
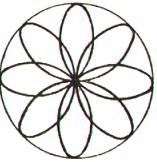
2.3. Розы
О
п р е д е л е н и е 11. Розы – плоские кривые,
уравнения которых в полярных координатах
имеют вид:
![]() ,
где
,
где
![]() и
и
![]() -
постоянные (рис.7).
-
постоянные (рис.7).
|
|
|
|
|
|
|
|
Рис. 7
Вся кривая расположена внутри круга радиуса а, состоит из конгруэнтных лепестков. Если: а) k - нечетное число, роза состоит из k лепестков; б) k -
четное число, роза состоит из 2k лепестков; в) k = m/n, n > 1, - рациональное число, роза состоит из m лепестков когда m и n нечетные и из 2m лепестков, если одно из этих чисел четное (при этом каждый следующий лепесток частично покрывает предыдущий); г) k - иррациональное число, роза состоит из бесчисленного множества лепестков, частично накладывающихся друг на друга.
Т а б л и ц а 2
Расположение розы
Уравнение в ПСК |
Чертеж |
1.
|
|
2.
|
|
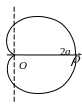
2.4. Кардиоида
О
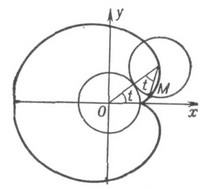 п р е д е л е н и е 12. Кардиоида ( от
греческого
п р е д е л е н и е 12. Кардиоида ( от
греческого![]() - сердце и
- сердце и
![]() -
вид) - плоская алгебраическая кривая
4-го порядка, уравнение в полярных
координатах
-
вид) - плоская алгебраическая кривая
4-го порядка, уравнение в полярных
координатах
![]() .
.
Кардиоида описывается точкой М окружности радиуса а, катящейся по окружности с таким же радиусом. Кардиоида симметрична относительно оси Ох (рис.8).
Рис. 8
Т а б л и ц а 3
Расположение кардиоиды
Уравнение в ПСК |
Схематический чертеж |
Уравнение в ПСК |
Схематический чертеж |
1. |
|
2. |
|
3. |
|
4. |
|
2.5. Лемниската Бернулли
О
п р е д е л е н и е 13. Лемниската Бернулли
(от лат. lemniscatus
- украшенный лентами) – плоская
алгебраическая кривая 4-го порядка,
уравнение в ПСК -
![]() (рис 9).
(рис 9).
П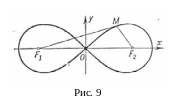 роизведение
расстояний каждой точки М
лемнискаты Бернулли до двух данных
точек
роизведение
расстояний каждой точки М
лемнискаты Бернулли до двух данных
точек![]() и
и
![]() (фокусов) равно квадрату половины
расстояния между
и
.
Кривая симметрична относительно осей
и начала координат. Впервые была
рассмотрена Я. Бернулли (1694).
(фокусов) равно квадрату половины
расстояния между
и
.
Кривая симметрична относительно осей
и начала координат. Впервые была
рассмотрена Я. Бернулли (1694).
Т а б л и ц а 4
Расположение лемнискаты
Уравнение в ДПСК |
Уравнение в ПСК |
Чертеж |
1.
|
|
|
2.
|
|
|
2.6 Правило построения кривых в полярной системе координат
Построение
кривых в ПСК
![]() можно осуществлять по точкам следующим
образом:
можно осуществлять по точкам следующим
образом:
Найти пределы изменения полярного угла, решая неравенство (так как - расстояние, всегда величина положительная). При его решении пользуемся таблицей 3.
Если функция периодическая, то необходимо выбрать главные значения углов, т.е.
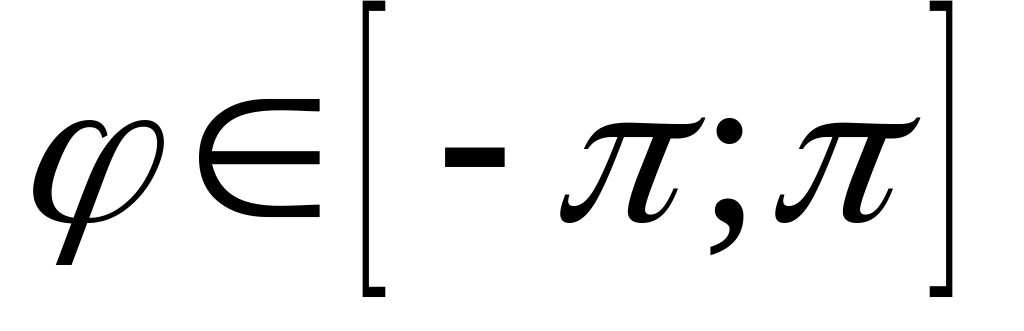 или
или
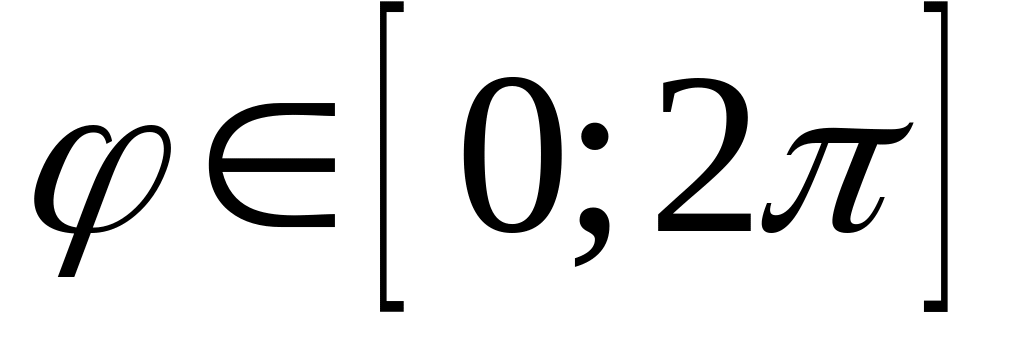 ,
в противном случае
,
в противном случае
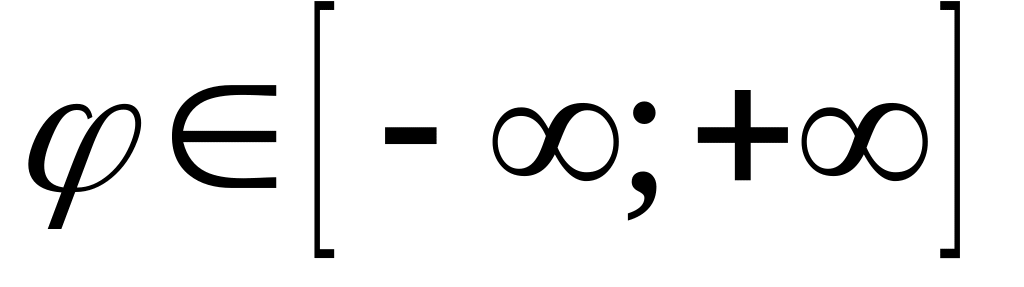 .
.
3.
Составить таблицу значений
и
:
будем давать значения полярному углу
через произвольный промежуток
![]() и
вычислять соответствующее значение
,
подставляя в функцию
.
и
вычислять соответствующее значение
,
подставляя в функцию
.
4.
По таблице построить точки с полученными
координатами
![]() .
.
5. Соединить полученные точки плавной линией. Получили искомую кривую.
Та б л и ц а 5
Решение основных тригонометрических неравенств
Общий случай |
Решение |
Частный случай |
Решение |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ЗАДАНИЯ ДЛЯ САМОСТОЯТЕЛЬНОЙ РАБОТЫ