Лабораторная работа №9. «Изучение линейной корреляционной связи между двумя случайными величинами».
Теоретическая часть.
Задача корреляционного анализа распадается на две:
-установление формы корреляционной связи,
-оценки силы корреляционной связи.
Пусть даны две случайные величины Х и У. Если связь между ними можно считать линейной, то первая задача сводится к отысканию уравнений линейной регрессии
у=ах+b – уравнение регрессии у на х
x=cy+d – уравнение регрессии х на у,
где х и у – средние значения случайных величин, а коэффициенты находятся методом наименьших квадратов.
Решение второй задачи сводится к нахождению выборочного коэффициента линейной корреляции
,
где
– среднее значение произведений
случайных величин Х, У,
,
.
Учитывая, что в работе необходимо не только установление формы связи, но и измерение ее тесноты, уравнение линейной регрессии удобно искать в следующем виде:
,
Решение обеих задач корреляционного анализа осуществляется на ограниченном числе наблюдений, поэтому вычисляемые характеристики отличаются от аналогичных характеристик генеральной совокупности. Возможно, что значение получилось случайно, поэтому необходимо убедиться, что вычисленное значение rв неслучайно.
Проверка этой
гипотезы осуществляется по t-критерию.
Сравнивается наблюдаемое значение
с критическим значением, взятым из
таблицы.
Если n – велико, то tкр находят с помощью функции Лапласа, если n<100, то используют таблицу распределения критических точек Стьюдента.
Если
,
то величины действительно связаны
линейной зависимостью.
Для случаев, когда зависимость между случайными величинами нелинейная по переменным, оценка параметров уравнений регрессии осуществляется тем же методом наименьших квадратов. Простейшие нелинейные формы, которые могут быть использованы, таковы:
,
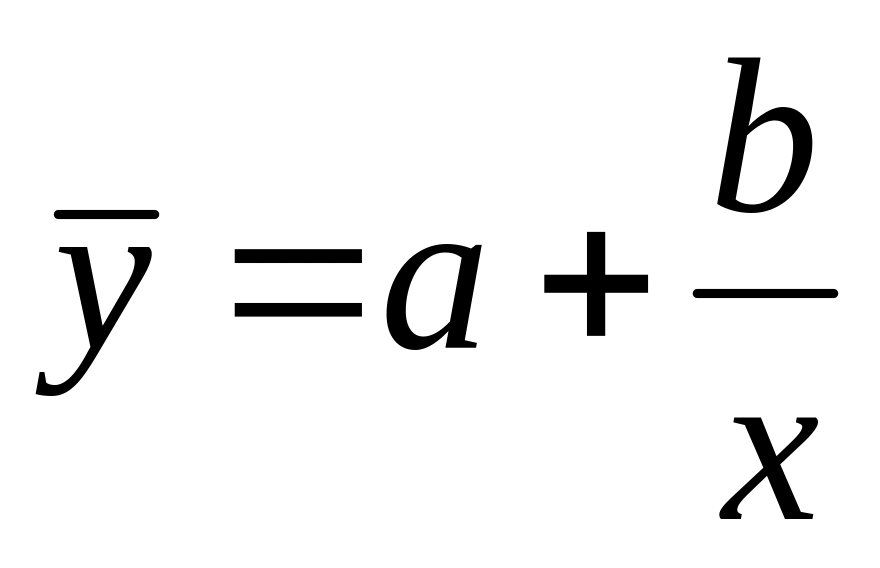чтобы перейти к линейному уравнению,
необходимо положить
.
,
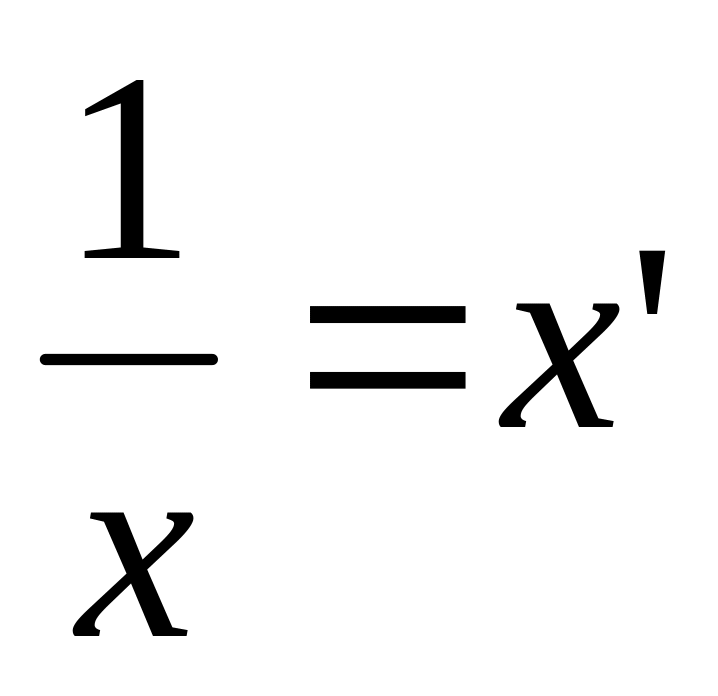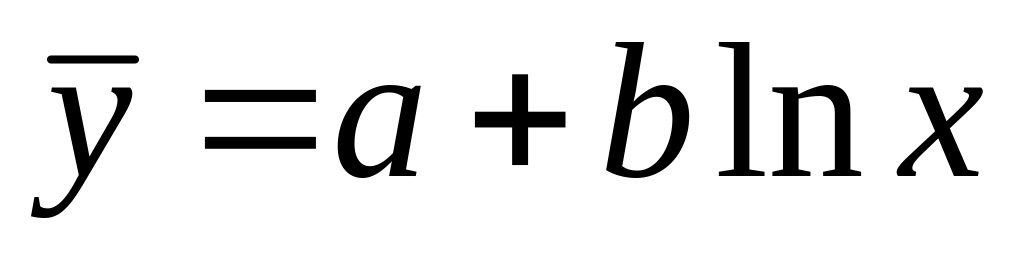полагаем
.
,
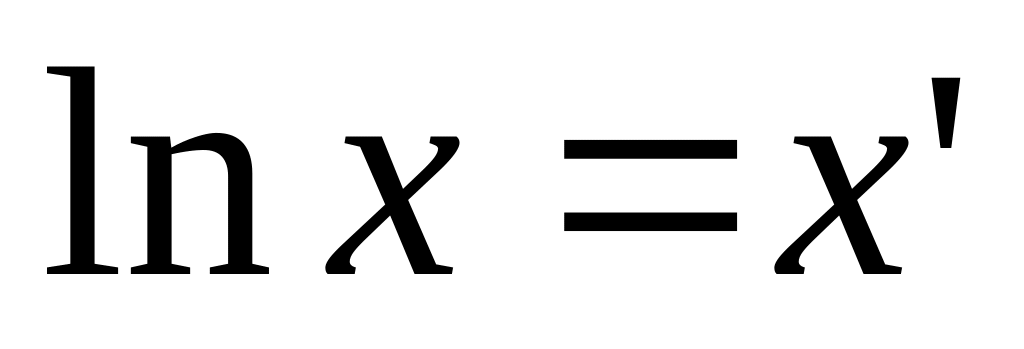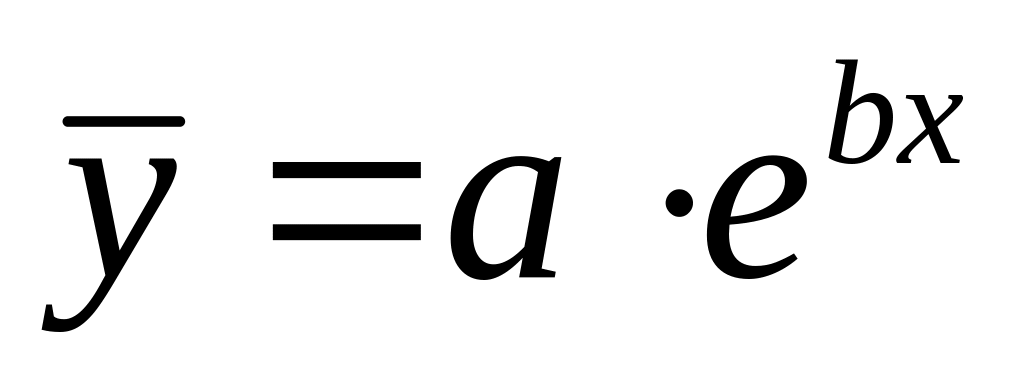прологарифмировав обе части делаем
замены
,
.
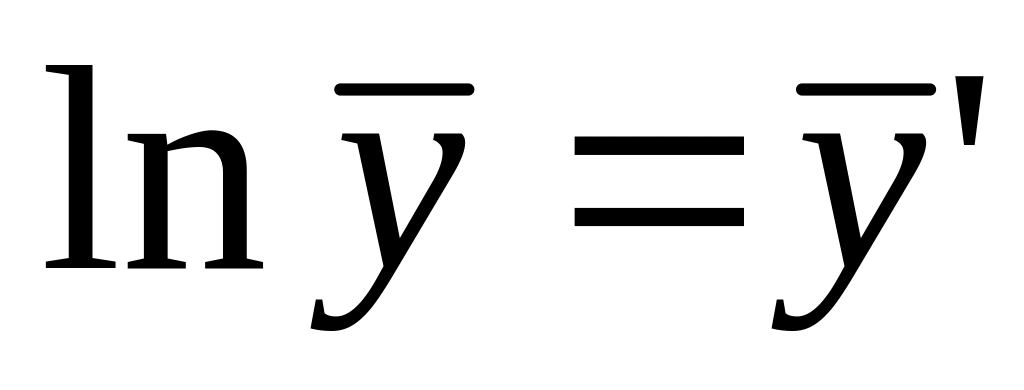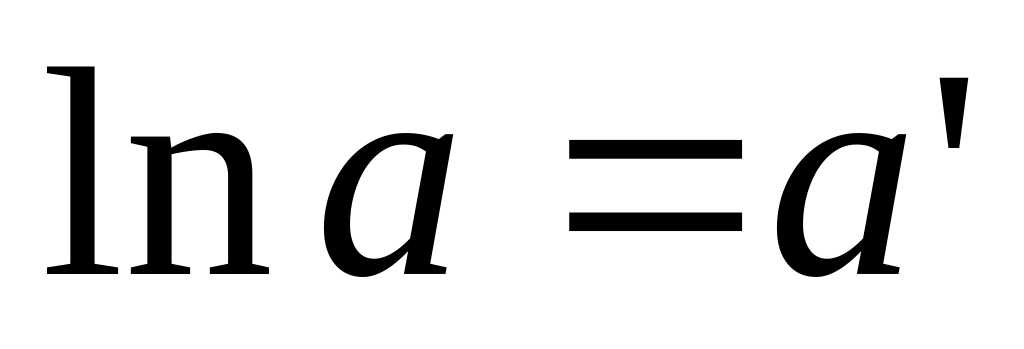Теоретические вопросы.
Что понимается под корреляционной зависимостью.
Дайте определение коэффициента линейной корреляции генеральной совокупности.
Чем отличается корреляционный анализ от регрессионного.
На основе какого метода находятся параметры уравнения линейной регрессии.
Какой содержательный смысл имеет коэффициент линейной регрессии
Какой содержательный смысл имеет свободный член уравнения линейной регрессии.
Задание №1. По исходным данным построить точечную диаграмму. Вычислить коэффициент корреляции, определить силу и направление связи. Подсчитать возможную ошибку и установить значимость коэффициента линейной корреляции.
Варианты к лабораторной работе №9:
Вариант №1.
у х |
5 |
10 |
15 |
20 |
25 |
30 |
35 |
40 |
итого |
100 |
2 |
1 |
- |
- |
- |
- |
- |
- |
3 |
120 |
3 |
4 |
3 |
- |
- |
- |
- |
- |
10 |
140 |
- |
- |
5 |
10 |
8 |
- |
- |
- |
23 |
160 |
- |
- |
- |
1 |
- |
6 |
1 |
1 |
9 |
180 |
- |
- |
- |
- |
- |
- |
4 |
1 |
5 |
итого |
5 |
5 |
8 |
11 |
8 |
6 |
5 |
2 |
50 |
Вариант №2.
у х |
18 |
23 |
28 |
33 |
38 |
43 |
48 |
итого |
125 |
- |
1 |
- |
- |
- |
- |
- |
1 |
150 |
1 |
2 |
5 |
- |
- |
- |
- |
8 |
175 |
- |
3 |
2 |
12 |
- |
- |
- |
17 |
200 |
- |
- |
1 |
8 |
7 |
- |
- |
16 |
225 |
- |
- |
- |
- |
3 |
3 |
- |
6 |
250 |
- |
- |
- |
- |
- |
1 |
1 |
2 |
итого |
1 |
6 |
8 |
20 |
10 |
4 |
1 |
50 |
Вариант №3.
у х |
5 |
10 |
15 |
20 |
25 |
30 |
35 |
итого |
100 |
- |
- |
- |
- |
- |
6 |
1 |
7 |
120 |
- |
- |
- |
- |
- |
4 |
2 |
6 |
140 |
- |
- |
8 |
10 |
5 |
- |
- |
23 |
160 |
3 |
4 |
3 |
- |
- |
- |
- |
10 |
180 |
2 |
1 |
- |
1 |
- |
- |
- |
4 |
итого |
5 |
5 |
11 |
11 |
5 |
10 |
3 |
50 |
Вариант №4.
у х |
6 |
8 |
10 |
12 |
14 |
итого |
30 |
2 |
17 |
9 |
3 |
- |
31 |
35 |
- |
10 |
17 |
9 |
- |
36 |
40 |
- |
3 |
24 |
16 |
13 |
56 |
45 |
- |
- |
6 |
24 |
12 |
42 |
50 |
- |
- |
2 |
11 |
22 |
35 |
итого |
2 |
30 |
58 |
63 |
47 |
200 |
Вариант №5.
у х |
20 |
30 |
40 |
80 |
60 |
итого |
15 |
7 |
5 |
- |
- |
- |
12 |
25 |
20 |
23 |
- |
- |
- |
43 |
35 |
- |
30 |
47 |
2 |
- |
79 |
45 |
- |
10 |
11 |
20 |
6 |
47 |
55 |
- |
- |
9 |
7 |
3 |
19 |
итого |
27 |
68 |
67 |
29 |
9 |
200 |
Вариант №6.
у х |
15 |
20 |
25 |
30 |
36 |
итого |
40 |
5 |
7 |
- |
- |
- |
12 |
50 |
- |
4 |
16 |
23 |
- |
43 |
60 |
- |
8 |
20 |
32 |
27 |
87 |
70 |
- |
- |
11 |
29 |
2 |
42 |
80 |
- |
- |
- |
9 |
7 |
16 |
итого |
5 |
19 |
47 |
93 |
36 |
200 |
Вариант №7.
у х |
2 |
2.5 |
3 |
3.5 |
4 |
итого |
1000 |
- |
- |
- |
2 |
3 |
5 |
2000 |
- |
- |
3 |
6 |
2 |
11 |
3000 |
- |
4 |
6 |
3 |
- |
13 |
4000 |
1 |
6 |
4 |
1 |
- |
12 |
5000 |
6 |
3 |
- |
- |
- |
9 |
итого |
7 |
13 |
13 |
12 |
5 |
50 |
Вариант №8.
у х |
1.25 |
1.5 |
1.75 |
2 |
2.25 |
итого |
8 |
- |
- |
1 |
2 |
3 |
6 |
13 |
- |
- |
1 |
4 |
3 |
8 |
18 |
- |
4 |
7 |
1 |
- |
12 |
23 |
2 |
7 |
5 |
- |
- |
14 |
28 |
6 |
4 |
- |
- |
- |
10 |
Итого |
8 |
15 |
14 |
7 |
6 |
50 |
Вариант №9.
у х |
5 |
10 |
15 |
20 |
25 |
30 |
итого |
10 |
3 |
3 |
- |
- |
- |
- |
6 |
20 |
- |
4 |
4 |
- |
- |
- |
8 |
30 |
- |
- |
7 |
35 |
8 |
- |
50 |
40 |
- |
- |
2 |
10 |
8 |
- |
20 |
50 |
- |
2 |
- |
5 |
6 |
3 |
16 |
итого |
3 |
9 |
13 |
50 |
22 |
3 |
100 |
Вариант №10.
у х |
10 |
15 |
20 |
25 |
30 |
35 |
итого |
50 |
2 |
2 |
- |
- |
- |
- |
4 |
60 |
2 |
4 |
5 |
6 |
4 |
- |
21 |
70 |
- |
2 |
7 |
12 |
10 |
4 |
35 |
80 |
- |
- |
- |
10 |
10 |
6 |
26 |
90 |
- |
- |
- |
8 |
- |
6 |
14 |
итого |
4 |
8 |
12 |
36 |
24 |
16 |
100 |