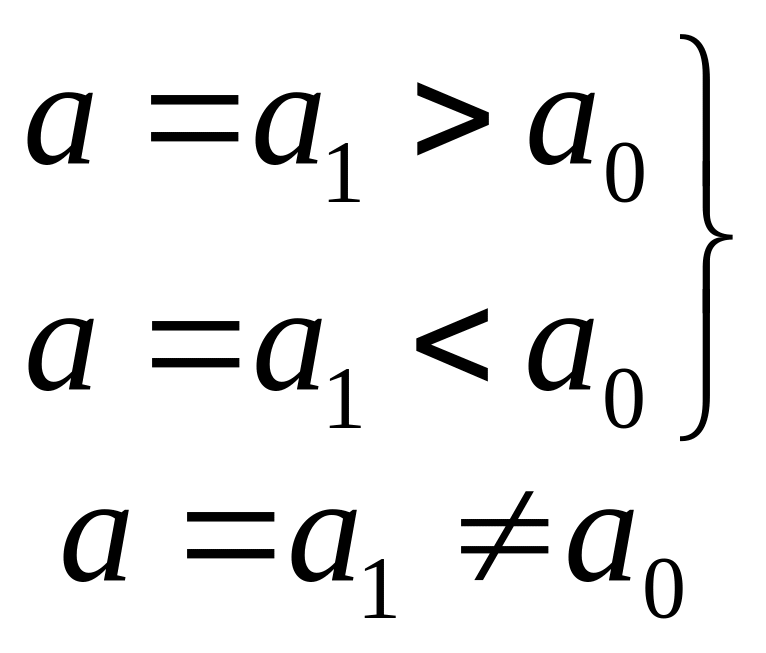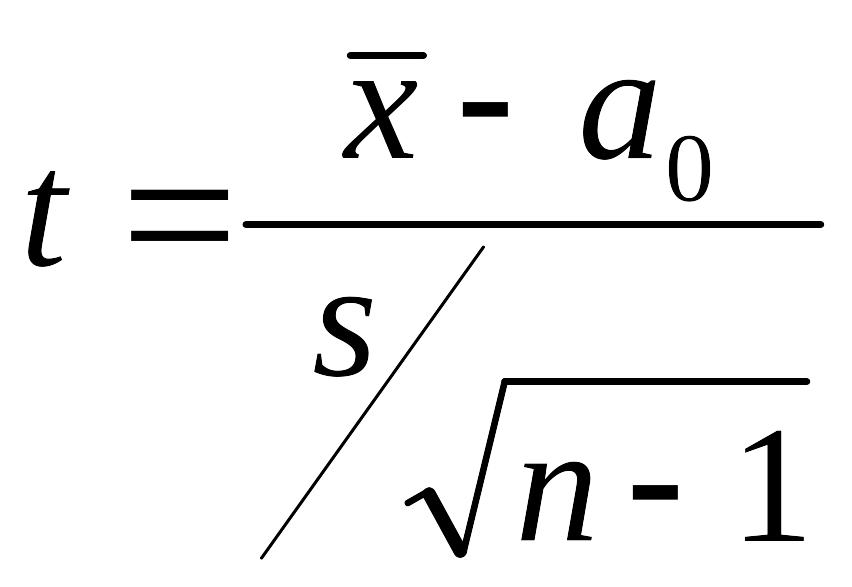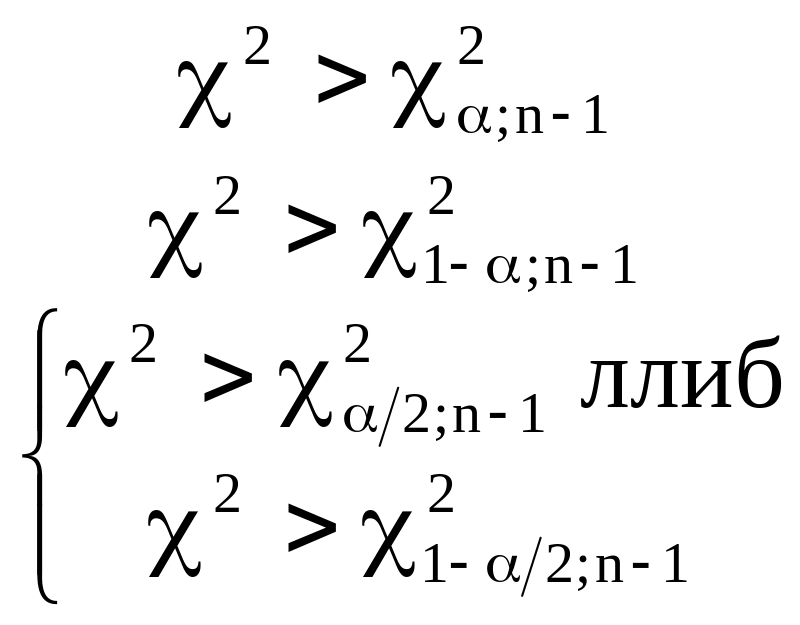Лабораторная работа №8. «Проверка гипотезы о нормальном законе распределения».

Теоретическая часть.

Гипотеза о числовых значениях.

Задача проверки гипотезы о числовых значениях возникает, когда необходимо убедиться в том, что отклонение среднего значения параметра будет соответствовать номиналу, то есть проверить гипотезу Н₀: , против альтернативной Н₁: , или Н₂: . Может возникнуть необходимость проверки гипотезы, что дисперсия равна заданной величине, или доля бракованных изделий равна некоторой заданной величине.

Соответствующие критерии приведены в таблице:

Нулевая гипотеза	Предположения	Статистика критерия	Альтернативная гипотеза	Критерий отклонения гипотезы
а =а0	σ2 известна
	σ2 неизвестна
σ2 =σ02	а неизвестно
р =р0	n большое

Замечание: Критические значения статистик на уровне значимости α определяют по соответствующим таблицам приложений исходя из соотношений:

Суть проверки гипотезы о нормальном распределении состоит в сравнении эмпирических данных о случайной величине с теоретическими. Эта проверка осуществляется с помощью некоторой критериальной величины U. U можно найти по формуле на основе эмпирических данных U_набл и по специальной таблице U_табл. Если гипотеза о выбранном распределении верна, то значение U_набл не должно превышать ее теоретического значения U_табл.

Критерий Пирсона.

Наиболее часто встречаемым на практике является критерий χ²-Пирсона: статистика

или имеет χ²-распределение с k=m-r-1 степенями свободы, где m –число интервалов эмпирического распределения, r- число параметров теоретического распределения, n_i и np_i- соответственно эмпирические и теоретические частоты.

Для расчета теоретических вероятностей используем

при гипотезе о нормальном распределении - функцию Лапласа: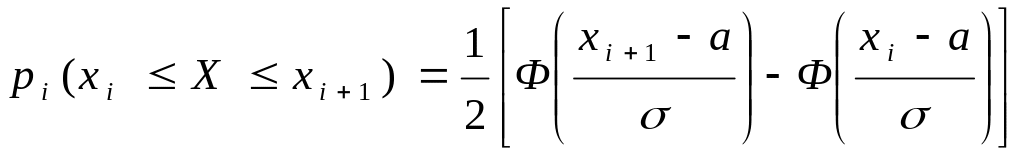 , r =2,

при гипотезе для распределения Пуассона ,где - выборочная средняя, r =1.

Критерий Колмогорова.

В данном критерии в качестве меры расхождения между теоретическим и эмпирическим распределениями рассматривают

, критериальной является величина , которая сравнивается с табличной.

Замечания:

1. Если в некотором интервале количество наблюдений меньше 5 имеет смысл объединить соседние интервалы.

2. Если при применении критерия Колмогорова использовать вместо значений параметров их оценки, то получим большее критическое значение , то есть вероятность принять нулевую гипотезу как правдоподобную, когда она на самом деле противоречит опытным данным.

Теоретические вопросы.

1. Какая гипотеза называется статистической, конкурирующей.

1. В чем заключаются ошибки первого и второго рода.

2. Как влияет изменение уровня значимости на критическую область.

3. Сформулировать схему проверки гипотезы согласно критерию Пирсона.

4. Сформулировать схему проверки гипотезы согласно критерию Пирсона

5. В чем суть критериев согласия, как выбирают критериальную величину.

6. Какие критерии согласия вы знаете.

Практическая часть.

Задание №1. Снять две выборки объемов N₁<<N₂ при заданных математическом ожидании и дисперсии.

Найти для каждой выборки точечные оценки .

Проверить гипотезу Н₀: , против альтернативных Н₁: , Н₂: , Н₃: .

Поверить гипотезу Н₀: , против альтернативных Н₁: , Н₂: , Н₃: ,

Задание №2. Случайным образом сформировать распределение, подчиненное нормальному закону. Проверить гипотезу о нормальном распределении и распределении Пуассона на двух различных уровнях значимости с помощью критериев Пирсона и Колмогорова.

Задание №3. Случайным образом сформировать распределение, подчиненное закону Пуассона. Проверить гипотезу о нормальном распределении и распределении Пуассона на двух различных уровнях значимости с помощью критериев Пирсона и Колмогорова.