Семейство прямых

Применим понятие характеристик к изучению уравнений в частных производных (УЧП) 1-го порядка вида

(18)

Определение 3. Характеристиками УЧП называются характеристики оператора .

Теорема. Если функция удовлетворяет уравнению (18), то есть то на каждой характеристике

Действительно, принимая во внимание (18), вдоль каждой характеристики имеем

Итак,

Отсюда следует, что на каждой характеристике

Физическая интерпретация этого факта

Если - время, то начальное состояние распространяется по характеристикам. Чтобы найти в произвольной фиксированной точке , надо через эту точку провести характеристику, найти ее точку пересечения с осью . Пусть это будет точка тогда . (рисунок 6)

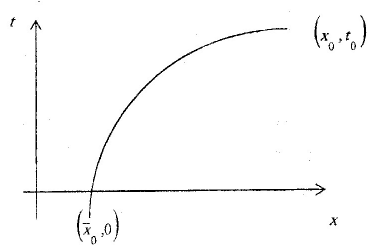
Рисунок 7

Пример 2. На рисунке 6 вдоль каждой характеристики – прямой функция При этом имеет разные значения вдоль различных характеристик, то есть или

Пример 3. Найдем характеристики УЧП 1-го порядка

Дифференциальное уравнение характеристик имеет вид

Разделяя переменные и интегрируя ОДУ получим

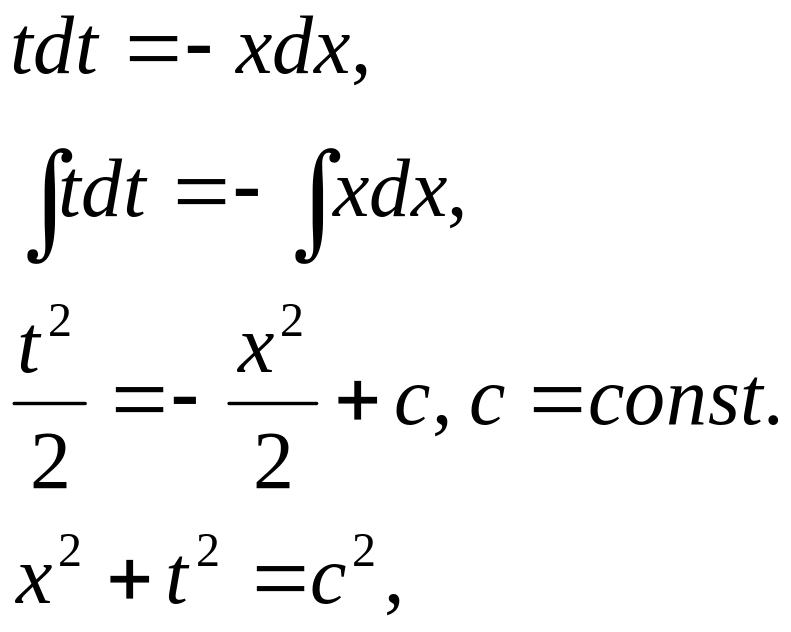
Следовательно, характеристики УЧП представляют собой однопараметрическое семейство окружностей, радиуса , заполняющих собой всю плоскость .

4. Задача Коши. Метод характеристик

Задача Коши состоит в отыскании решения УЧП, если известно начальное отклонение .

Рассмотрим задачу Коши для уравнения переноса

(19)

с начальным условием

(20)

Дифференциальное уравнение характеристик имеет вид

интегрируя его, получаем

Вдоль каждой характеристики - произвольная дифференцируемая функция.

Учитывая начальное условие (20), записываем решение задачи Коши (19)-(20):

Физическая интерпретация полученного решения

Функция называется отклонением в точке в момент времени . Рассмотрим точку . Допустим, далее, что из этой точки в положительном направлении оси в момент времени начинает двигаться наблюдатель со скоростью V. В момент времени он окажется в точке . Величина отклонения, которую наблюдатель будет видеть в точке в момент времени , будет равна Таким образом, наблюдатель в любой момент времени будет видеть в точке, где он находится, одну и ту же величину отклонения, равную . Следовательно, начальный профиль будет двигаться со скоростью в положительном направлении оси , как жесткая система, не изменяя формы (рис.8).

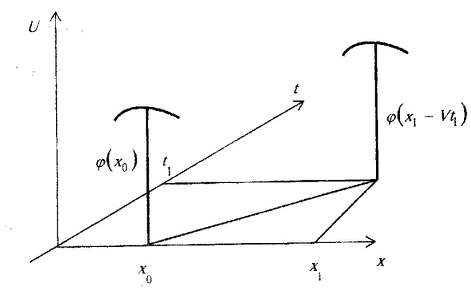
Рисунок 8

Пример 4. Решение задачи Коши для уравнения переноса (6) с начальным условием

имеет вид

.

Пример 5. Уравнение химической кинетики

где

а) привести к виду

б) решить задачу Коши при начальном

а) Выполним подстановку вида

где

в данное УЧП.

Так как

то

Домножив почленно на обе части последнего уравнения, получим

б) Решение полученного УЧП вдоль каждой характеристики это произвольная дифференцируемая функция

Из начального условия

и подстановки

следует

Таким образом, решение промежуточной задачи Коши:

имеет вид:

И, наконец, решение задачи Коши для исходного УЧП:

следует из полученной формулы выполнением подстановки

Пример 6. Решить задачу Коши для УЧП 1-го порядка из примера 3:

Вдоль каждой характеристики данного УЧП- окружности решение этого УЧП – произвольная дифференцируемая функция . Исходя из заданного вида начального профиля получаем следующее отклонение в точке в момент времени :