2. Классификация учп первого порядка

Квазилинейными уравнениями с частными производными первого порядка называются уравнения вида:

где - известные функции,

- функция, подлежащая определению.

Если функции от не зависят, то уравнение с частными производными называется линейным; если функция то УЧП называется однородным.

Типология учп первого порядка

Таблица 1

Модельная задача	Название УЧП	Вид УЧП первого 1-го порядка	Тип УЧП первого порядка
О сбросе токсичного вещества в реку	уравнение конвективного переноса		линейное однородное с постоянными коэффициентами
О химической реакции, протекающей в потоке в режиме идеального вытеснения	уравнение химической кинетики		квазилинейное неоднородное с постоянными коэффициентами
О процессе изотермической сорбции газа	уравнение сорбции		линейное неоднородное
	уравнение изотермической сорбции		квазилинейное
О травлении материала (химическом, ионно-лучевом, электронно-лучевом, реактивно-ионном)	уравнение травления материала		нелинейное
О просачивании воды сквозь песок	кинетическое уравнение		квазилинейное однородное
О динамике дорожного движения	кинетическое уравнение		квазилинейное однородное

3. Уравнения характеристик

Рассмотрим оператор

(14)

где заданные непрерывные функции, определенные в некоторой области ;

непрерывно дифференцируемая функция в этой области , причем

Как известно, производная функции в фиксированной точке по направлению единичного вектора равна

Выражение

где можно интерпретировать как производную функции в точке по направлению единичного вектора с компонентами

Ясно, что

Тога оператор , задаваемый формулой (14) можно представить в следующем виде

и рассматривать как производную от функции по направлению вектора умноженную на

Определение 1. Направление, задаваемое вектором называется характеристическим направлением оператора в фиксированной точке .

Определение 2. Кривая , в каждой точке которой ее касательная имеет характеристическое направление оператора , называется характеристикой оператора .

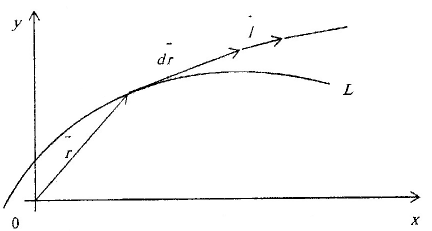
Рисунок 5. Характеристика оператора

В каждой точке характеристики вектор коллинеарен вектору что означает пропорциональность координат этих векторов:

Таким образом, приходим к обыкновенному дифференциальному уравнению характеристик

или (16)

Введя параметр , меняющийся вдоль характеристики, можно записать

,

откуда получаем эквивалентную (16) систему ОДУ в нормальном виде:

(17)

Решив обыкновенное дифференциальное уравнение (16) или нормальную систему обыкновенных дифференциальных уравнений (17), можно найти и построить характеристики везде в той части пространства, где определена дифференцируемая функция , иначе - где задано плоское скалярное поле

Пример 1. Для оператора где дифференциальное уравнение характеристик (16) имеет вид

Разделяя переменные и интегрируя уравнение, получаем

Следовательно, характеристики данного оператора представляют собой однопараметрическое семейство параллельных прямых с угловым коэффициентом , заполняющих собой всю плоскость .

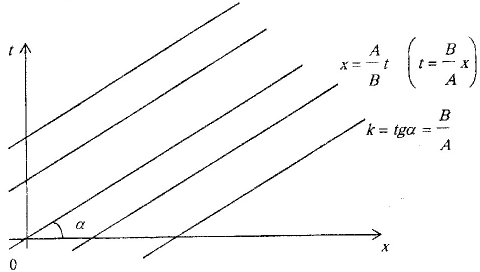
Рисунок 6. Характеристики оператора образуют однопараметрическое