1.3. Модельная задача о процессе изотермической сорбции газа

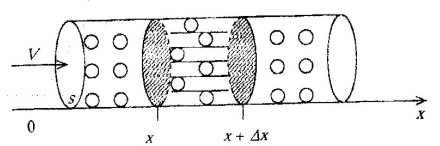
Рисунок 3

Пусть через трубку с постоянной площадью поперечного сечения , заполненную адсорбентом (поглощающим пористым веществом) пропускается газовоздушная смесь – ОВ (отравляющее вещество).

Тепловыделения в трубке бесконечно малы, а температуры потока и адсорбента одинаковы.

Считаем, что скорость потока велика, и процесс диффузии не играет существенной роли в переносе ОВ.

Направим ось вдоль трубки (рис. 3).

Обозначим через:

концентрацию адсорбтива, то есть ОВ, находящегося в газовой фазе, в точке х в момент времени ,

концентрацию адсорбата, то есть ОВ, в адсорбированной фазе, в точке х в момент времени .

Покажем, что концентрация ОВ удовлетворяет уравнению изотермической сорбции газа:

Рассмотрим элементарный слой адсорбента, заключенный между сечениями трубки и .

Составим уравнение материального баланса (УМБ) для этого элементарного слоя за время от до .

УМБ в текстовом виде схематично можно записать так

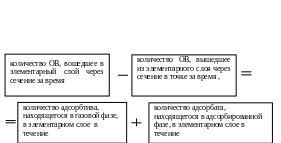
или в формализованном виде:

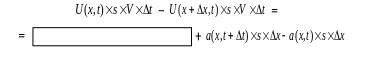
Используя равенство левую часть УМБ можно преобразовать следующим образом:

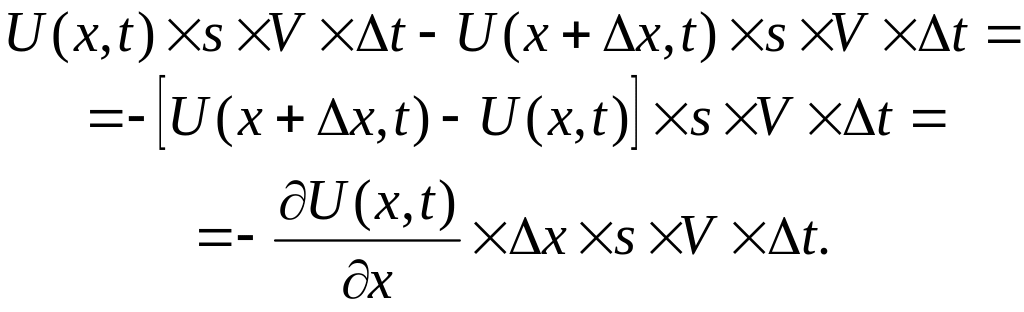
Аналогично правую часть представим так:

Итак,

Отсюда, разделив почленно обе части УМБ на , получим:

И, наконец, приходим к уравнению (3):

Если известна основная кинетическая зависимость где - гладкая функция, то уравнение (3) примет вид:

(4)

где .

Если к УМБ присоединить уравнение кинетики сорбции (изотермы сорбции)

где - кинетический коэффициент,

коэффициент Генри, - непрерывная, не обязательно гладкая функция, то уравнение (3) примет вид:

(5)

где .

1.4. Модельная задача о травлении материала (химическом, ионно-лучевом, электронно-лучевом, реактивно-ионном)

В начальный момент времени имеется некоторый профиль травимого материала. Вследствие процесса травления каждый участок профиля движется в направлении нормали с некоторой скоростью . Выведем уравнение эволюции профиля для двухмерного случая.

На рисунке 4 показаны профили для двух моментов времени: и .

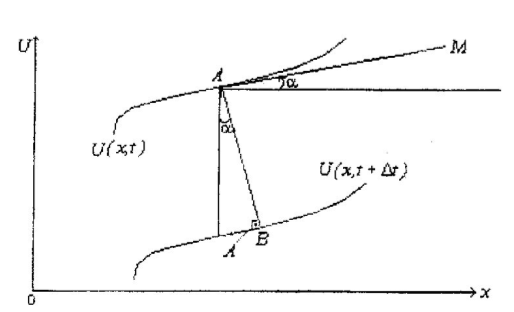
Рисунок 4

Функция описывающая форму профиля, зависит от двух переменных: координаты х и времени .

За время точка А профиля смещается в направлении нормали, на расстояние , которое мало.

Смещение точки А по вертикали за время также мало:

В силу малости можно считать прямоугольным.

Из прямоугольного :

(6)

Угловой коэффициент касательной АМ к исходному профилю травимого материала, задаваемого функцией в точке А, равен:

(7)

Поскольку то учитывая (7),

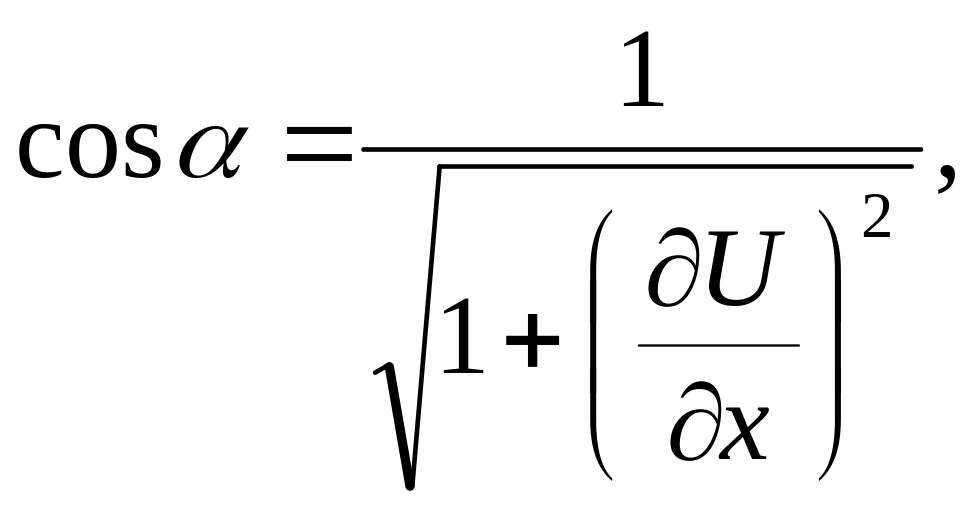
Подставляя в равенство (6) выражения для и , получим

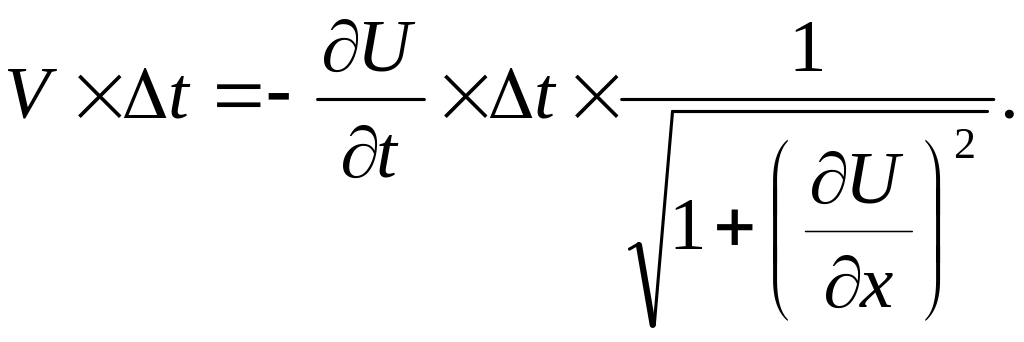
Разделив обе части последнего равенства на , приходим к искомому уравнению травления материала:

(8)

Многообразие процессов, описываемых этим уравнением, связано с различным видом функции V, которая может зависеть от и

В модельных задачах 3 и 4, используя приближенные равенства, мы позволили небезупречный с точки зрения математической строгости переход от уравнений материального баланса (УМБ) к уравнениям в частных производных. Однако при моделировании физико-химических процессов такой нестрогий подход вполне приемлем, поскольку приводит к простым практически полезным моделям.

Математическая строгость изложения приводит к более сложным выкладкам на основе использования понятия и свойств определенного интеграла. Проиллюстрируем это на следующих модельных задачах.