1. Модельные задачи, приводящие к уравнениям с частными производными первого порядка

1.1. Модельная задача о сбросе токсичного вещества в реку

Рисунок 1

Пусть - скорость течения реки. Направим ось вдоль русла реки. Обозначим через расстояние вниз по течению от места сброса вещества. Считаем, что вещество не диффундирует в воде, а переносится течением. Загрязнение реки (концентрация токсичного вещества в воде) будет сначала равно нулю, а затем, поддерживаемое постоянным в точке будет смещаться вниз по течению со скоростью

Обозначим через концентрацию вещества в точке в момент времени . Покажем, что в условиях конвективного переноса, концентрация вещества удовлетворяет так называемому уравнению переноса:

. (1)

Выделим в русле реки элементарный участок длины , ограниченный сечениями в точках и . Обозначив площадь любого произвольного сечения через объем этого элементарного участка можно приближенно считать равным или . Здесь - время от момента до , за которое течение со скоростью переносит вещество на расстояние .

Составим уравнение материального баланса (УМБ) для этого участка реки за время от до .

УМБ, выражающее закон сохранения вещества, в текстовом виде схематично можно записать так:

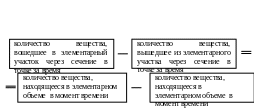
Или:

Разделив почленно обе части УМБ на , получим:

Совершив предельный переход при и , получим уравнение (1):

1.2. Модельная задача о химической реакции, протекающей в потоке в режиме идеального вытеснения

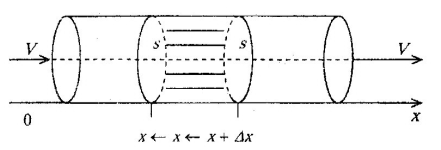
Рисунок 2

Рассмотрим необратимую химическую реакцию первого порядка , протекающую в одномерном потоке (в реакционной трубке) в режиме идеального вытеснения. Здесь - константа скорости реакции задана; скорость потока считаем равной

Направим ось вдоль трубки (рис. 2). Пусть - площадь ее поперечного сечения. При описании такого химического процесса необходимо учитывать не только протекание реакции во времени, но и перемещение вещества вдоль пространственной координаты. Поэтому модельное уравнение динамики этого процесса содержит две независимые переменные: координату и время

Обозначим через:

концентрацию в точке в момент времени непрореагировавшего вещества ,

концентрацию в точке в момент времени образовавшегося вещества (прореагировавшего вещества А). Покажем, что динамика процесса моделируется уравнением химической кинетики:

(2)

Выделим в реакционной трубке (в потоке) элементарный участок длины , ограниченный сечениями в точках и ; его объем - или .

Составим уравнение материального баланса (УМБ) для этого элементарного участка за время от до .

УМБ выражает закон сохранения вещества.

У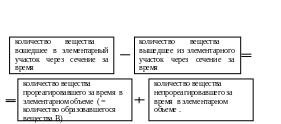 МБ в текстовом виде схематично можно представить так:

или в формализованном виде:

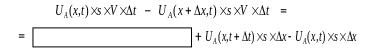
Разделив почленно обе части УМБ на , получим:

Совершив предельный переход при и , приходим к уравнению:

Физический смысл - истинная скорость химической реакции первого порядка, которая равна

Окончательно УМБ принимает вид (2):