Тема: правила диференціювання
ПЛАН:
Похідні елементарних функцій.
Похідні тригонометричних функцій.
Таблиця похідних.
Теореми про похідну суми, добутку і частки функцій.
Похідні елементарних функцій.
Вже доведено, що похідна лінійної функції
y= kx + b дорівнює k, тобто (kx + b)' = k.
Якщо покласти k = 0, b = С, де С – довільна постійна, то С' = 0, тобто похідна постійної функції дорівнює 0.
Якщо у формулі (kx + b)' = k покласти k = 1,
b = 0, то одержимо x' = 1 .
Уже відомо, що (x2)' = 2x .
____________________________________________
Знайдемо похідну функції y = xn , де n є N.
∆y = (x0 + ∆x)n – x0n;
∆y (x0 + ∆x)n – x0n (x0 + ∆x)n – x0n
∆x ∆x (x0 + ∆x) – x0
= (x0 + ∆x)n-1 + (x0 + ∆x)n-2 x0 + (x0 + ∆x)n-3x02 + ...
…+ x0n-1 .
( Скористалися формулою an - bn = ( a - b)( an-1 + an-2 b + an-3b2 + ... + bn-1 )).
f '(x0 ) =
((x0
+
∆x
)n-1
+
x0
+
∆x
)n-2
x0
+ (x0
+
+∆x
)n-3
x02
+...
+ x0n-1)
= ( x0
+ 0)n-1
+ ( x0
+ 0)n-2
x0
+
+(
x0
+ 0)n-3
x02
+
... + x0n-1
=
x0n-1
+
x0
n-1
+ x0
n-1
+ ... …+
x0
n-1
= n x0
n-1
.
Звідси
( xn )' = = n x n-1 , де n є N. (*)
Аналогічно можна знайти похідну функції y = x –n, де n є N:
( x –n )' = -n x –n-1 , де n є N.
Таким чином, для всіх цілих n виконується рівність (*).
____________________________________________
Похідні тригонометричних функцій.
Знайдемо похідну функції y = sin x.
Зафіксуємо x0 і надамо аргументу приросту ∆x, тоді:
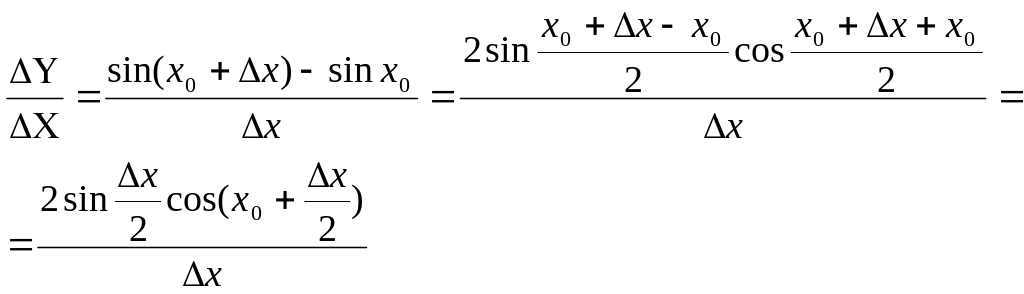
3)
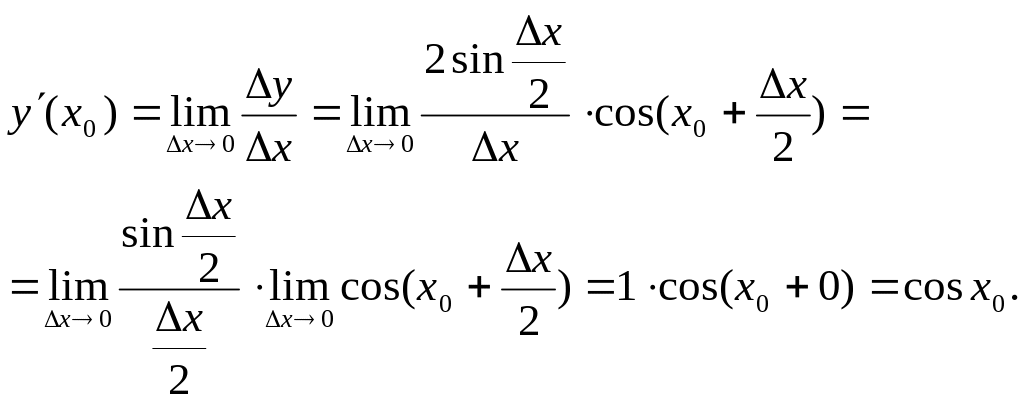
Отже,
Аналогічно можна довести, що
Міркуючи аналогічно, маємо:
;
.
ТАБЛИЦЯ ПОХІДНИХ
(
)
' =
Теореми про похідну суми, добутку і частки функцій.
ТЕОРЕМА 1: Якщо функції f (x) і g (x) диференційовані в
точці x, то їхня сума диференційована в цій
точці і
( f (x) + g (x))' = f ' (x) + g' (x)
або коротко говорять: похідна суми дорівнює
сумі похідних.
ТЕОРЕМА 2: Якщо функції f (x) і g (x) диференційовані в
точці x, то їхній добуток також –
диференційована функція в цій точці і
( f (x) g (x))' = f ' (x) g (x) + f (x) g' (x)
або коротко говорять: похідна добутку двох
функцій дорівнює сумі добутків кожної
функції на похідну другої функції.
ТЕОРЕМА 3: Якщо функції f (x) і g (x) диференційовані в
точці x і g(x) = 0, то частка цих функцій
диференційована в цій точці і
f (x) ' f ' (x) g (x) - f (x) g' (x)
g (x) g2 (x)
Доведення цих теорем знаходиться в підручнику А.М. Колмогорова (п.15, с.117-119)
ТЕМА: Похідна складеної функції.
Розглянемо приклад.
ПРИКЛАД 1: Нехай треба обчислити по заданому значенню x значення функції y, яка задана формулою y = √ 9 – x2 .
Для цього спочатку треба обчислити за заданим значенням x значення u = g (x) = 9 – x2 , а потім за значенням u обчислити y = f (u) = √ u .
Говорять, що функція y є складеною із функцій g і f , і пишуть: y = f ( g (x )).
Функцію g(x) називають внутрішньою функцією, або проміжною змінною, функцію f (u ) – зовнішньою функцією.
Якщо функція g має похідну в точці x0, а функція f – похідну в точці u0 = g(x0), то складена функція y = f ( g (x ))
також має похідну в точці x0 , причому
y ' (x0) = f ' ( g (x0 )) g '(x0).
------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------