
- •1.Статика на площині
- •1.1. Система збіжних сил
- •1.2. Довільна система сил на площині
- •1.3. Розрахунок складених конструкцій. Рівновага сил при наявності тертя ковзання
- •1.4. Розрахунок найпростіших плоских ферм
- •2. Статика в просторі
- •2.1. Система збіжних сил
- •2.2. Зведення довільної просторової системи сил до центра.
- •2.3. Довільна система сил в просторі
- •3. Центр ваги однорідної плоскої фігури
- •Література
- •1.Статика на площині ………………………………………………………….....3
- •1.1. Система збіжних сил…..………………………………………………….3
- •2.1. Система збіжних сил ……………………………………………………25
1.4. Розрахунок найпростіших плоских ферм
1.4.1. Фермою називається геометрично незмінна система, яка складається із стержнів, які з’єднані між собою по кінцях ідеальними шарнірами.
1.4.2. Основна особливість та головна перевага ферм полягає в тому, що всі
її стержні працюють тільки на розтяг або стиск, для цього повинні виконуватись наступні умови: всі стержні ферми прямолінійні; вони з’єднані між собою ідеальними шарнірами; зовнішні сили прикладені тільки в вузлах ферми і діють в її площині; вага стержнів мала порівняно з іншими силами і нею можна знехтувати.
1.4.3. Зробити розрахунок ферми – це значить визначити зусилля в її стержнях, що виникають під дією прикладених до ферми зовнішніх сил, включаючи реакції в′язей. При визначенні реакцій в′язей ферму розглядають в цілому як абсолютно тверде тіло, тоді можна скласти тільки три незалежних рівняння рівноваги: отже опорних реакцій повинно бути не більше трьох.
1.4.4. Якщо вся ферма під дією зовнішніх сил перебуває в рівновазі, то і кожний вузол її перебуває також в рівновазі. На вирізаний (подумки) вузол діють зовнішні сили та реакції стержнів, які напрямлені вздовж їх осей (вони виражають собою дію відкинутої частини ферми на вирізаний вузол). Всі ці сили утворюють плоску збіжну систему сил (п.1.1.1), для якої складають два рівняння рівноваги (1.2). Таким чином розрахунок ферм методом вирізання вузлів треба починати з вузла, в якому перетинаються тільки два стержні, а в кожному наступному вузлі має бути не більше двох невідомих зусиль, які завжди напрямляємо від вузла: відповідь зі знаком „+” свідчить про те, що стержень дійсно розтягується, а знак ” – ” вказує на те, що стержень стискається.
Шляхом переходу від вузла до вузла визначають зусилля в усіх стержнях ферми методом послідовного вирізання вузлів.
1.4.5. Останній вузол при розрахунку ферми методом послідовного вирізання вузлів є перевірочним.
1.4.6. Спосіб наскрізних перерізів (спосіб Ріттера) застосовується для визначення зусиль в окремих стержнях ферми. Ідея способу полягає в складанні рівнянь рівноваги, кожне з яких містить в собі лише одне невідоме. Перш ніж знаходити зусилля необхідно майже завжди знайти реакції опор.
1.4.7. Щоб визначити зусилля в будь-якому зі стержнів ферми, її перерізують подумки на дві частини (наскрізь), причому переріз повинен обов′язково проходити через стержень, в якому визначається зусилля. Переріз проводять таким чином, щоб осі всіх перерізаних стержнів або їх продовження (крім стержня, в якому шукаємо зусилля) перетинались в одній точці, яка називається моментною або точкою Ріттера. Це означає, що якщо переріз проходить через n стержнів, то осі n-1 стержня мають перетнутися в одній точці.
Частину ферми, до якої прикладено більше сил, відкидають та її дію на іншу частину ферми замінюють невідомими реакціями перерізаних стержнів, вважаючи, що стержні розтягнуті. Оскільки розглядувана частина ферми перебуває в рівновазі під дією плоскої довільної системи сил, то можна скласти три незалежних рівняння рівноваги максимум відносно трьох моментних точок. Таким чином, з одного перерізу можна визначити не більше трьох зусиль. Найпростіше розв′язання отримують, якщо переріз проходить через три стержні, які не перетинаються в одній точці: точка перетину осей двох стержнів є моментною для третього стержня.
1.4.8. Якщо два з перерізаних стержнів паралельні, то моментна точка для третього стержня знаходиться в нескінченості і в цьому випадку складають рівняння проекцій всіх сил, що діють на розглядувану частину ферми, на вісь, яка перпендикулярна до напряму паралельних стержнів.
Приклад 1.8. Визначити зусилля в усіх стержнях ферми (рис. 1.16,а) методом послідовного вирізання вузлів, якщо F = 50 кН, d = 3 м, h = 4 м, = 45о. Розв′язання. Ферма (рис. 1.16,а) складається з шести вузлів (n = 6), дев′яти стержнів (k = 9) і умова статичної означуваності ферми k = 2n – 3 виконується.
Пронумеруємо вузли ферми від 1 до 6 (рис. 1.16,а). На ферму накладені в′язі у вигляді шарнірно-рухомої опори В (реакція RB напрямлена перпендикулярно до горизонтальної поверхні, по якій може рухатись опора) та шарнірно-нерухома опора А (напрям реакції RA заздалегідь невідомий: представляємо її двома складовими XA та YA).
Визначимо
складові реакцій опор А та В (рис.1.16, а).
Для зручності силу F
розкладаємо на складові:
![]() (кН);
(кН);
![]() .
Розглянемо рівновагу ферми як абсолютно
твердого тіла. На неї діє плоска довільна
система сил, незалежних рівнянь три:
.
Розглянемо рівновагу ферми як абсолютно
твердого тіла. На неї діє плоска довільна
система сил, незалежних рівнянь три:
![]()
![]() ;
;
![]()
![]() ;
;
![]()
![]() ;
;
звідси
![]() (кН);
(кН);
![]() (кН);
(кН);
![]() (кН);
(кН);
Перевірка:
![]() .
.
Реакції визначено правильно.
Визначимо зусилля в стержнях ферми (рис.1.16) методом послідовного вирізання вузлів.
Розрахунок
проведено в табличній формі (табл. 1.1).
Починати треба з вузла 1 або 6 (див. п.
1.4.4). Порядок вирізання вузлів, наприклад,
6, 1, 2, 5, 3, 4 (перевірочний) або 6, 5, 4, 1, 2, 3
(перевірочний). Існують і інші варіанти.
В табл. 1.1 використані кути
![]() та
та![]() (рис. 1.16,а), які обчислимо:
(рис. 1.16,а), які обчислимо:
![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
;
![]() .
.
П
![]() еревіримо
правильність знаходження зусиль
еревіримо
правильність знаходження зусиль
![]() для ферми (рис.1.16, а) методом наскрізних
перерізів.
для ферми (рис.1.16, а) методом наскрізних
перерізів.
Проведемо спочатку переріз І-І через стержні 3 – 5, 4 – 5, 4 – 6 (рис.1.16,а), пам′ятаючи, що найпростіше розв′язання отримаємо в випадку, коли переріз проходить через три стержні, осі яких не перетинаються в одній точці. Розглянемо верхню частину ферми (рис. 1.16,б), яка менш завантажена. Дію нижньої частини на верхню заміняємо реакціями стержнів, вважаючи, що стержні розтягнуті.
Для
знаходження зусилля
![]() беремо суму моментів всіх сил, що
беремо суму моментів всіх сил, що
діють на верхню частину ферми, відносно точки 4 (там перетинаються осі
двох інших перерізаних стержнів):
![]() ;
;
![]() ,
,
звідси
![]() (кН);
(кН);
Визначаємо
зусилля в
![]() :
моментна точка в цьому випадку збігається
з вузлом 5, в якому перетинаються два
інших перерізаних стержня (5 – 3 та 4 –
5). Маємо:
:
моментна точка в цьому випадку збігається
з вузлом 5, в якому перетинаються два
інших перерізаних стержня (5 – 3 та 4 –
5). Маємо:
![]() ;
;
![]() ,
,
звідси
![]() (кН);
(кН);
Для
знаходження
![]() треба взяти моментну точку на перетині
осей стержнів 5–3 та 6 – 4, але ці стержні
паралельні між собою, тому моментна
точка лежить у нескінченості. У цьому
випадку спроектуємо всі сили, що діють
на верхню частину ферми (рис. 1.16,б) на
вісь Х,
яка
перпендикулярна до паралельних стержнів:
треба взяти моментну точку на перетині
осей стержнів 5–3 та 6 – 4, але ці стержні
паралельні між собою, тому моментна
точка лежить у нескінченості. У цьому
випадку спроектуємо всі сили, що діють
на верхню частину ферми (рис. 1.16,б) на
вісь Х,
яка
перпендикулярна до паралельних стержнів:
Таблиця 1.1
Вузол |
Схема вузла |
Рівняння рівноваги. Відповідь* (кН) |
|
2 |
3 |
6 |
|
S6-4, S6-5 - ?
S6-5=35.35, S6-4=-35.35
|
1 |
|
S1-3, S1-2 - ?
S1-3=24.74, S1-2=20.61
|
2 |
|
S2-3, S2-4 - ?
S2-3=49.45, S2-4=-130.2 |
*Студенти подають розрахунки повністю.
1 |
2 |
3 |
5 |
|
S5-3, S5-4 - ?
S5-4=-58.92, S5-3=47.13 |
3 |
|
S3-4 - ?
Звідси, S3-4 =-26.37
|
4 |
Перевірочний вузол |
|
|
|
|
Задача розв’язана правильно |
||
![]() ;
;
![]() ,
,
звідси
![]() (кН);
(кН);
Для визначення зусилля в стержні 1 – 2 проводимо переріз ІІ-ІІ (рис.1.16,а) і розглядаємо рівновагу лівої частини (рис.1.16,в). Моментна точка збігається з вузлом 3, бо в ньому перетинаються всі розрізані стержні крім шуканого. Маємо:
![]() ;
;
![]() ,
,
звідси
![]() (кН).
(кН).
Як бачимо, всі результати практично збігаються з обчисленими раніше способом вирізання вузлів (див табл. 1.1).


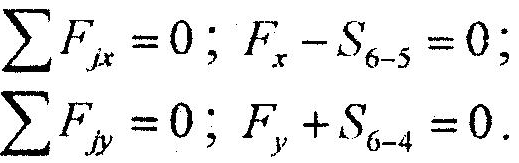 ,
звідси
,
звідси

 ,
звідси
,
звідси


