
- •Часть 1 Занятие 1. Тема: «Двойной интеграл. Повторное интегрирование».
- •3. В аудитории.
- •4. Задачи для самостоятельной работы.
- •Занятие 2. Тема: «Замена переменной в двойном интеграле».
- •2. В аудитории.
- •3. Задачи для самостоятельной работы.
- •Занятие 3. Тема: «Приложение двойного интеграла».
- •1. Геометрические приложения двойных интегралов.
- •3. В аудитории.
- •4. Задачи для самостоятельной работы.
- •Занятие 4. Тема: «Тройной интеграл».
- •4. В аудитории.
- •4. Задачи для самостоятельной работы.
- •Занятие 5. Тема: «Криволинейный интеграл 1-го рода, приложения».
- •3. В аудитории.
- •4. Задачи для самостоятельной работы.
- •Занятие 6. Тема: «Криволинейный интеграл 2-го рода, формула Грина, приложения».
- •2. Вычисление криволинейного интеграла 2-го рода с помощью определенного интеграла.
- •3. Связь между криволинейными интегралами 1-го и 2-го рода.
- •4. Формула Грина.
- •5. Условия независимости криволинейного интеграла 2-го рода от пути интегрирования.
- •5. В аудитории.
- •6. Задачи для самостоятельной работы.
- •Занятия 7-8 (дополнителные). Тема: «Поверхностный интеграл, формулы Стокса, Остроградского - Гаусса».
- •2. Поверхностные интегралы 1-го рода.
- •6. В аудитории.
- •7. Задачи для самостоятельной работы.
- •Часть 2
- •2 Вариант
- •3 Вариант
- •4 Вариант
- •Уровень б
- •5 Вариант
Занятия 7-8 (дополнителные). Тема: «Поверхностный интеграл, формулы Стокса, Остроградского - Гаусса».
1.
Простые поверхности.
Функция
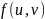 называется непрерывно дифференцируемой
на замкнутом множестве
называется непрерывно дифференцируемой
на замкнутом множестве
 ,
если она определена и имеет частные
производные
,
если она определена и имеет частные
производные
 на открытом множестве
на открытом множестве
 ,
содержащем замкнутое множество
.
,
содержащем замкнутое множество
.
Пусть
- ограниченная область в
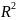 ,
функции
,
функции
 непрерывно дифференцируемы на замкнутом
множестве
непрерывно дифференцируемы на замкнутом
множестве
 ,
где
,
где
 – граница области
.
Тогда отображение
– граница области
.
Тогда отображение
 :
:
 ,
определяемое формулами
,
определяемое формулами
 (6.1)
(6.1)
называется
непрерывно
дифференцируемым.
Если при этом в каждой точке
 ранг функциональной матрицы
ранг функциональной матрицы

равен двум, то отображение : называется гладким.
Если
 - замкнутое ограниченное множество в
;
:
есть такое гладкое отображение, что
соответствие между множествами
и
- замкнутое ограниченное множество в
;
:
есть такое гладкое отображение, что
соответствие между множествами
и
 является взаимно однозначным, то
множество
является взаимно однозначным, то
множество
 называется простой
поверхностью
в
называется простой
поверхностью
в
 ,
а уравнения (6.1) называются параметрическими
уравнениями
простой поверхности
.
,
а уравнения (6.1) называются параметрическими
уравнениями
простой поверхности
.
Уравнения (6.1) простой поверхности можно записать в векторной форме:
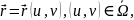
 . (6.2)
. (6.2)
Пусть
есть простая поверхность, заданная
уравнением (6.1) или векторным уравнением
(6.2). Рассмотрим точку
 на поверхности
,
где
- внутренняя точка области
.
Построим координатные линии
на поверхности
,
где
- внутренняя точка области
.
Построим координатные линии
 и
и
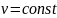 ,
проходящие через точку
.
Векторы
,
проходящие через точку
.
Векторы

 (6.3) будут касательными к соответствующим
координатным линиям (
(6.3) будут касательными к соответствующим
координатным линиям ( ).
).
На простой гладкой поверхности всегда определено непрерывное поле единичных нормальных векторов
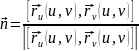 .
(6.4)
.
(6.4)
(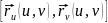 - векторное произведение векторов
- векторное произведение векторов
 и
и
 )
)
Произвольные гладкие поверхности могут быть как ориентируемыми (двусторонними), так и неориентируемыми (односторонними). Гладкая поверхность, являющаяся границей области в , ориентируема. Ее внутренняя сторона задается нормальными векторами, направленными внутрь области (внутренними нормалями), внешняя сторона определяется внешними нормалями. Для построения поля внутренних нормалей к границе области достаточно построить внутреннюю нормаль к какой-то одной точке границы.
Рассмотрим
 ,
,
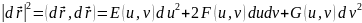 ,
(6.5) где
,
(6.5) где
 .
(6.6)
.
(6.6)
Выражение,
стоящее в правой части (6.5), называется
первой
квадратичной формой поверхности,
числа
 называются коэффициентами первой
квадратичной формы. В любой точке простой
поверхности
называются коэффициентами первой
квадратичной формы. В любой точке простой
поверхности
 .
.
Площадь простой поверхности определяется следующим образом (область предполагается измеримой по Жордану):
 . (6.7)
. (6.7)
Для поверхности, являющейся графиком непрерывно дифференцируемой функции на замыкании измеримой по Жордану области , формула (6.7) для площади поверхности имеет вид (см. занятие 3):
 .
(6.8)
.
(6.8)
2. Поверхностные интегралы 1-го рода.
Определение
6.1
Пусть
- простая поверхность, заданная векторным
уравнением (6.2). Пусть на поверхности
определена непрерывная функция
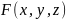 .
Двойной интеграл
.
Двойной интеграл

называется
поверхностным
интегралом 1-го рода
от функции
по поверхности
и обозначается
 .
Таким образом, по определению
.
Таким образом, по определению
 . (6.9)
. (6.9)
Интеграл
(6.9) не зависит от выбора параметрического
уравнения поверхности. Аддитивность
интеграла (6.9) относительно поверхности
следует из аддитивности двойного
интеграла по области интегрирования.
Подставляя выражение
 через коэффициенты первой квадратичной
формы поверхности в (6.9), получим следующее
выражение для поверхностного интеграла
1-го рода:
через коэффициенты первой квадратичной
формы поверхности в (6.9), получим следующее
выражение для поверхностного интеграла
1-го рода:
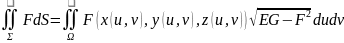 .
(6.10)
.
(6.10)
Если поверхность является графиком непрерывно дифференцируемой функции на замыкании измеримой по Жордану области , то имеет место равенство
 .
(6.11)
.
(6.11)
Пример
6.1
Вычислить поверхностный интеграл 1-го
рода
 ,
где
- часть гиперболического параболоида
,
вырезанная цилиндром
.
,
где
- часть гиперболического параболоида
,
вырезанная цилиндром
.
∆ По формуле (6.11) получим
 ,
где
- круг
,
где
- круг
 .
Переходя к полярным координатам
и сводя двойной интеграл к повторному,
найдем
.
Переходя к полярным координатам
и сводя двойной интеграл к повторному,
найдем
 .∆
.∆
Пример 6.2 Вычислить поверхностный интеграл 1-го рода , где – верхняя полусфера .
∆ Параметризуем полусферу
 ,
,
 .
.
Вычислим коэффициенты первой квадратичной формы поверхности и применим формулу (6.10). Получим:
 ,
,
 ,
,
 .
.
 ,
,
 ,
,
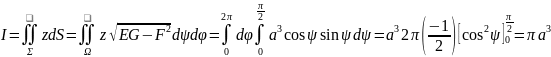 .
∆
.
∆
Пример
6.3
Вычислить интеграл
 ,
где
- часть цилиндрической поверхности
,
где
- часть цилиндрической поверхности
 .
.
∆ Применим
формулу (6.10). Вычислим коэффициенты
квадратичной формы для цилиндрических
координат:
 .
Поэтому
.
Поэтому
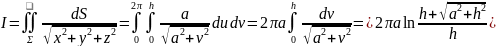 .
∆
.
∆
Пример
6.4
Вычислить интеграл
 ,
где
- полная поверхность конуса
,
где
- полная поверхность конуса
 .
.
∆ Пусть
 - боковая поверхность конуса,
- боковая поверхность конуса,
 - его основание; тогда:
- его основание; тогда:
 .
.
К первому интегралу применим формулу (6.11). На боковой поверхности конуса
 ,
,
 .
.
Следовательно,
 .
.
На
основании конуса
 ,
поэтому второй интеграл равен четыре
площади основания конуса
,
поэтому второй интеграл равен четыре
площади основания конуса
 .
Итак,
.
Итак,
 .
∆
.
∆
3. Поверхностные интегралы 2-го рода. Пусть в некоторой окрестности простой поверхности задано непрерывное векторное поле, т.е. определена вектор – функция
 ,
(6.12) компоненты
,
(6.12) компоненты
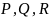 которой есть непрерывные функции в
некоторой области, содержащей поверхность
.
которой есть непрерывные функции в
некоторой области, содержащей поверхность
.
Ориентируем поверхность единичными нормалями
 .
(6.13)
.
(6.13)
Противоположная
ориентация поверхности
возникает при замене в формуле (6.12)
вектора
 на вектор
на вектор
 .
Для простой поверхности
.
Для простой поверхности
 .
.
Спроектируем
в каждой точке поверхности
вектор
 на нормальный вектор. Тогда на поверхности
будет определена непрерывная функция
на нормальный вектор. Тогда на поверхности
будет определена непрерывная функция
 ,
знак которой зависит от ориентации
поверхности.
,
знак которой зависит от ориентации
поверхности.
Определение 5.2 Поверхностный интеграл 1-го рода
 (6.14) называется потоком
вектор–функции
через ориентированную поверхность
или поверхностным
интегралом 2-го рода.
(6.14) называется потоком
вектор–функции
через ориентированную поверхность
или поверхностным
интегралом 2-го рода.
Очевидно, при изменении ориентации поверхности на противоположную интеграл (6.14) меняет знак.
Для поверхностного интеграла 2-го рода используются еще и следующие обозначения:
=
(6.15)
Воспользовавшись
формулой (6.9) для вычисления интеграла
(6.14), выразим поток векторного поля
через простую поверхность
,
ориентированную нормалями (6.13), при
помощи двойного интеграла по плоской
области от смешанного произведения
трех векторов
 :
:
 =
=
 .
(6.16)
.
(6.16)
Пример
6.5
Вычислить поверхностный интеграл
 по внешней стороне полусферы
по внешней стороне полусферы
 (внешняя сторона определяется нормалями,
направленными от центра).
(внешняя сторона определяется нормалями,
направленными от центра).
∆ Вектор
имеет координаты (см. формулу (6.15))
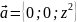 .
Вектор нормали к поверхности
.
Вектор нормали к поверхности
 коллинеарен градиенту функции
:
коллинеарен градиенту функции
:
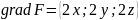 .
Внешняя сторона полусферы в данном
случае определяется нормалями,
составляющими острый угол с осью
.
Внешняя сторона полусферы в данном
случае определяется нормалями,
составляющими острый угол с осью
 .
Единичный вектор к внешней стороне
полусферы радиуса 1 имеет координаты:
.
Единичный вектор к внешней стороне
полусферы радиуса 1 имеет координаты:
 .
Следовательно,
.
Следовательно,
 и
и
 .
.
Полусферу можно задать как график функции
 .
.
От поверхностного интеграла 1-го рода перейдем к кратному, воспользовавшись формулой (6.11):
 ,
,
 ∆
∆
Пример
6.6
Вычислить поверхностный интеграл
 по внешней стороне конической поверхности
по внешней стороне конической поверхности
 , считая, что внешняя сторона определяется
нормалями, составляющими с осью
тупой угол.
, считая, что внешняя сторона определяется
нормалями, составляющими с осью
тупой угол.
∆ Перепишем
уравнение поверхности конуса в виде:
или
 .
Отсюда
.
Отсюда
 .
Выберем направление нормали: проекция
на ось
должна быть меньше нуля. Единичная
нормаль имеет координаты:
.
Выберем направление нормали: проекция
на ось
должна быть меньше нуля. Единичная
нормаль имеет координаты:
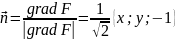 .
Следовательно,
.
Следовательно,
 и
и
 .
∆
.
∆
Пример
6.7
Вычислить поток вектора
 через внутреннюю поверхность конической
поверхности
.
через внутреннюю поверхность конической
поверхности
.
∆ Поверхность конуса можно параметризовать следующим образом:
 ,
,
 ,
,
 .
.
Воспользовавшись формулой (6.16), получим:
 .
.
Заметим,
что при выбранной параметризации
поверхности для проекции нормального
вектора
 на ось
справедливо неравенство
на ось
справедливо неравенство
 ,
поэтому вектор нормали
,
поэтому вектор нормали
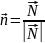 составляет с осью
острый угол и вектор
составляет с осью
острый угол и вектор
 определяет внутреннюю сторону конической
поверхности. ∆
определяет внутреннюю сторону конической
поверхности. ∆
4.
Формула Стокса.
- непрерывно дифференцируемое векторное
поле, заданное в некоторой области,
содержащей простую ориентированную
поверхность
.
 - замкнутый соответственно ориентированный
контур, ограничивающий поверхность
(поверхность
натянута на контур
).
Говорят, что поверхность и ограничивающий
ее контур ориентированы соответственно,
если наблюдатель, движущийся по контуру
и смотрящий на поверхность с той стороны,
куда направлена нормаль к поверхности,
видит поверхность слева. Тогда имеет
место формула Стокса:
- замкнутый соответственно ориентированный
контур, ограничивающий поверхность
(поверхность
натянута на контур
).
Говорят, что поверхность и ограничивающий
ее контур ориентированы соответственно,
если наблюдатель, движущийся по контуру
и смотрящий на поверхность с той стороны,
куда направлена нормаль к поверхности,
видит поверхность слева. Тогда имеет
место формула Стокса:

Эта формула может быть переписана в виде:

или
 ,
(6.17)
,
(6.17)
где
 - вектор единичной нормали к поверхности
,
направленный соответственно направлению
контура
.
- вектор единичной нормали к поверхности
,
направленный соответственно направлению
контура
.
Формула Стокса может быть записана в векторной форме: циркуляция векторного поля по контуру равна потоку вихря этого поля через поверхность , натянутого на контур , т.е.
 ,
,
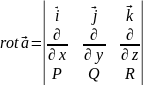 .
(6.18)
.
(6.18)
Пример
6.8
Вычислить интеграл
 ,
где
- кривая пересечения параболоида
,
где
- кривая пересечения параболоида
 с плоскостью
с плоскостью
 ,
ориентированная положительно относительно
вектора
,
ориентированная положительно относительно
вектора
 .
.
∆ Применим
формулу Стокса. За поверхность
,
ограниченную кривой
,
примем часть секущей плоскости
,
лежащей внутри параболоида. Единичным
вектором нормали к
,
направленным соответственно направлению
кривой
,
является вектор
 .
.
Так
как
 ,
то
,
то
 .
.
Применяя формулу (6.17), получим
 .
.
Так
как
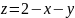 на поверхности
,
то
на поверхности
,
то
 .
Следовательно,
.
Следовательно,
 ,
,
где Ω – проекция на плоскость . Исключая из уравнений
 ,
,
получим
 ,
,
т.е.
Ω
– есть круг радиуса
 .
Следовательно,
.
Следовательно,
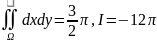 .∆
.∆
Пример
6.9
Вычислить криволинейный интеграл
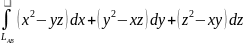 ,
взятый по отрезку винтовой линии
,
взятый по отрезку винтовой линии
 (рис. 6.1) от точки
(рис. 6.1) от точки
 до точки
до точки
 .
.




Рис. 6.1
∆ Дополним
кривую
 отрезком
отрезком
 до замкнутой кривой
.
В силу аддитивности криволинейного
интеграла относительно кривой
до замкнутой кривой
.
В силу аддитивности криволинейного
интеграла относительно кривой

 .
.
Так
как на отрезке
выполнены равенства
 ,
то
,
то
 .
.
Рассмотрим
векторное поле:
 .
Вычислим (6.18)
.
Вычислим (6.18)
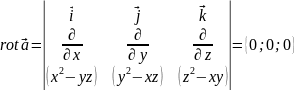 .
.
По
формуле Стокса (6.18) ,
следовательно,
,
следовательно,
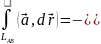
 .
∆
.
∆
5.
Формула Остроградского.
Пусть
 - ограниченная область, граница которой
есть кусочно гладкая поверхность,
ориентированная внешними нормалями. В
задано непрерывно дифференцируемое
векторное поле
.
Тогда поток векторного поля
через границу области
равен тройному интегралу от
- ограниченная область, граница которой
есть кусочно гладкая поверхность,
ориентированная внешними нормалями. В
задано непрерывно дифференцируемое
векторное поле
.
Тогда поток векторного поля
через границу области
равен тройному интегралу от
 по области
,
т.е.
по области
,
т.е.
 ,
(6.19) или
,
(6.19) или
 .
(6.20)
.
(6.20)
Пример
6.10
Показать, что поверхностный интеграл
 по внешней стороне части конической
поверхности
по внешней стороне части конической
поверхности
 равен нулю.
равен нулю.
∆ Запишем
поверхностный интеграл в виде
,
где
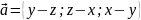 .
Тогда
.
Тогда
 .
Применим формулу Остроградского к
области
,
изображенной на рис. 6.2.
.
Применим формулу Остроградского к
области
,
изображенной на рис. 6.2.



Рис. 6.2
Граница
состоит из поверхности
и круга
радиуса
с центром в точке
 .
Так как
,
то
.
Так как
,
то
 .
.
Следовательно,
 .
∆
.
∆
Пример
6.11
Вычислить поверхностный интеграл
 по внешней стороне полной поверхности
конуса
по внешней стороне полной поверхности
конуса
 .
.
∆ Запишем
поверхностный интеграл в виде
,
где
 .
Тогда
.
Тогда
 .
Применим формулу Остроградского:
.
Применим формулу Остроградского:
 ,
,
где
 – объем конуса, площадь основания
которого круг радиуса 4, высотой 4.
Следовательно,
– объем конуса, площадь основания
которого круг радиуса 4, высотой 4.
Следовательно,
 .∆
.∆
