2. В аудитории.

1. В двойном интеграле перейти к полярным координатам, расставить пределы интегрирования, где - параболический сегмент (Д. 3941).

2. Перейти к полярным координатам, расставить пределы интегрирования в том и другом порядке:

2.1 (Д. 3944);

2.2 ;

2.3 , где область ограничена кривой (Д.3947).

3. Поменять порядок интегрирования (Д. 3948).

4. Перейдя к полярным координатам, заменить двойной интеграл однократным , где (Д. 3952).

5. Перейдя к полярным координатам, вычислить:

5.1 , где ;

5.2 ;

6. Перейти к новым переменным в интеграле:

6.1 , если ;

6.2 , если .

7. Вычислить двойные интегралы и , вводя обобщенные полярные координаты, где область ограничена астроидой .

8. Вычислить:

8.1 , где область ограничена кривой (Д.3965);

8.2 , где область ограничена кривыми (Д.3970)

3. Задачи для самостоятельной работы.

1. В двойном интеграле перейти к полярным координатам, расставить пределы интегрирования, где - треугольник (Д. 3940).

2. Перейти к полярным координатам, расставить пределы интегрирования в том и другом порядке:

2.1 (Д. 3943);

2.2 (Д. 3945);

2.3 (Д. 3946).

3. Поменять порядок интегрирования (Д. 3949).

4. Перейдя к полярным координатам, заменить двойной интеграл однократным , где (Д. 3953).

5. Перейдя к полярным координатам, вычислить:

5.1 ;

5.2 ;

5.3 .

6. Перейти к новым переменным в интеграле , где область ограничена кривыми , если (Д.3959).

7. Найдите замену переменных , при которой область , ограниченная кривыми , является образом прямоугольника, стороны которого параллельны осям координат на плоскости .

8. Вычислить:

8.1 , где область ограничена эллипсом (Д.3967);

8.2 , где область ограничена кривыми (Д.3969)

Занятие 3. Тема: «Приложение двойного интеграла».

1. Геометрические приложения двойных интегралов.

А) Площадь измеримого по Жордану множества на плоскости выражается формулой

. (3.1)

Если - криволинейная трапеция, то, сведя двойной интеграл (3.1) к повторному, придем к известному выражению площади криволинейной трапеции с помощью определенного интеграла

.

Переходя в (3.1) к новым переменным по формулам (2.1), получим выражение площади области в криволинейных координатах

. (3.2)

Величину , представляющую собой площадь прямоугольника со сторонами и , естественно назвать элементом площади в прямоугольных координатах и , а величину - элементом площади в криволинейных координатах и . Модуль якобиана представляет собой коэффициент растяжения площади в точке при отображении области плоскости на область плоскости .

Если – криволинейный сектор на плоскости , ограниченный лучами и кривой , где и - полярные координаты (рис. 3.1), то переходя в формуле к полярным координатам, учитывая, что , а , и сводя двойной интеграл к повторному, получаем известное выражение площади криволинейного сектора через определенный интеграл

.

Рис. 3.1

Б) Объем тела (рис. 3.2), где – измеримый компакт, а - непрерывная неотрицательная в области функция, выражается формулой

. (3.3)

Рис. 3.2

В) Пусть функция определена и имеет непрерывные частные производные в некоторой области , содержащей . Тогда площадь поверхности (рис. 3.2) выражается интегралом , (3.4)

где - проекция данной поверхности на плоскость .

2. Физические приложения двойных интегралов. Пусть - материальная бесконечно тонкая пластинка (измеримый компакт на плоскости ) с плотностью . Тогда справедливы следующие формулы:

А) – масса пластинки; (3.5)

Б) – статические моменты инерции относительно осей и ;

В) – координаты центра тяжести пластинки;

Г) – моменты инерции относительно осей и ;

Д) – момент инерции пластинки относительно начала координат.

Пример 3.1 Найти площадь области , ограниченной кривыми: .

∆ Область изображена на рис 3.3.

Рис. 3.3

Разрешим относительно . Применим формулу (3.1) и сведем двойной интеграл к повторному, выбрав порядок интегрирования,

. ∆

Пример 3.2 Найти площадь области , ограниченной кривыми: .

∆ Область изображена на рис 3.4.

Рис. 3.4

Применим формулу (3.1), сведем двойной интеграл к повторному. Для этого найдем точки пересечения кривых : . Расставим пределы интегрирования:

.∆

Пример 3.3 Найти площадь области , ограниченной кривыми:

.

∆ Перепишем уравнения кривых в виде:

.

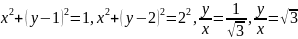Область изображена на рис 3.5.

Рис. 3.5

Применим формулу (3.1), перейдем к полярным координатам: . Уравнения кривых в полярных координатах, соответственно, примут вид:

.

Вычислим площадь, перейдя к полярным координатам:

. ∆

Пример 3.4 Найти объем тела , ограниченного поверхностями .

∆ Данное тело можно представить в виде , где - область на плоскости , ограниченная кривыми , т.е. . Применяя формулу (3.3) и сводя двойной интеграл к повторному, получим

. ∆

Пример 3.5 Найти объем тела , ограниченного поверхностями .

∆ Данное тело можно представить в виде , где - область на плоскости , ограниченна кривой . Кривая представляет собой окружность радиуса 1, с центром в точке . Следовательно, . Применим формулу (3.3)

.

Перейдем к полярным координатам с центром в точке

.

Уравнение окружности в указанных координатах имеет вид . Следовательно,

. ∆

Пример 3.6 Найти площадь поверхности части полусферы , заключенной внутри цилиндра .

∆ Применим формулу (3.4). Учтем, что

.

Следовательно,

, где .

Перейдем к полярным координатам , сведем двойной интеграл к повторному

.∆

Пример 3.7 Пластинка задана неравенствами - поверхностная плотность. Найти массу пластинки.

∆ Согласно формуле (3.5), масса пластинки равна , где пластинка изображена на рис. 3.6.

Рис. 3.6

Сделаем эллиптическую замену: . При этом , следовательно, и . Якобиан преобразования равен . Перейдем к повторному интегралу, масса пластинки равна

. ∆